В настоящее время наибольшее место в экономической науке занимают вопросы, связанные с влиянием ментальных свойств хозяйствующих субъектов на функционирование экономической системы. То, что думают экономические агенты о рынках, на которых работают, то, какие ожидания они закладывают в свои хозяйственные программы, то, насколько длительные и оптимистичные планы они строят, оказывает решающее значение на их текущие действия и, следовательно, на последующую эволюцию всей национальной и мировой экономики. Можно сказать, что представления хозяйственных участников о будущем формируют само это будущее.

В последние годы в число наиболее актуальных и важных выдвинулись вопросы, связанные с функционированием отраслевых рынков. Это связано с вхождением мировой экономики в новую фазу развития – фазу перманентного генерирования всевозможных инноваций. Подобные инновации ведут не только к радикальной трансформации уже существующих отраслевых и продуктовых рынков, но и к возникновению принципиально новых рыночных сегментов, а порой, наоборот, к полному отмиранию традиционных направлений производства товаров и услуг. В этой связи все вопросы, связанные с изучением закономерностей процесса принятия решений о внедрении экономических новшеств, приобретают особую актуальность и значимость. В данной статье мы рассмотрим вопрос о влиянии величины дисконта на инвестиционные и инновационные решения предпринимателей.

Дисконт и экспектации как факторы процедуры принятия инновационных решений предприятий

Процесс принятия решений экономических субъектов о переходе к новому хозяйственному укладу ранее довольно подробно рассматривался в предыдущих работах автора [1]. В последней публикации, посвященной данной группе вопросов, был получен принципиальный результат о влиянии дисконта на поведение экономических агентов на стадии выработки решения о принятии инновации. Данный результат был оформлен в виде теоремы о влиянии дисконта на инновации. Однако в выполненных построениях был недоучтен временной фактор. Кроме того, за бортом рассмотрения оказался режим, когда величина дисконта выше темпа экономического роста. Снятие указанных ограничений требует уточнения всех аналитических конструкций и содержательных выводов, что и является непосредственной задачей данного раздела.

Рассмотрим процесс принятия решения менеджментом компании о переходе ее на новые методы производственной деятельности. При этом в соответствии с традициями теории технологических ловушек будем рассматривать только два состояния системы: либо инновация принимается, либо она отвергается; никаких промежуточных или компромиссных решений не предполагается. Основополагающим понятием для выбранного нами формата исследования является экономический эффект (E₀) от внедрения планируемой инновации, который может быть представлен следующим образом:

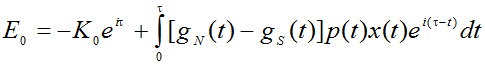                (1)

где x(t) – общий объем производства и реализации фирмы (в физическом выражении или в сопоставимых ценах); p(t) – цена единицы выпускаемой компанией продукции; g_S – норма прибыли производства продукции, соответствующая старому хозяйственному укладу; g_N – норма прибыли производства продукции, соответствующая новому хозяйственному укладу; К₀ – капитальные издержки, необходимые для перехода к новому хозяйственному укладу (например, для закупки нового оборудования и осуществления перехода от старой технологии к новой); t – время (год); 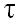– период времени, в течение которого фирма предполагает вести зозяйственную деятельность и окупить произведенные капитальные издержки; i – ставка дисконта (процента).

Для упрощения анализа мы предполагаем, что после внедрения инновации меняется только уровень прибыльности производства, в то время как цена и объем выпускаемой продукции остаются неизменными. [2]

Общая идея формулы (1) состоит в том, что инновационный эффект представляет собой разницу между выигрышем на текущих издержках, выражающимся в увеличении прибыльности хозяйственных операций компании, и капитальными затратами. При этом как текущие, так и капитальные денежные потоки дисконтируются в соответствии со ставкой процента i. Соответственно суть моделируемого процесса состоит в том, рассматриваемая компания может работать в рамках старого способа производства, а может осуществить капиталовложения в некие инновации, которые позволят ей перейти к новому способу производства с большей величиной текущей отдачи (g_S<g_N).

Введенный показатель инновационного эффекта позволяет перейти к относительному показателю рентабельности реализуемой инновации r₀: .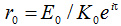

Если предположить, что все наши переменные являются константами, x₀, p₀, g_S0, и g_N0 – начальные значения соответствующих величин, а объем производства компании изменяется с постоянным темпом прироста λ=(1/x)(dx/dt), то с учетом введенного понятия эффективности (рентабельности) инноваций r₀ можно записать следующее условие инновационного равновесия:

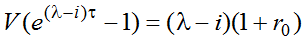                                                          (2)

где для компактности записи в левой части использован следующий коэффициент пропорциональности: .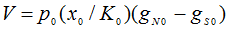

Соотношение (2) имеет элегантную интерпретацию с точки зрения теории экспектаций (ожиданий). Так, параметр эффективности инноваций r₀ может классифицироваться как предполагаемый (ожидаемый) процент прибыли, получаемый за период времени с каждого рубля, вложенного в инновацию.

Если на практике выполняется уравнение (2), то осуществление инновации является сомнительным. Если левая часть больше правой, то инновация считается оправданной; в противном случае инновация отвергается. Таким образом, вид знака в соотношении (2) задает своеобразную инновационную дихотомию.

Геометрия процесса влияния дисконта на инновационные решения предприятий

Теперь рассмотрим более предметно характер влияние дисконта на решения об осуществлении инноваций. Для этого воспользуемся уравнением (2), которое помимо всего прочего содержит три важных экономических параметра: темп роста производства (продаж), дисконт (ставку процента) и общую рентабельность инноваций. Особый интерес здесь представляет механизм переплетения двух виртуальных (ожидаемых) величин: дисконта (нормы процента) и рентабельности инноваций.

Прежде чем установить некое соответствие между ними, приведем их к сопоставимому виду. Дело в том, что величина r₀ является интегральной для рассматриваемого периода , в то время как для перехода к среднегодовой величине рентабельности инноваций r следует воспользоваться простыми соотношениями: .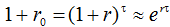

При оценке инвестиционных проектов показатель дисконта традиционно выступает в качестве ожидаемой нормы прибыли на вложенный инвестиционный рубль. Иными словами, дисконт – это тот уровень отдачи от инвестиций, который инвестор считает приемлемым для себя. Таким образом, инвестор, вкладывающий деньги в инновационные проекты, по сути дела отождествляет две величины: среднегодовую рентабельность инноваций и ставку дисконта, то есть r=i. К аналогичному результату можно прийти, отталкиваясь от того факта, что в качестве минимальной рентабельности инноваций выступает безрисковый дисконт, который можно получить при работе с соответствующими финансовыми инструментами. Это может быть процент по государственным облигациям или депозитный процент в высоконадежном банке. Эффективность инноваций ниже безрискового дисконта не стимулирует инвестора к вложениям в инновации.

Таким образом, приняв поведенческую гипотезу о равенстве среднегодовой рентабельности инноваций и ставки дисконта (i=r), уравнение (2) можно записать следующим образом:

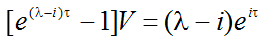                                                                   (3)

Выведенное уравнение (3) позволяет проанализировать инновационную дихотомию в контексте влияния на нее ставки дисконта. Если левая часть (3) больше правой, то осуществляется «запуск» инновации; в противном случае эффективность инноваций оказывается недостаточной и смены старого хозяйственного уклада не происходит. Здесь и далее мы ограничимся рассмотрением режима экономического роста (λ>0) как наиболее интересного и репрезентативного для инновационной сферы, однако при необходимости можно осуществить анализ и для случая режима экономической рецессии (λ<0).

В дальнейшем будет удобно использовать соотношение (3), введя соответствующие обозначения для его левой и правой частей: Ω(i)=Ψ(i). Тогда влияние дисконта на характер дихотомии хорошо иллюстрируется с помощью взаимного расположения кривых Ω(i) и Ψ(i). Так, кривая Ω(i) относительно дисконта представляет собой убывающую экспоненту (рис.1). Кривая Ψ(i) описывает некую параболическую зависимость относительно параметра ставки процента (i), ветви которой направлены вниз (рис.1). Если в точке i=0 выполняется неравенство Ω(i)<Ψ(i), то это означает, что инновационные программы блокируются и никакое увеличение дисконта не способно переломить инновационную депрессию. По мере роста процента две кривые постепенно сближаются вплоть до пересечения в точке i=λ. Если в точке i=0 выполняется неравенство Ω(i)>Ψ(i), то в такой беспроцентной (бездисконтной) экономике инновации достаточно выгодны. Однако в некоей точке i* две кривые пересекаются и за пределами этого значения дисконта инновации являются недостаточно рентабельными и теряют смысл.

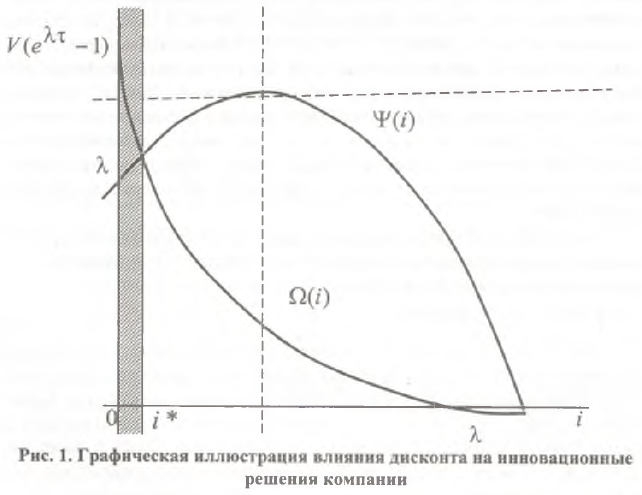
Определенного комментария заслуживает факт параболической формы кривой Ψ(i). Так, рассматриваемая функциональная зависимость представляет собой произведение прямой и экспоненты (рис.2). Их взаимное расположение в общем случае может быть различным: в случае взрывного роста (λ>1) они могут иметь точку пересечения как на рис.2; в случае более умеренного экономического роста они не пересекаются. Несложно убедиться, что итоговая кривая, являющаяся произведением прямой и экспоненты, имеет максимум в точке . Надо сказать, что вершина горба этой кривой может располагаться как в положительной, так и в отрицательной области оси абсцисс, однако это не меняет принципиального вывода об общей конфигурации параметров системы.

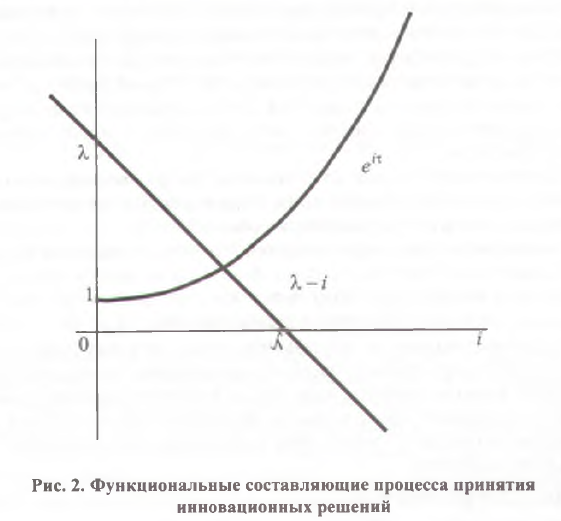
Уточненная геометрия процесса принятия инновационных решений позволяет пересмотреть сформулированную в предыдущей работе теорему о влиянии дисконта на инновации и дать ее в следующем виде:

Теорема: Принятие инвестором решения о внедрении инноваций происходит только при достаточно малых значениях дисконта, не превышающих величины темпа экономического роста компании: i<i*<λ.

Геометрическая интерпретация описанного процесса расслоения множества положительных значений дисконта на одну «эффективную» и одну «мертвую» полосы дана на рис.1 (эффективная полоса помечена штриховкой). Из теоремы о влиянии дисконта на инновации и взаимного расположения кривых на рис.1 вытекает важное следствие для режима i<λ: абсолютным пределом роста дисконта выступает темп экономического роста. При достижении критического состояния i=λ происходит полное «схлопывание» всех инновационных программ компании.

Содержательная начинка сформулированной теоремы также представляется очень простой. Фактически в ней речь идет о том, что при высоком дисконте начинает срабатывать эффект рантье, когда инвестору легче вложить имеющиеся в его распоряжении денежные средства в альтернативные финансовые инструменты (государственные облигации, банковский депозит), нежели осуществлять сомнительные инновации. Чтобы доход от инноваций подавил эффект рантье, государству необходимо поддерживать довольно низкие процентные ставки.

Инвариантность теоремы о влиянии дисконта на инновации относительно инвестиционных ожиданий

Выше мы сформулировали теорему о влиянии дисконта на инновации, исходя из того, что инвестор предполагает получить норму прибыли на вложенный капитал, равную дисконту. Однако, на первый взгляд, кажется, что подобная гипотеза является сильным ограничением степени общности анализа. Так, можно предположить, что инвестор по каким-либо причинам либо достаточно «жаден», либо достаточно «ленив». Тогда его ожидаемая норма прибыли, скорее всего, будет гораздо выше ставки дисконта. Такое возможно, в частности, когда в качестве инвестора и инноватора (менеджера предприятия) выступают разные физические лица. Если же собственник является одновременно еще инвестором и организатором производства, то для него инновации будут иметь стратегическое значение и он может удовлетвориться нормой прибыли, значительно меньшей, чем ставка дисконта. Таким образом, разные ожидания инвестора относительно дисконта могут приводить к разным инновационным стратегиям.

Логично задать вопрос: если инвестор сильно отклоняется в своих ожиданиях от ставки дисконта, то не будет и сам дисконт в этом случае по-другому влиять на инновационные решения?

Оказывается, отклонение ожиданий инвестора от дисконта не нарушает нарисованной картины процесса. В этом случае вместо гипотезы r=i принимается максимально общая схема: r=mi, где m – коэффициент согласования ожиданий инвестора и ставки дисконта. Если m=1, то инвестор идеально настроен на действующую ставку дисконта; если m>1, то норма дисконта его, вообще говоря, не удовлетворяет и он желает получить более весомую прибыль; если m<1, то инвестор сознательно отказывается от возможного более высокого дисконтного дохода в пользу планируемых инноваций. В этом случае соотношение (3) претерпевает минимальное изменение:

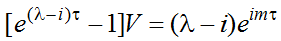                                                               (4)

Из записанного соотношения видно, что возможные вариации в ожиданиях инвесторов практически ничего не меняют в рассматриваемом процессе принятия инновационных решений. Геометрия процесса на рис.1 остается прежней, а введенный параметр m незначительно меняет лишь степень кривизны кривой Ψ(i) и немного смещает вдоль осей абсцисс и ординат точку максимума, достигаемую при ставке дисконта 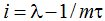. Возникающая таким образом незначительная деформация кривой Ψ(i) может лишь незначительно изменить значение критической точки i*, но не меняет общей направленности протекающих процессов. Таким образом, теорема о влиянии дисконта на инновации остается справедливой для любых инвестиционных ожиданий, а сам процесс принятия решений о внедрении рыночных нововведений инвариантен относительно степени «жадности» инвестора.

Возможно и еще одно важное обобщение полученных ранее выводов. Так, нами предполагалось, что инвестором осуществляется выбор между следующими альтернативами: продолжить работу предприятия по старой схеме или реорганизовать его работу за счет внедрения некоторой инновации. Однако все предложенные в статье конструкции могут быть использованы и для случая разрабатываемых новых инвестиционных проектов. Например, если принимается решение о запуске производства, которое будет давать чистый годовой доход в размере доли g₀ от объема продаж, то в этом случае формула (4) примет следующий вид:

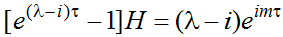                                                              (5)

где 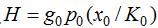 – коэффициент пропорциональности.

Таким образом, одна и та же схема анализа применима как к текущим инновациям, носящим характер неких хозяйственных усовершенствований, так и к стратегическим новшествам, стартующим с нулевого цикла. Роль дисконта в обоих случаях реализации инноваций одинакова.

Обобщенная теорема о влиянии дисконта на инвестиционные решения

Полученные аналитические зависимости позволяют выполнить важное обобщение относительно влияния дисконта как на инновационные, так и вообще на любые инвестиционные решения. Для этого достаточно рассмотреть два разных режима функционирования предприятия: i<λ и i>λ. Первый из указанных режимов фигурировал в теореме о влиянии дисконта на инновации, однако второй режим мы временно не рассматривали. Для этого достаточно рассмотреть соотношение (5) для двух соответствующих режимов. При этом в дальнейшем мы намеренно исключим из анализа фактор ожидаемой нормы прибыли на инвестируемый капитал, так как он по сути дела не меняет рисунка протекающих процессов (m=0).

Как и ранее ограничимся лишь геометрической интерпретацией всех построений для двух функциональных режимов, оставляя все обозначения прежними. Тогда графическая схема влияния дисконта на инвестиционные решения может быть представлена на рис.3, где штриховкой обозначена область дисконта, в которой происходит принятие инвестиционного проекта. Построенная геометрическая конструкция позволяет сформулировать обобщенную теорему о влияния дисконта на инвестиционные решения, которая учитывает оба функциональных режима экономического роста:

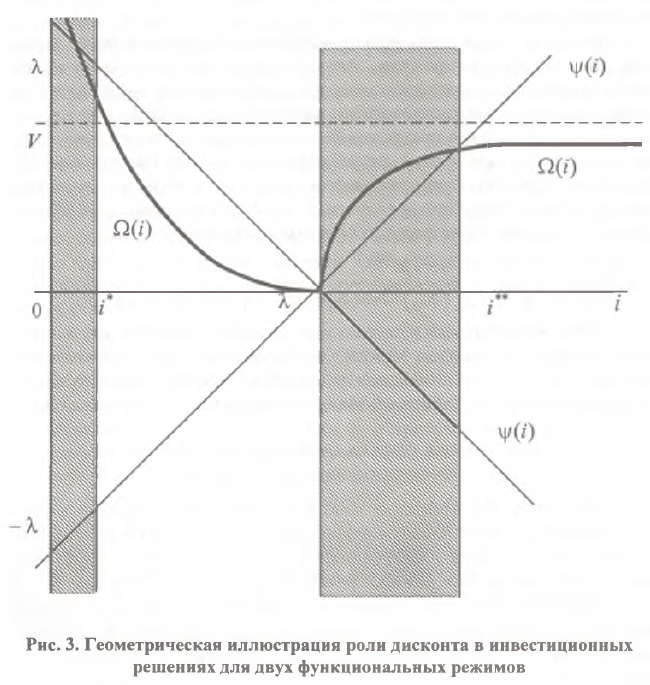
Теорема: При реализации режима интенсивного экономического роста, когда i<λ, принятие инвестором решения о внедрении проекта происходит только при достаточно малых значениях дисконта, не превышающих величину темпа экономического роста компании: i<i*<λ; при реализации режима вялого экономического роста, когда i>λ, положительное решение об инвестировании принимается только при значениях дисконта выше величины темпа экономического роста компании: i**>i>λ.

Таким образом, мы в очередной раз сталкиваемся со странной дихотомией в функционировании экономической системы. В зависимости от соотношения темпа роста производства (λ) и темпа капитализации (i) происходит коренной пересмотр инвестором своих инвестиционных и инновационных стратегий.

В данном случае мы имеем следующую динамическую картину влияния дисконта на преференции инвестора: при положительном темпе прироста выпускаемой продукции (λ>0) «хорошие» значения дисконта, при которых осуществляется запуск инвестиционного проекта, прижимаются справа к точке i=0. Если же некая критическая точка дисконта (i*<λ) превышена, то все инвестиционные проекты сворачиваются. Однако, как это ни парадоксально, оживить инвестиционную активность можно путем резкого повышения дисконта за пределы темпа экономического роста (i>λ). При этом «хорошие» значения дисконта снова прижимаются справа к точке отсчета, в качестве которой уже выступает i=λ. Если же дальнейшее повышение величины дисконта превысит критическую точку i** (i**>λ), то инвестиционная активность хозяйствующих субъектов снова подавляется.

Одна из интерпретаций сформулированной теоремы заключается в том, что для инновационных и быстро развивающихся рынков с ожидаемыми высокими темпами роста предпочтителен режим низких процентных ставок, в то время как для консервативных рынков со скромными перспективами расширения необходимо поддержание относительно высоких ставок дисконта. Другая интерпретация состоит в осознании разрыва в эффективных значениях дисконта: он оказывает стимулирующее действие либо когда его величина достаточно мала, либо достаточно велика. Какие-либо промежуточные значения дисконта оказываются неприемлемыми для инвестора. Хотя подобный «разрыв» дисконта возникает в ментальной сфере, а именно, в сознании инвестора, принимающего решение о запуске проекта, само его существование обусловлено специфической структурой капитализации и соизмерения во времени будущих доходов и издержек.

Обобщенная теорема о влиянии дисконта на инвестиционные решения вскрывает существование двух своеобразных «фокусов» на дисконтной шкале: i=0 и i=λ. Данные величины выступают в качестве неких точек притяжения эффективных значений ставки дисконтирования. Симптоматичным является тот факт, что указанные точки были «пойманы» и другими исследователями. Так, например, М.Алле еще в 1962 г. доказал теоремы, в соответствии с которыми оптимальный объем производства органически связан с двумя значениями дисконта: 0 и λ. [3] В частности, им было показано, что для статического случая, когда ключевые макроструктурные параметры постоянны, капиталистический производственный оптимум достигается при ставке процента i=0; для динамического процесса, когда структурные макропараметры изменяются, оптимальный выпуск достигается при ставке процента i=λ. Подчеркнем, что данный результат получен для экономики, не претерпевающей кардинальных изменений и не находящейся в переходном состоянии. М.Алле не рассматривал альтернативные пути развития хозяйственной системы и потому дисконт у него принимает точные «фокальные» значения. В нашей же постановке задачи моделируется дискретный процесс выбора самого пути развития и в этом случае вполне естественно, что эффективное значение дисконта имеет определенный допуск и «размазано» вокруг точек i=0 и i=λ. Любопытно, что эффективные значения дисконта лежат в некоей ε–окрестности двух «фокусов», которая в свою очередь всегда располагается справа от них.

Основной же смысл обобщенной теоремы о влиянии дисконта на инвестиционные решения заключается в установлении неочевидной взаимосвязи между такими важными экономическими параметрами, как темп роста производства и ставка дисконта.

Результаты экспериментальных расчетов

Хотя качественная характеристика функциональной дихотомии экономического роста дается обобщенной теоремой о влиянии дисконта на инвестиционные решения, для более полного уяснения действующих в данной сфере количественных закономерностей необходимо провести экспериментальные расчеты. В частности, можно «поиграть» величинами модельных параметров с целью нащупывания критических состояний системы. Наиболее интересным вопросом является определение критической величины дисконта i*, за пределами которой инвестиции вообще и инновации в частности становятся необоснованными.

Для уяснения степени чувствительности инновационной сферы к ставке дисконта нами выбран некий базовый вариант производственного проекта для режима λ>i (табл.1). Данный пример показывает, что знак в неравенстве (5) меняется при трудноуловимой величине дисконта, лежащей между величинами в 2,3 и 2,4% (эти элементы помечены темным цветом в табл.1). При дисконте выше 2,4% планируемые инновации становятся невыгодными.

Таблица 1. Взаимосвязь параметров процесса принятия инновационных решений (режим λ>i).

Полученная критическая ставка дисконта i*≈2,4% позволяет сделать вывод, что осмысленная процентная политика государства предполагает максимальное сдерживание эффективности финансовых операций. Приближение реальной ставки дисконта к 3% ставит под вопрос возможность проведения активной инновационной политики. Заметим, что данный вывод мы делаем применительно к нашему случаю, характеризующемуся чрезвычайно активной производственной программой в 30% ежегодного роста и далеко идущими хозяйственными планами, составляющими 4 года. Если эти показатели ухудшатся, то реализация инноваций станет еще более проблематичной. Важным является и то, что ширина «эффективной» полосы дисконта составляет в нашем случае менее одной десятой части от темпа экономического роста. Однако дополнительные численные эксперименты показывают, что при негативном изменении параметров абсолютная величина критической ставки дисконта уменьшается, а ее доля относительно темпа экономического роста возрастает. Так, уменьшение в нашем базовом сценарии темпа экономического роста в 10 раз (до 3% годовых) с одновременным увеличением горизонта планирования с 4 до 7 лет привело к тому, что переключение инновационного решения происходит при ставке дисконта между 1,4 и 1,5%. В этом случае абсолютная величина критической ставки дисконта уменьшилась примерно на 1 процентный пункт, а ширина «эффективной» дисконтной полосы увеличилась до 50% относительно темпа роста производства.

Таким образом, предполагаемый даже очень бурный рост компании с длительным горизонтом планирования может быть полностью нейтрализован депозитными ставками порядка 3% годовых. Данный аналитический результат говорит о том, что роль дисконта в принятии инновационных решений значительно выше, чем это принято считать. Учитывая данное обстоятельство, становятся понятными и некоторые моменты в международном развитии. Так, японские монетарные власти в течение многих лет поддерживали традиционно низкие процентные ставки. И именно Япония осуществила так называемое «экономическое чудо», на протяжении нескольких десятилетий внедряя разнообразные инновации.

Аналогичные расчеты для режима λ<i с параметром m=0 приведены в табл.2 и показывают, что критическая ставка дисконта составляет i**≈36,5% (граница переключения в табл.2 помечена темным цветом). Данный результат представляет особый интерес, прежде всего, потому, что позволяет сравнить ширину ε–окрестности двух «фокальных» значений дисконта: i=0 и i=λ. В первом случае эффективная полоса составляет ε=i*=2,4%, а во втором – ε=i**–λ=36,5–30=6,5%.

Таблица 2. Взаимосвязь параметров процесса принятия инновационных решений (режим λ<i).

Таким образом, режим высоких дисконтных ставок предполагает большую свободу маневра финансовых институтов, нежели режим низких процентных ставок. С этой точки зрения первый режим может считаться даже более предпочтительным. Однако не следует игнорировать тот факт, что не каждый инвестиционный и инновационный проект имеют такие параметры, при которых существуют две эффективные полосы. Данный факт служит серьезным ограничением практического применения обобщенной теоремы о влиянии дисконта на инвестиционные решения. По-видимому, не будет ошибкой утверждение, что указанная теорема в полной мере проявляется только для высокоэффективных проектов, способных окупиться как при низких, так и при высоких ставках дисконта.