В настоящее время российская экономика находится в состоянии инвестиционного кризиса, глубина которого является поистине рекордной. Иллюстрируя сказанное достаточно указать, что к 1997 г. в России доля капиталовложений в ВНП упала до 8,7%, в то время как аналогичный показатель в 1992 г. в США составлял 18,9%, Франции – 21,5, Японии – 32,9, Корее – 36,0, Сингапуре – 41,3 [1, С.13]. В соответствии с расчетами А.А.Водянова, для вывода страны на траекторию устойчивого экономического роста со среднегодовым темпом в 5% нынешняя норма накопления должна возрасти в 1,5–1,8 раза и достигнуть соответственно 13,0–15,6% [1, С.13]. По его мнению, достичь этого в обозримой перспективе не удастся, в том числе с помощью иностранных инвесторов. Следовательно, Россия стоит на пороге продолжительного периода нулевого экономического роста.

Хотя большинство аналитиков совершенно справедливо сходится во мнении, что иностранные инвестиции не в состоянии переломить затянувшуюся производственную рецессию, следует все же отметить, что, не имея собственных финансовых ресурсов, Россия в сложившейся ситуации просто вынуждена прибегать к помощи извне. Именно это российское правительство и делает, беря все новые и новые международные кредиты. Однако, как показывает опыт, такая политика обречена на неудачу. И не только из-за необходимости выплачивать проценты по долговым обязательствам, но и из-за отсутствия эффективных механизмов вовлечения полученных финансовых инъекций в реальный сектор экономики. В большинстве случаев полученные займы либо чрезвычайно нерационально используются, либо просто расхищаются. В возникшей тупиковой ситуации практически единственной надеждой остаются прямые иностранные инвестиции (ПИИ), которые представляют собой реально работающие финансовые вложения в российскую экономику.

Сказанное позволяет сформулировать ряд животрепещущих вопросов. Например, насколько оправданы пессимистические прогнозы в отношении будущего России? Можно ли, активизировав приток ПИИ, в сжатые сроки поднять уровень общей инвестиционной активности в стране и тем самым заложить основу будущего экономического роста? Сложились ли в России условия для эффективного использования ПИИ?

Ответы на поставленные вопросы предполагают, во-первых, решение задачи прогнозирования экономического развития России, а, во-вторых, выработку принципиальной позиции в отношении ПИИ. И то, и другое возможно только на основе достоверных экономических расчетов, которые должны базироваться на установленных количественных связях между соответствующими макроэкономическими переменными. Однако именно это пока чрезвычайно трудно сделать в силу отсутствия необходимого массива информации.

Данный факт предопределяет решение поставленной задачи “обходным” путем, то есть опираясь на международные закономерности влияния иностранного капитала на инвестиционную активность стран–реципиентов. Между тем широкий спектр имеющихся научных работ по данной теме не в состоянии дать удовлетворительные ответы на поставленные вопросы. Так, например, для многих развивающихся стран уже проведены детальные эконометрические исследования, которые либо подтверждают, либо отрицают позитивную роль ПИИ. Тем не менее масса вопросов до сих пор так и не получила удовлетворительных ответов.

Целью данной статьи является критическое рассмотрение некоторых типичных подходов к анализу роли ПИИ для принимающей страны, а также разработка схемы такого анализа применительно к экономике переходного периода. Предлагаемая схема предполагает две разновидности: для случая, когда не хватает исходной информации, и, когда вся необходимая информация имеется.

ОБЩИЕ ПРОБЛЕМЫ ИССЛЕДОВАНИЯ ЗАКОНОМЕРНОСТЕЙ МЕЖСТРАНОВОГО ДВИЖЕНИЯ ПИИ

Независимо от технических особенностей проводимых исследований в области ПИИ, все они недостаточно удовлетворительны с прогнозной точки зрения. Можно выделить следующие основные группы проблем.

1. Все проводимые эконометрические исследования носят, как правило, специфический характер, охватывая либо одну отрасль экономики, либо одну страну. Соответственно остаются за бортом общие тенденции “жизни” прямых иностранных инвестиций. Между тем чрезвычайно важно кластировать все страны на группы, в которых наблюдаются разные закономерности. Большое значение в этом случае приобретают масштаб рассматриваемой экономики, средний уровень инвестиционной активности в ней, средние объемы привлекаемых ПИИ и т.д. Дифференциация стран в зависимости от значений названных показателей позволила бы правильней понять истинное значение международного движения капиталов. Отсутствует пока и четкое представление о величинах точек “перелома”, за пределами которых ПИИ начинают оказывать то или иное воздействие. Сюда же примыкает вопрос об асимптотике процесса.

2. До сих пор остается открытым вопрос о временных лагах между внутренней инвестиционной активностью страны–реципиента и деятельностью ПИИ. Причем помимо наличия или отсутствия самих запаздываний принципиальное значение имеет вопрос о “ведущем” факторе, то есть какой из феноменов является первичным и, следовательно, что за чем следует: ПИИ за внутренней инвестиционной активностью или наоборот?

3. В работах, посвященных эконометрическому анализу роли ПИИ, как правило, даже не поднимается вопрос о значении фактора стабильности их поступления в экономику принимающей страны. Между тем очевидно, что при больших объемах ПИИ сбои в ритмичности их поступления должны существенно влиять на общий инвестиционный климат в стране. Аналогичная гипотеза использовалась О.О.Замковым при исследовании связи между уровнем инвестиционной активности и темпами инфляции [2, С.72]. Применительно к связи между внешними и внутренними инвестициями подобная гипотеза, насколько нам известно, не проверялась.

4. Все вопросы о связи внутренней инвестиционной активности и ПИИ в постсоциалистических странах остаются открытыми и будут оставаться таковыми еще долгое время (по нашим оценкам около 5 лет). Это связано с тем, что процесс привлечения ПИИ в этих странах имеет слишком короткую историю. Так, например, в России это период с 1990 г. Понятно, что достоверные эконометрические расчеты по столь коротким временным рядам невозможны. В этой связи особое значение приобретает межстрановой анализ и выявление групп стран с одинаковыми функциональными свойствами, так как впоследствии это позволит разнести постсоциалистические страны по соответствующим кластерам и на этой основе предсказывать для них возможный эффект от ПИИ. Иного способа эффективного прогнозирования развития событий в странах с “молодой” рыночной экономикой, на наш взгляд, практически не существует.

ЭКОНОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ ПИИ (КРИТИЧЕСКИЙ АНАЛИЗ СУЩЕСТВУЮЩИХ ПОДХОДОВ)

Все современные эконометрические исследования ПИИ условно можно разделить на два больших класса. Первый предполагает моделирование влияния различных факторов на объемы ПИИ, то есть иностранные инвестиции фигурируют в качестве “выходной” переменной принимающей экономики, а задача исследования заключается в выборе соответствующей факторообразующей зависимости и самого набора факторов. Второй класс исследований ориентирован на решение “обратной” задачи, а именно: проследить влияние ПИИ на основные макроэкономические характеристики. Следовательно, здесь ПИИ выступают в качестве “входной” переменной (фактора).

Рассмотрим более подробно некоторые, наиболее важные подходы к анализу ПИИ. При этом сразу оговоримся, что в данной работе мы намеренно не будем обсуждать те количественные результаты, которые получены в сфере ПИИ различными исследователями с помощью эконометрических моделей; здесь нас будет интересовать только методическая сторона применяемого ими инструментария.

К первому классу моделей относится, в частности, эконометрическая зависимость, использованная К.Мильнером (С.Milner) и Е.Пинтекостом (Е.Pentecost) при исследовании потоков американских прямых инвестиций в отрасли английской экономики [3, С.93]:

                                              (1)

где F – объем прямых инвестиций США в отрасль Великобритании; x₁ – индекс открытого относительного преимущества или торговое наполнение отраслевого продукта; x₂ – ежегодный процентный рост протекции отраслевого продукта; x₃ – уровень конкурентоспособности отраслевого продукта; x₄ – размер рынка отраслевого продукта (объем производства или продаж); α₀, α₁, α₂, α₃ и α₄ – оцениваемые параметры.

Помимо этого, К.Мильнером и Е.Пинтекостом были предложены алгоритмы для расчета отраслевых индикаторов x₁, x₂, x₃ и x₄. Для оценки параметров α₀, α₁, α₂, α₃ и α₄ использовался массив из 48 отраслей за 1990 г. Таким образом, для получения необходимой для расчетов выборки авторы проводили эконометрический анализ в отраслевом разрезе и, следовательно, коэффициенты регрессии (1) получались одинаковыми для всех британских отраслей.

Несмотря на “обычность” модели Мильнера–Пинтекоста, она все же имеет ряд недостатков, среди которых укажем следующие.

1. Оценка значений аргументов-факторов в уравнении (1) неоднозначна, так как предполагает использование альтернативных показателей, некоторые из которых выглядят довольно искусственно. Иными словами, вычисление факторов–индикаторов представляет собой самостоятельную проблему и использование отраслевых рядов, состоящих из подобных “вторичных” статистических конструкций, вряд ли может считаться безупречным с точки зрения регрессионного анализа; для обеспечения “чистоты” выявленных корреляционных связей желательно использовать максимально простые статистические показатели с абсолютно прозрачным экономическим смыслом.

2. Учитывая, что техническая процедура отыскания коэффициентов регрессии авторами [3] переводится в “отраслевую” плоскость, эти коэффициенты, во-первых, одинаковы для всех отраслей, а, во-вторых, различны для всех анализируемых лет. Однако подобные постулаты нуждаются в дополнительном обосновании и не могут быть приняты как нечто само собой разумеющееся.

3. Процедура построения удовлетворительной регрессионной зависимости и выяснения значимости в ней каждого фактора представляет собой своеобразную подгонку альтернативных показателей–факторов под исходную линейную функцию (1) с последующим отбрасыванием их неудачных сочетаний [3, С.97,100]. Таким образом, выбор окончательной модели не имеет серьезного теоретического обоснования, целиком базируясь на вычислительных экспериментах.

Аналогичный, но более простой с методологической точки зрения, подход к определению факторов привлечения ПИИ был развит В.Н.Баласубраманьямом (V.N.Balasubramanyam) и Д.Гринэвэем (D.Greenaway) при рассмотрении японских прямых инвестиций в страны еврорынка [4, С.119]. Базовая модель в их случае совпадает с зависимостью (1):

                                                            (2)

где F – объем японских прямых инвестиций в страны еврорынка, а содержательное наполнение аргументов–факторов в (2) сильно отличается от того, который предполагала модель (1), а именно: x₁ – совокупный валовой внутренний продукт (ВВП) стран еврорынка; x₂ – темп роста совокупного ВВП стран еврорынка; x₃ – отношение японского экспорта к совокупному объему экспорта между странами еврорынка; α₀, α₁, α₂, и α₃ – оцениваемые параметры.

При проведении вычислительных экспериментов В.Н.Баласубраманьям и Д.Гринэвэй использовали различные модификации модели (2), либо добавляя в базовую регрессию дополнительный фактор α₄x₄(t), где x₄ – доля совокупных продаж стран еврорынка между собой в их общем объеме продаж, либо преобразуя исходную линейную зависимость (2) к логарифмически–линейному виду [4, С.120]:

                                        (3)

Метод Баласубраманьяма–Гринэвэя имеет примерно те же недостатки, что и модель Мильнера–Пинтекоста. Основные из них следующие.

1. Авторы [4] довольно произвольно экспериментируют как с набором факторов регрессионной функции, так и с ее конкретным видом. Последний момент представляется особенно “скользким”, ибо переход от зависимости (2) к (3) фактически означает переход от линейного к нелинейному виду связи, что методически несопоставимо.

2. Из рассмотренных в [4] четырех экономических зависимостей в конечном счете оказывается невозможно выбрать одну, наиболее удачную модель. Это сильно уменьшает прикладное значение полученных результатов и позволяет делать лишь качественные выводы о значимости каждого фактора.

3. В.Н.Баласубраманьям и Д.Гринэвэй используют “временной” срез эконометрического анализа, что предполагает постоянство во времени коэффициентов регрессии и тем самым противоречит, например, “отраслевой” идеологии Мильнера–Пинтекоста.

Ко второму классу моделей относятся, в частности, модели, предложенные Максвеллом Дж.Фраем (M.J.Fry) в работе [5], посвященной анализу инвестиционных связей в экономике Малайзии. М.Дж.Фрай использует два подхода для выяснения роли ПИИ. Первый основывается на двухшаговой эконометрической процедуре и предполагает независимую оценку двух зависимостей [5, С.191–193]:

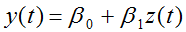                                                                                                 (4)

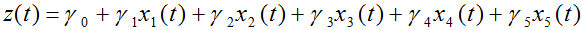                                   (5)

где y – доля внутренних инвестиций в объеме ВНП (для экономики Малайзии); z – доля сбережений в ВНП; x₁ – темп роста национального продукта; x₂ – отношение численности населения в возрасте до 15 лет и после 64 лет к численности населения в возрасте от 15 до 64 лет; x₃ – натуральный логарифм индекса концентрации доходов Джини; x₄ – доля инвестиций общественного сектора в ВВП; x₅ – доля прямых иностранных инвестиций (в экономику Малайзии) в ВНП; β₀, β₁, γ₀, γ₁, γ₂, γ₃, γ₄ и γ₅ – оцениваемые параметры.

Из зависимостей (4) и (5) легко получить соотношение между внутренней и внешней инвестиционной активностью, то есть

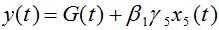                                                                                          (6)

Переменная G в (6) аккумулирует все прочие факторы влияния на активность внутренних инвестиций, кроме фактора ПИИ.

Второй подход предполагает одношаговую процедуру построения инвестиционной функции

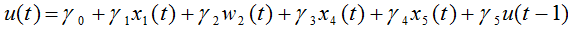                               (7)

где u – доля совокупных инвестиций в ВНП (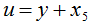); w₂ – натуральный логарифм торгового индекса; остальные переменные несут ту же смысловую нагрузку, что и аналогичные показатели в уравнении (5); γ₀, γ₁, γ₂, γ₃, γ₄ и γ₅ – оцениваемые параметры.

Метод М.Дж.Фрая также имеет недостатки, среди которых наиболее важными представляются следующие.

1. При сопоставлении двух подходов, развитых М.Дж.Фраем, обращает на себя внимание тот факт, что они логически противоречивы. Так, например, в уравнениях (4)–(5) присутствует фактор структуры распределения доходов населения (индекс Джини), а в уравнении (7) отсутствует даже какой-либо его аналог. Вместе с тем в (7) учитывается автокорреляционный эффект, в то время как в (4)–(5) его нет. Сказанное свидетельствует о том, что на базе разных исходных гипотез и методологических подходов могут получаться эконометрические результаты, сопоставимые по уровню статистической надежности.

2. Предлагая два альтернативных подхода М.Дж.Фрай не предлагает никаких критериев и алгоритмов предпочтения одного другому. Таким образом, выбор между “одношаговым” и “двухшаговым” методами на практике осуществляется в значительной мере произвольно.

В другой, более ранней работе [6], посвященной взаимосвязи между инвестиционной активностью и движением международного капитала, Мартин Фельдстейн (M.Feldstein) и Чарльз Хориока (C.Horioka) используют базовую модель (4) с той лишь разницей, что в их случае фигурируют доли отечественных инвестиций и сбережений в ВВП, а не в ВНП, как в случае М.Фрая.

Помимо этого, М.Фельдстейн и Ч.Хориока используют модификацию уравнения (4), учитывающую степень открытости экономики страны [6, С.322]

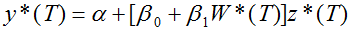                                                                           (8)

где y* – средняя доля отечественных (внутренних) инвестиций в ВВП за анализируемый период времени T=1960–1974; z* – средняя доля сбережений в ВВП за этот же период времени; W* – средний показатель “открытости” или, наоборот, “закрытости”, экономики, рассчитываемый как отношение внешнеторгового оборота (суммы экспорта и импорта) к ВВП; α, β₀ и β₁ – параметры.

Технически эконометрическая оценка параметров модели (4) М.Фельдстейном и Ч.Хориокой переводится в “региональную” плоскость, то есть ими используется массив средних за период времени 1960–1974 гг. величин для 16 стран ОЭРС [6, С.319]. Соответственно, получаемые коэффициенты регрессии одинаковы для всех изучаемых государств.

Дальнейший шаг в анализе инвестиционных эффектов связан с построением регрессионной зависимости для z₁(T), которая во многом похожа на зависимость (5), используемую М.Фраем; z(T)=z₁(T)+z₂(T), где z₁(T) – доля частных сбережений в ВВП; z₂(T) – доля государственных сбережений в ВВП [6, С.324].

Помимо простейшей агрегированной зависимости (4) М.Фельдстейн и Ч.Хориока в дальнейших исследованиях используют также ее дезагрегированную форму

                                                                  (9)

где z₁(T), z₂(T) и z₃(T) – сбережения домашних хозяйств, корпораций и государства, соответственно.

Несложно видеть, что модели М.Фельдстейна и Ч.Хориоки также не лишены целого ряда очевидных недостатков.

1. В уравнение (8) весьма догматически введен фактор открытости экономики. Не дается М.Фельдстейном и Ч.Хориокой никаких обоснований и мультипликативной связи коэффициента W(T) и доли z(T). В этой связи не удивительно, что эконометрические расчеты дали отрицательную оценку β₁, хотя в соответствии с теоретическими рассуждениями она должна была бы быть положительной [6, С.322]. На наш взгляд, фактор открытости уже “сидит” в зависимости (4), когда в ней вместо ВВП используется показатель ВНП.

2. По сути дела М.Фельдстейн и Ч.Хориока не провели в явной форме анализа ПИИ на внутреннюю инвестиционную активность стран ОЭСР. Данный аспект учитывается ими косвенно, путем изменения интерпретации самой зависимости (4). Так, если доля отечественных инвестиций превышает долю внутренних сбережений, то это означает приток в страну иностранных инвестиций. Регрессия (4) в этом случае модифицируется таким образом, что в левой части стоит доля иностранных инвестиций в ВВП, а в правой части вместо коэффициента β₁ следует брать коэффициент (β₁–1). Если при эконометрической оценке β=1, то это означает, что иностранные инвестиции не зависят от внутренней нормы сбережений и, соответственно, сами не влияют на ее уровень. На наш взгляд, для выяснения подобных эффектов следует все–таки строить дополнительную эконометрическую зависимость и тем самым переходить к “двухшаговой” процедуре, которую впоследствии использовал М.Фрай.

3. Остается под сомнением прогностическая способность подхода Фельдстейн–Хориоки, так как полученные ими оценки применимы к данным, усредненным за длительный период времени; на определенных, не очень длинных, временных интервалах возможны сильные отклонения от установленной зависимости.

Перечисленные эконометрические методы исследования ПИИ помимо сугубо частных имеют и общие недостатки. К их числу относятся следующие.

1. При построении конкретного вида эконометрической зависимости подавляющее большинство исследователей не располагает стройной теорией, которая, собственно говоря, и должна была бы подвергаться статистической проверке.

2. Для предлагаемых моделей характерна методическая эклектичность (например, равноправное существование “одношагового” и “двухшагового” методов М.Дж.Фрая, проведение эконометрической оценки параметров в “отраслевой”, “региональной” и “временной” плоскости и т.д.).

3. Бессистемное, хаотичное “нащупывание” эконометриками набора определяющих факторов эконометрической зависимости и ее конкретного вида.

МЕТОДОЛОГИЯ АНАЛИЗА И ПРОГНОЗИРОВАНИЯ ЭФФЕКТА ОТ ПИИ В УСЛОВИЯХ НЕХВАТКИ ИНФОРМАЦИИ

На стадии, когда еще не накопился массив отчетной информации о динамике ПИИ в переходной экономике, для прогнозирования эффекта от их активизации можно воспользоваться ниже предполагаемой процедурой.

Весь алгоритм прогнозирования антикризисного эффекта ПИИ применительно к экономике России может быть разбит на три этапа.

I. Сопоставление основных экономических характеристик российской экономики и экономик других стран мира и формирование на этой основе кластера стран с макропоказателями, сходными с российскими. Полученный кластер в дальнейшем будем называть “базовым”. В качестве сравнительных показателей следует использовать: долю ПИИ в ВНП (или ВВП); долю отечественных капиталообразующих инвестиций в ВНП; показатели масштаба экономики (численность населения, объем ВНП, размер территории и т.д.).

II. Установление зависимости между долями внутренних капиталовложений и ПИИ в ВНП для стран из “базового” кластера стран. Искомое регрессионное уравнение предлагается брать линейным с учетом следующих трех аспектов.

1. Так как большинство исследований инвестиционной активности выявляют устойчивый авторегрессионный эффект [2;5], то и в нашей зависимости следует предусматривать авторегрессионный член. Данный подход отражает тот факт, что инвестиционный процесс всегда обладает определенной инерционностью, то есть инвестиции в уже начатые проекты продолжают осуществляться даже если внешние условия изменились. Как правило, длительность временного лага не превышает одного года, в связи с чем именно эту гипотезу и следует использоваться в конкретных расчетах.

2. Учитывая, что в развитии любого реального процесса существуют точки бифуркации, в которых меняется характер функциональной зависимости, в искомом регрессионном уравнении мы предусматриваем наличие границы, за которой ПИИ не воздействуют на внутреннюю инвестиционную активность. Оценка параметров регрессии такого рода позволяет эконометрически определить зону “нечувствительности” экономики к воздействию ПИИ. Аналогичный подход использовался в [2, С.77–78].

3. Исходя их общих соображений, правомерно предположить, что ПИИ активизируют внутреннюю инвестиционную деятельность не сразу, а спустя лишь некоторое время. Следовательно, в уравнении регрессии фактор ПИИ должен фигурировать с лагом, величина которого должна определяться в результате эконометрических экспериментов.

Таким образом, регрессионное уравнение, подлежащее статистической проверке, имеет вид:

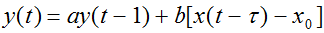                                                                      (10)

где y – доля внутренних (отечественных) инвестиций в ВНП; x – доля ПИИ в ВНП; t – время (год); 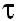– временной лаг; α, b и x₀ – параметры.

III. Расчет экономического эффекта от ПИИ. Это достигается элементарно при наличии зависимости (10) и балансового уравнения 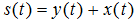, где s – доля совокупных инвестиций в ВНП. Расчет следует вести в обратную сторону: зная долю s*, необходимую для вывода российской экономики из кризиса, можно пересчитать необходимый прирост ПИИ x* и оценить получившуюся величину на реалистичность. Ниже мы более подробно остановимся на анализе связи ПИИ и экономического роста страны-реципиента.

Если рассматривается переходная экономика, для которой собрана вся необходимая для расчетов информация, то этап №I вышеприведенной схемы становится излишним и его можно пропустить. В этом случае этап №II становится особенно актуальным и интересным.

АКТИВИЗАЦИЯ ПИИ И ЭКОНОМИЧЕСКИЙ РОСТ: МЕТОДИКА АНАЛИЗА

Отдельного рассмотрения заслуживает вопрос о том, как влияет активизация ПИИ на динамику экономического роста страны–реципиента. Особенность данной проблемы заключается в том, что для ее строгого решения необходимо осуществить методический синтез традиционных моделей экономического роста и эконометрических моделей, выявляющих связь между внутренней и внешней инвестиционной активностью. Для переходных экономик подобное возможно только на следующем этапе развития, когда накапливаются достаточно длинные ретроспективные динамические ряды.

Для “слияния” двух типов моделей можно, в частности, воспользоваться следующим соотношением, полученным в [7]:

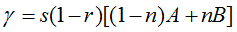                                                                                        (11)

где γ – темп прироста ВВП; r – доля промежуточного потребления в валовом продукте. Общий объем инвестиций в (11) складываются из двух агрегатов: 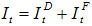, где 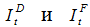 – инвестиции, осуществляемые отечественными предприятиями и предприятиями с участием иностранного капитала, соответственно. Показатели A и B – капиталоемкость отечественного и зарубежного секторов соответственно;  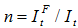– доля инвестиций зарубежного сектора в общем объеме капиталовложений (более подробно об (11) см. [7]).

Введем в рассмотрение дополнительные параметры: 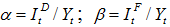, где Y_t – объем валового внутреннего продукта.

Формула (11) фиксирует зависимость темпов экономического роста (γ) от общей инвестиционной активности в стране (s), доли инвестиций иностранного сектора (n) и отдачи от инвестиций в двух секторах (A и B).

Однако применительно к нашей постановке задачи формула (11) не может использоваться напрямую, так как нам необходимо выяснить не то, как влияет на экономический рост изменение структуры инвестиций (то есть изменение параметра n), а увеличение активности ПИИ (то есть рост параметра β). Учитывая, что 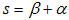, уравнение (11) можно переписать в виде:

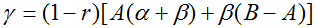                                                                                (12)

Если все параметры (12) оценены и установлена эконометрическая зависимость между внутренней и внешней инвестиционной активностью в виде регрессии общего вида

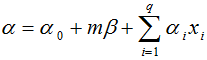                                                                                            (13)

то из (12) и (13) автоматически вытекает соотношение

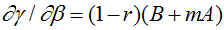                                                                                          (14)

Из (14) следует, что рост активности ПИИ стимулирует экономический рост в принимающей стране, если выполнено условие:

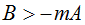(15)

Если для рассматриваемой страны статистических данных недостаточно для оценки параметра m, то можно взять его величину для страны, наиболее близкой к изучаемой (то есть из соответствующего кластера). Такой подход может использоваться для “черновых” прогнозов экономического развития переходной экономики.

Проиллюстрируем работу неравенства (15).

В 1994–1995 гг. для экономики России были характерны следующие величины акселераторов: A=–0,55; B=2,26 (см. [7]). Если предположить, что значение параметра m=0,617 (именно такая величина была эконометрически установлена для экономики Малайзии в [5]), то условие (15) выполняется:

2,26 > 0,55 x 0,617 = 0,34.

Таким образом, в 1994–1995 гг. в России были созданы условия, когда рост активности ПИИ был бы чрезвычайно полезен для экономики, содействуя росту национального производства.

Иная ситуация была характерна для 1995–1996 гг., когда экономика России обладала следующими параметрами: A=–0,65; B=0,35. При m=0,617 условие (15) не выполняется:

0,35 < 0,65 x 0,617 = 0,40.

Следовательно, в 1995–1996 гг. ситуация в России кардинально изменилась и повышение инвестиционной активности за счет ПИИ было нецелесообразным, так как это только бы подрывало экономический рост.

Если рассматривается переходная экономика имеет достаточный срок “жизни” и для нее накоплены все необходимые эмпирические данные, то в качестве параметра m берется его “родное” значение, полученное на базе эконометрических расчетов.

* * *

В данной работе нами были предложены подходы, направленные на выяснение роли ПИИ для формирования внутреннего инвестиционного климата в принимающей стране и, соответственно, для стимулирования экономического роста. Безусловно, все они являются “сырыми”, так как еще не апробированы на конкретных данных. Однако, нам представляется, что это необходимый этап для успешного проведения дальнейших, более плодотворных исследований в данной области.

ЛИТЕРАТУРА

[1] Водянов А.А. Лабиринт стагнации (“Эксперт”, №3(120), 26 января 1998).

[2] Замков О.О. Инфляция и инвестиции в рыночной экономике (“Вестник Московского университета. Серия 6, Экономика”, №3, 1995).

[3] Milner C., Pentecost E. The determinants of the composition of US foreign direct investment in UK manufacturing (“The Economics of International Investment”/ Edited by V.N.Balasubramanyam, D.Sapsford. Cornwall, 1994).

[4] Balasubramanyam V.N., Greenaway D. East Asian foreign direct investment in the EC (“The Economics of International Investment”/ Edited by V.N.Balasubramanyam, D.Sapsford. Cornwall, 1994).

[5] Fry M.J. Malaysia’s inverse saving–investment correlation: the role of public and foreign direct investment (“The Economics of International Investment”/ Edited by V.N.Balasubramanyam, D.Sapsford. Cornwall, 1994).

[6] Feldstein M., Horioka C. Domestic saving and international capital flows (“The Economic Journal”, Vol.90, No.358 (June). 1980).

[7] Балацкий Е.В. Иностранный бизнес и его влияние на экономику страны–реципиента (“Мировая экономика и международные отношения”, №*, 1999).

Официальная ссылка на статью:

Балацкий Е.В. Прямые иностранные инвестиции и внутренняя инвестиционная активность// «Мировая экономика и международные отношения», №11, 1999. С.83–89.