Происходящий в настоящее время переход к системе рыночных отношений сопряжен прежде всего с ускоренным проведением крупномасштабных структурных сдвигов в экономике. Такое положение определяет особую актуальность и значимость вопросов, связанных с анализом и прогнозированием направлений, скорости и эффективности структурных изменений, ибо корректный ответ на данные вопросы служит основой для разработки прогрессивной структурной политики. Однако проведенный анализ показал, что при оценке скорости и эффективности структурных сдвигов в экономике возникает целый ряд информационно–методических проблем, рассмотрению которых и посвящена данная статья.
Для определения эффективности структурных изменений будем использовать традиционный подход, позволяющий оценить степень влияния происходящих сдвигов на динамику таких сводных показателей эффективности, как народнохозяйственная фондоотдача (фондоемкость), капиталоотдача (капиталоемкость), металлоемкость, энергоемкость, материалоемкость, производительность общественного труда и т.п.
При оценке эффективности структурных сдвигов используются структурные тождества, которые, как правило, имеют следующий вид: 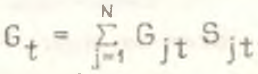 Пусть для определенности введенные обозначения имеют следующий содержательный смысл: t – индекс времени; j – индекс отрасли, j=1̅,̅N̅; Gt – производительность общественного труда; GJt – производительность труда в отрасли j; Sjt – доля занятых в отрасли j в общей численности занятых по народному хозяйству (экономическая интерпретация используемых переменных может быть различной в зависимости от анализируемого показателя эффективности, так как указанное тождество представляет собой достаточно общий случай структурной зависимости). Тогда при дифференцировании по времени данное тождество примет следующий вид:
Пусть для определенности введенные обозначения имеют следующий содержательный смысл: t – индекс времени; j – индекс отрасли, j=1̅,̅N̅; Gt – производительность общественного труда; GJt – производительность труда в отрасли j; Sjt – доля занятых в отрасли j в общей численности занятых по народному хозяйству (экономическая интерпретация используемых переменных может быть различной в зависимости от анализируемого показателя эффективности, так как указанное тождество представляет собой достаточно общий случай структурной зависимости). Тогда при дифференцировании по времени данное тождество примет следующий вид:
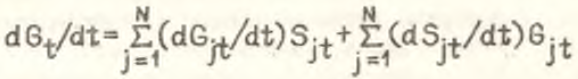 (1)
(1)
Второе слагаемое правой части разложения (1) представляет собой оценку структурного эффекта (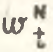 ), которая характеризует эффективность происходящих структурных сдвигов. Однако данная оценка справедлива лишь для рассматриваемого уровня отраслевого агрегирования. В случае дезагрегирования исходной N–отраслевой структуры до уровня N̅–отраслевой (N̅>N) величина структурного эффекта (
), которая характеризует эффективность происходящих структурных сдвигов. Однако данная оценка справедлива лишь для рассматриваемого уровня отраслевого агрегирования. В случае дезагрегирования исходной N–отраслевой структуры до уровня N̅–отраслевой (N̅>N) величина структурного эффекта (.png) ) может не совпадать с оценкой
) может не совпадать с оценкой  , т.е. возникает смещение оценок, что позволяет говорить о проблеме инвариантности (устойчивости) структурного эффекта относительно преобразования уровня агрегирования.
, т.е. возникает смещение оценок, что позволяет говорить о проблеме инвариантности (устойчивости) структурного эффекта относительно преобразования уровня агрегирования.
Рассмотрим частный случай, который хорошо иллюстрирует возникновение смещения оценок структурных эффектов при переходе на новый уровень отраслевого агрегирования.
Пусть имеется стационарная структура из N отраслей, т.е. структурные сдвиги отсутствуют: dSjt/dt=0, j=1̅,̅N̅ . Тогда структурный эффект (.png) ) представляет собой второй компонент правой части разложения (1)
) представляет собой второй компонент правой части разложения (1) .png) = 0.
= 0.
Рассмотрим теперь ту же структуру, где отрасль N разбивается на две подотрасли: N1 и N2. При этом имеется структурный сдвиг между этими подотраслями, в то время как их суммарный удельный вес не изменяется: 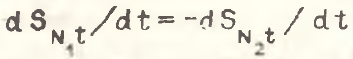 . Тогда структурный эффект для данного уровня агрегирования (N+1) равен
. Тогда структурный эффект для данного уровня агрегирования (N+1) равен
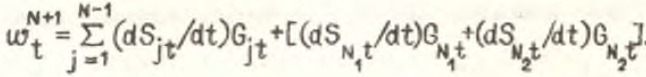 (2)
(2)
Первый компонент правой части формулы (2) равен нулю, а выражение в квадратных скобках равно нулю в случае 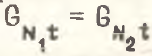 . Если же средние производительности труда в подотраслях не совпадают (что, как правило, имеет место в реальной экономике), то
. Если же средние производительности труда в подотраслях не совпадают (что, как правило, имеет место в реальной экономике), то 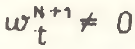 и, следовательно,
и, следовательно, 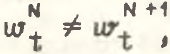 т.е. происходит смещение оценок структурного эффекта (очевидно, что внутриотраслевые эффекты при этом также не равны для разных уровней агрегирования).
т.е. происходит смещение оценок структурного эффекта (очевидно, что внутриотраслевые эффекты при этом также не равны для разных уровней агрегирования).
При дальнейшем анализе результатов дезагрегирования исходных структур возникает дополнительный вопрос о значимости смещения оценок структурного эффекта, т.е. вопрос о том, можно ли пренебречь этим смещением или же оно может быть достаточно велико, чтобы инициировать принципиально различные результаты и выводы. Покажем на конкретном примере, что таким смещением оценок, вообще говоря, пренебречь нельзя, так как при этом возможно изменение характера структурных сдвигов.
Пусть в N–отраслевой структуре происходят изменения только двух долей: SN–1,t и SN,t, dSN–1,t/dt=–dSN,t/dt, dSN–1,t/dt>0, которые индуцируют трудосберегающий характер структурных сдвигов, т.е. структурный эффект .png) >0, где
>0, где
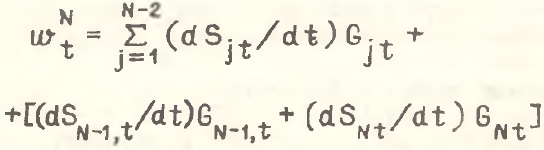 (3)
(3)
Так как первое слагаемое правой части формулы (3) равно нулю, то .png) >0 только в случае, если GN–1,t>GNt.
>0 только в случае, если GN–1,t>GNt.
Теперь рассмотрим ту же структуру, где первая отрасль дезагрегируется на две подотрасли с соответствующими долями Sʹ1t,.. Sʺ1t и производительностями Gʹ1t, Gʺ1t. При этом имеют место следующие сдвиги между подотраслями: dSʹ1t/dt>0, dSʹ1t/dt=–dSʺit/dt, так что удельный вес первой отрасли N – отраслевой структуры не изменяется. Тогда структурный эффект 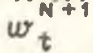 будет равен
будет равен
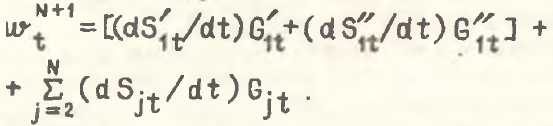 (4)
(4)
Чтобы выражение в квадратных скобках в разложении (4) было меньше нуля, необходимо, чтобы Gʹ1t<Gʺ1t. Так как второе слагаемое правой части формулы (4) равно структурному эффекту .png) и, если Gʹ1t<Gʺ1t, для того, чтобы
и, если Gʹ1t<Gʺ1t, для того, чтобы .png) <0, должно выполняться условие
<0, должно выполняться условие
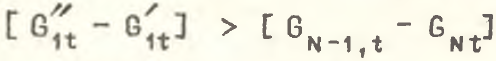 (5)
(5)
т.е. необходимо, чтобы разница между производительностями труда в подотраслях была больше, чем разница между производительностями труда в исходных отраслях, что на практике наблюдается довольно часто.
Таким образом, в случае GN–1,t>GNt и Gʹ1t<Gʺ1t и достаточной структурной неравномерности развития экономики, обеспечивающей выполнение условия (5), структурный эффект для N–отраслевой структуры .png) >0, т.е. в данном случае структурные сдвиги имеют трудосберегающий характер, а для структуры уровня агрегирования N+1 структурный эффект
>0, т.е. в данном случае структурные сдвиги имеют трудосберегающий характер, а для структуры уровня агрегирования N+1 структурный эффект .png) <0, т.е. структурные сдвиги носят трудорасходующий характер. Иными словами, при данном дезагрегировании произошло принципиальное искажение оценок структурного эффекта, которым пренебречь нельзя.
<0, т.е. структурные сдвиги носят трудорасходующий характер. Иными словами, при данном дезагрегировании произошло принципиальное искажение оценок структурного эффекта, которым пренебречь нельзя.
Приведенные примеры показывают условность получаемых оценок структурных эффектов и свидетельствуют о необходимости четкого оговаривания, какой уровень иерархии экономики рассматривается и, следовательно, эффективность каких структурных сдвигов оценивается.
Исходя из вышеизложенного, можно сформулировать определения локальной и глобальной инвариантности (устойчивости) оценок структурного эффекта при преобразовании уровня агрегирования.
Локальная инвариантность структурного эффекта наблюдается при отсутствии смещения его оценок при переходе с одного, вполне определенного, уровня агрегирования N на другой, также вполне конкретный уровень агрегирования N̅. Формально условие локальной инвариантности можно записать следующим образом:
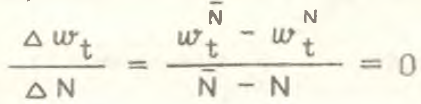 (6)
(6)
Глобальная инвариантность структурного эффекта наблюдается при отсутствии смещения его оценок при переходе с одного уровня агрегирования на любой другой уровень. Иначе говоря, при глобальной инвариантности оценка структурного эффекта для всех уровней агрегирования одинакова, т.е.  . Очевидно, что на практике глобальная инвариантность недостижима.
. Очевидно, что на практике глобальная инвариантность недостижима.
Из рассмотренных примеров вытекает, что если не учитывать возможного взаимного компенсирования межотраслевых ошибок, то условие, обеспечивающее локальную инвариантность оценок структурного эффекта, имеет следующий вид:
 (7)
(7)
при ограничении
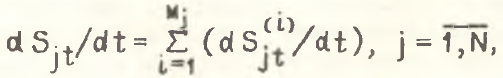 (8)
(8)
где i – индекс подотраслей, на которые дезагрегируется каждая отрасль j.
Условие (7) можно также получить следующим способом.
Проведем дезагрегирование отрасли j на Мj подотраслей и запишем для dGjt/dt разложение, аналогичное разложению (1),
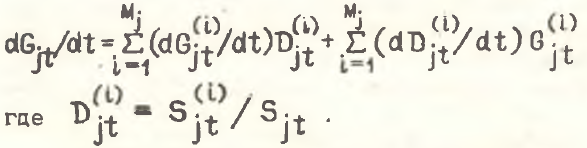 (9)
(9)
Подставив формулу (9) в разложение (1), путем тривиальных преобразований можно получить следующее уравнение:
 (10)
(10)
В случае инвариантности оценок структурных эффектов внутриотраслевые эффекты при исследуемом дезагрегировании должны быть равны (внутриотраслевые эффекты представлены первыми слагаемыми правых частей уравнений соответственно (1)–(10)). Отсюда автоматически вытекает условие, обеспечивающее инвариантность структурных эффектов и означающее равенство нулю выражения, стоящего в квадратных скобках в уравнении (10):
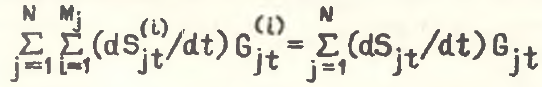 (11)
(11)
В более жесткой форме условие (11) превращается в условие (7).
Из уравнения (10) очевиден экономический смысл условия, обеспечивающего инвариантность оценок структурного эффекта при дезагрегировании; оценки инвариантны только в том случае, если структурные эффекты на более низких иерархических уровнях экономики отсутствуют.
Отметим, что все получаемые оценки эффективности структурных сдвигов справедливы относительно конкретного уровня агрегирования, в то время как идеальной и полной оценкой структурного эффекта является асимптотическая оценка 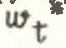 при бесконечно большом дезагрегировании экономической структуры, т.е. когда в разложении (1) N→∞ (оценка
при бесконечно большом дезагрегировании экономической структуры, т.е. когда в разложении (1) N→∞ (оценка .png) может быть также выражена в виде суммы бесконечного ряда структурных эффектов, возникающих на всех уровнях экономики):
может быть также выражена в виде суммы бесконечного ряда структурных эффектов, возникающих на всех уровнях экономики):
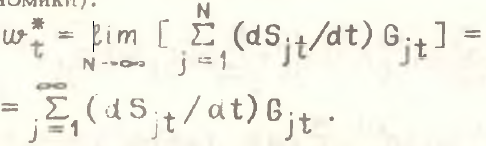 (12)
(12)
Однако в связи с невозможностью достижения предельной степени дезагрегирования исходных структур значение .png) на практике определить невозможно, и проблема оценки эффективности структурных сдвигов общего решения не имеет.
на практике определить невозможно, и проблема оценки эффективности структурных сдвигов общего решения не имеет.
Выше был рассмотрен процесс смещения оценок при дезагрегировании элементов исходных структур (т.е. экономическое дезагрегирование). Покажем, что аналогичные деформации оценок структурного эффекта могут происходить и при временном дезагрегировании.
Пусть за период времени dT=2dt≠0 структурные изменения в N–отраслевой структуре отсутствуют: dSjt/dT=0, j=1̅,̅N̅ .Тогда
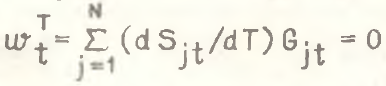 (13)
(13)
Рассмотрим два подпериода dt(1) и dt(2) исходного периода dT, причем dt(1)=dt(2)=dt. Пусть все доли Sjt неизменны в промежутках времени dt(1) и dt(2) за исключением SNt, при этом .png) , dSNt/dt>0. Тогда за первый интервал времени dt(1) имеем
, dSNt/dt>0. Тогда за первый интервал времени dt(1) имеем
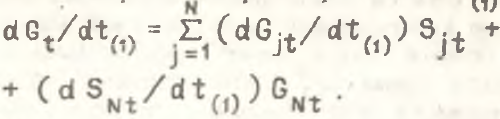 (14)
(14)
За второй интервал dt(2) имеем
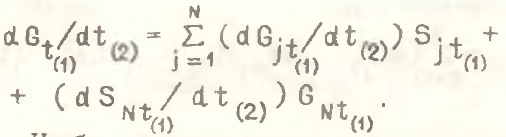 (15)
(15)
Чтобы определить прирост производительности за оба периода dt(1) и dt(2) и оценить суммарный структурный эффект за эти периоды, необходимо сложить уравнения (14) и (15). Тогда структурный эффект 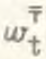 за период 2dt равен
за период 2dt равен
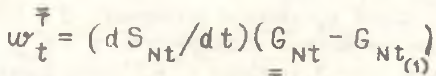 (16)
(16)
Для того чтобы .png) ≠0, необходимо, чтобы
≠0, необходимо, чтобы 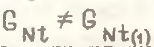 . В реальности производительность труда непрерывно изменяется, и в разные моменты времени ее показатели, как правило, не совпадают и, следовательно, на практике
. В реальности производительность труда непрерывно изменяется, и в разные моменты времени ее показатели, как правило, не совпадают и, следовательно, на практике .png) не будет равен нулю.
не будет равен нулю.
Таким образом, в случае .png)
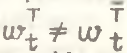 , т.е. происходит смещение оценок структурного эффекта при временном дезагрегировании.
, т.е. происходит смещение оценок структурного эффекта при временном дезагрегировании.
Данный пример достаточно важен, так как показывает, что искажение величины структурного эффекта возможно не только при переходе к новой экономической (например, отраслевой) номенклатуре, но и при анализе одной и той же структурной классификации за временные периоды разной степени детализированности.
Условие, обеспечивающее локальную инвариантность структурных эффектов при временном дезагрегировании, аналогично условию (11)
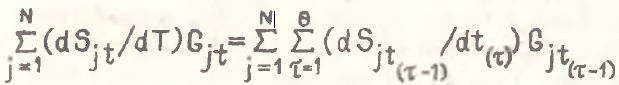 (17)
(17)
или в более жесткой форме
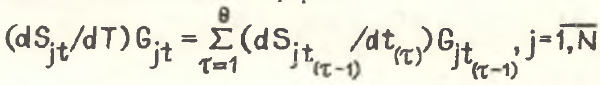 (18)
(18)
при ограничении
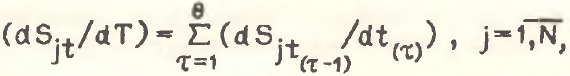 (19)
(19)
где 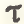 – индекс подпериодов времени, на которые дезагрегируется исходный временной интервал dT; θ – количество дезагрегированных подпериодов,
– индекс подпериодов времени, на которые дезагрегируется исходный временной интервал dT; θ – количество дезагрегированных подпериодов, .png) =1̅,̅θ.
=1̅,̅θ.
Экономический смысл условия (18) следующий: для инвариантности оценок структурного эффекта при временном дезагрегировании необходимо, чтобы на протяжении всего исходного временного интервала показатели производительности труда отраслей оставались постоянными. Другими словами, производительность труда в отраслях должна изменяться дискретно и мгновенно на границах анализируемого исходного временного периода, что в реальности абсолютно исключено, т.е. при временном дезагрегировании всегда будет иметь место смешение оценок структурного эффекта.
Рассмотренные вопросы, связанные с агрегированием и дезагрегированием экономических показателей, имеют достаточно важное значение при информационно–методическом обеспечении аналитических расчетов по определению эффективности структурных сдвигов в экономике. Отметим, что указанные вопросы разбирались для случая непрерывных величин; для дискретного случая ситуация аналогична рассмотренной.
Перейдем теперь к проблеме анализа воздействия конкретных видов структурных сдвигов на экономическую динамику. Так, на сегодняшний день получены формулы, позволяющие оценить влияние различных видов структурных изменений на динамику производительности общественного труда. В частности, данная проблем, решена для сдвигов в "отраслевых и региональных структурах национального дохода, занятости, основных производственных фондов, цен на конечную продукцию цен на производственные фонды (основной капитал) [1]. Вместе с тем самостоятельным и достаточно важным вопросом, не рассмотренным в литературе, является вопрос оценки воздействия сдвигов в отраслевой структуре заработной платы на динамику народнохозяйственной производительности труда. Действительно, диспропорции в структуре цен на рабочую силу оказывают влияние на эффективность ее использования и могут заметно деформировать тенденции темпов прироста производительности общественного труда.
Для получения искомых формул в целях оценки эффективности сдвигов в отраслевой структуре оплаты труда воспользуемся следующими тождествами:
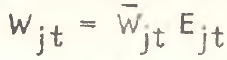 (20)
(20)
 (21)
(21)
где Wjt – фонд заработной платы отрасли j; W̅jt – среднеотраслевая величина заработной платы; Wt – фонд заработной платы материального производства в целом; W̅t – средняя заработная плата по материальному производству; Ejt – численность занятых в отрасли j; Et – численность занятых в материальном производстве.
Если уравнение (20) разделить на уравнение (21), то можно получить следующее выражение:
 (22)
(22)
Если ввести обозначения 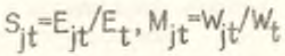 , M̅jt=W̅jt/W̅t, то выражение (22) может быть переписано в виде Sjt=Mjt/M̅jt, которое в темпах природы будет выглядеть следующим образом (здесь и далее звездочкой обозначаются темпы прироста соответствующих показа гелей в непрерывной форме):
, M̅jt=W̅jt/W̅t, то выражение (22) может быть переписано в виде Sjt=Mjt/M̅jt, которое в темпах природы будет выглядеть следующим образом (здесь и далее звездочкой обозначаются темпы прироста соответствующих показа гелей в непрерывной форме):
 (23)
(23)
Экономический смысл выражения (23) достаточно очевиден: скорость прироста доли отраслевого фонда оплаты труда (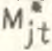 ) складывается из скорости прироста доли занятых в отрасли (
) складывается из скорости прироста доли занятых в отрасли (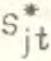 ) и скорости прироста отношения среднеотраслевой заработной платы к величине средней заработной платы в материальном производстве (
) и скорости прироста отношения среднеотраслевой заработной платы к величине средней заработной платы в материальном производстве (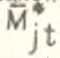 ).
).
С формальной точки зрения корректность выражения (23) очевидна. Однако с точки зрения правильности отображения причинно–следственных связей могут возникнуть сомнения в точности формы записи формулы (23) (альтернативный вариант записи (23): Mjt=.png) +
+.png) ). Действительно, возникает впечатление, что не
). Действительно, возникает впечатление, что не .png) труда зависит от относительного роста отраслевой заработной платы и зависит от
труда зависит от относительного роста отраслевой заработной платы и зависит от .png) и
и .png) , а
, а .png) определяется динамикой
определяется динамикой .png) и
и .png) , т.е. фонд оплаты зависит от относительного роста отраслевой заработной платы и увеличения доли занятых в отрасли. Однако, на наш взгляд, в нормально функционирующей экономической системе приток и отток трудовых ресурсов осуществляется в зависимости от финансового положения отрасли, т.е. от того, на сколько может быть увеличен отраслевой фонд оплаты труда для дополнительного привлечения рабочей силы. Более того, централизованная "подкачка" отраслевых фондов заработной платы и целенаправленные сдвиги в отраслевой структуре оплаты труда могут генерировать ускоренную межотраслевую миграцию кадров и служить одним из инструментов проведения структурной политики вообще и политики занятости в частности. Таким образом, и в формальном и в содержательном отношении выражение (33) записано верно.
, т.е. фонд оплаты зависит от относительного роста отраслевой заработной платы и увеличения доли занятых в отрасли. Однако, на наш взгляд, в нормально функционирующей экономической системе приток и отток трудовых ресурсов осуществляется в зависимости от финансового положения отрасли, т.е. от того, на сколько может быть увеличен отраслевой фонд оплаты труда для дополнительного привлечения рабочей силы. Более того, централизованная "подкачка" отраслевых фондов заработной платы и целенаправленные сдвиги в отраслевой структуре оплаты труда могут генерировать ускоренную межотраслевую миграцию кадров и служить одним из инструментов проведения структурной политики вообще и политики занятости в частности. Таким образом, и в формальном и в содержательном отношении выражение (33) записано верно.
Учитывая формулы (1) и (23), влияние сдвигов в отраслевой структуре занятости на темпы прироста производительности общественного труда (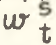 ) может быть записано в следующем вице:
) может быть записано в следующем вице:
 (24)
(24)
где 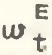 – влияние сдвигов в отраслевой структуре оплаты труда на темпы прироста народнохозяйственной производительности труда. Искомый эффект
– влияние сдвигов в отраслевой структуре оплаты труда на темпы прироста народнохозяйственной производительности труда. Искомый эффект .png) рассчитывается следующим образом:
рассчитывается следующим образом:
 (25)
(25)
Очевидно, что совместный анализ характеристик .png) и
и .png) достаточно важен, так как позволяет оценить различные стороны функционирования рынка труда. Так, если
достаточно важен, так как позволяет оценить различные стороны функционирования рынка труда. Так, если .png) позволяет оценить эффективность, как правило, только физического перемещения рабочей силы между отраслями, то
позволяет оценить эффективность, как правило, только физического перемещения рабочей силы между отраслями, то .png) дает возможность понять стоимостную сторону процессов, происходящих на рынке труда.
дает возможность понять стоимостную сторону процессов, происходящих на рынке труда.
Полученные формулы (23), (24) и (25) для оценки эффективности структурных сдвигов обладают рядом свойств, которые делают их использование достаточно удобным.
Во-первых, они позволяют получить общую характеристику функционирования рынка рабочей силы.
Во-вторых, данные формулы универсальны и могут быть использованы в аналитических целях на любом иерархическом уровне рассматриваемых экономических явлений, т.е. на любом уровне макро– и микропроцессор. В частности, они могут быть применены для анализа макроэкономических сдвигов, рассматриваемых в отраслевом и региональном разрезах.
В-третьих, полученные формулы обладают достаточной наглядностью и ясностью в смысле экономической интерпретации получаемых с их помощью результатов и отличаются чрезвычайной простотой с вычислительной точки зрения.
В-четвертых, формула (23) позволяет проанализировать такой структуроформирующий фактор, как цена рабочей силы. Иными словами, можно оценить влияние сдвигов в структуре заработной платы на направление, скорость и эффективность сдвигов в структуре занятости.
Рассмотрим теперь вопрос, связанный с координацией сдвигов, происходящих в различных структурах.
В случае рассмотрения сдвигов в отраслевых (региональных) структурах занятости, национального дохода и основных производственных фондов, которые являются наиболее значимыми с экономической точки зрения, возникает проблема оценки их взаимной согласованности. В данном случае интегрального показателя структурного эффекта, представляющего собой сумму частных структурных эффектов, недостаточно для оценки эффективности происходящих структурных изменений, так как даже при их общем положительном вкладе в прирост производительности общественного труда может наблюдаться ситуация, когда в одних секторах экономики (отраслях или регионах) может возникать избыток трудовых ресурсов, в то время как в других подразделениях будет наблюдаться ускоренный рост вакантных рабочих мест. Иными словами, возникает проблема увязки инвестиционных потоков в отрасли и регионы страны с миграционными потоками рабочей силы. Решение данной проблемы позволит обеспечить равновесие экономической системы и скоординировать между собой сдвиги на рынках рабочей силы, капиталов и товарном рынке.
В общем случае структурные сдвиги в экономике инициируются возникающими различиями в отраслевых уровнях нормы прибыли, что в свою очередь порождается изменениями в уровне эффективности производства в различных отраслях. В связи с этим, имея прогнозные значения основных показателей эффективности, можно сформулировать задачу определения возможных структурных сдвигов. Для решения поставленной задачи воспользуемся следующими формулами: Djt/Sjt=Ujt/Ut, Qjt/Djt=Hjt/Hj, Qjt/Sjt=Gjt/Gt, где Qjt доля чистой продукции отрасли j в произведенном национальном доходе; Djt – доля производственных фондов отрасли j в общем объеме основных производственных фондов по материальному производству; Ujt и Ut фондовооруженность соответственно отрасли j и материального производства; Hjt и Нt – фондоотдача отрасли j и материального производства в целом (в результате элементарных преобразований несложно убедиться в истинности приведенных формул). Тогда динамика отраслевых долей Djt, Sjt и Qjt и описывается следующими уравнениями:
.png) (26)
(26)
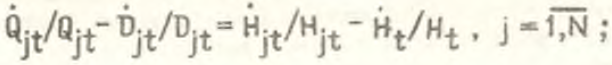 (27)
(27)
.png) (28)
(28)
Несмотря на простоту, система уравнений (26), (27) и (28) позволяет разрабатывать и согласовывать инвестиционную политику с политикой занятости и осуществлять регулирование уровня производства в отдельных народнохозяйственных звеньях. Для этого прежде всего необходимо иметь прогнозные значения отраслевых и народнохозяйственных показателей фондовооруженности, фондоотдачи и производительности труда. Определение последних возможно различными способами: от экстраполирования с помощью простейших трендовых моделей до эвристической процедуры прогнозирования на основе экспертных оценок, учитывающих имеющиеся резервы научно–технического прогресса в народном хозяйстве и его отраслях.
Имея оценки ожидаемых изменений фондовооруженности, фондоотдачи и производительности труда, можно разрабатывать структурную политику, исходя из имеющихся социально–экономических приоритетов и долговременных целевых установок. На этой стадии осуществляется прогноз прогрессивных сдвигов в структуре занятости. Тогда для определения рациональных сдвигов в отраслевой структуре основных фондов можно воспользоваться уравнением (26). Если по каким - либо причинам разработка инвестиционной политики является первичной, то, исходя из ожидаемых сдвигов в структуре капитальных вложений, а следовательно, и в структуре основных фондов, можно определить структуру занятости на перспективный период с учетом рациональной укомплектованности создающихся рабочих мест трудовыми ресурсами. В случае, если имеется достаточно обоснованный прогноз конъюнктурных изменений на товарном рынке в отраслевом разрезе, то из уравнений (27) и (28) можно определить необходимые сдвиги в структурах занятости и основных фондов.
В связи с тем, что из уравнений (26), (27), (28) можно получить только темпы прироста отраслевых полей Djt, Sjt и Qjt для их непосредственного вычисления необходимо пользоваться следующей формулой:
.png) (29)
(29)
где h – индекс прогнозного временного интервала; векторы Sjh и Qjh рассчитываются аналогичным образом.
Важную роль в проведении прогнозов играет учет имеющихся вакансий в отраслях и величин неудовлетворенного спроса на трудовые ресурсы. Такие данные в прогнозных исследованиях фигурируют в качестве запасов, в соответствии с которыми корректируются все экзогенные и эндогенные переменные.
Таким образом, фиксирование прогнозных значений одного из векторов {Djt}, {Sjt} и {Qjt} и экзогенное задание параметров фондоотдачи, фондовооруженности и производительности труда позволяет рассчитать возможные сдвиги в двух других структурах. Такой подход позволяет проводить серии имитационных экспериментов по взаимоувязке предполагаемых структурных сдвигов. Разумеется, полученные таким образом прогнозные траектории структурных изменений носят вероятностный характер и могут служить, лишь в качестве общей ориентации преобразования структуры экономики.
Одним из направлений исследования структурных сдвигов в экономике является определение скорости их протекания. В этих целях могут использоваться соответствующие расчетные формулы. Однако в связи с тем, что на сегодняшний день существуют и используются различные подходы к оценке интенсивности происходящих сдвигов, возникает проблема унификации данных подходов, ибо практикуемые методы могут давать принципиально различные результаты.
Охарактеризуем сущность данной проблемы.
Пусть имеется структура из N структурных элементов, в качестве которых могут выступать отрасли, регионы и другие секторальные подразделения экономики. При этом для любого интервала времени t элемент j народного хозяйства характеризуется удельным весом 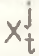 . Экономическая интерпретация показателя
. Экономическая интерпретация показателя .png) может быть различной в зависимости от рассматриваемых структур. В частности,
может быть различной в зависимости от рассматриваемых структур. В частности, .png) может обозначать долю ресурса отрасли j в общем объеме анализируемого вида ресурса по народному хозяйству (например, Sjt и Djt). Другой возможный вариант смысловой нагрузки
может обозначать долю ресурса отрасли j в общем объеме анализируемого вида ресурса по народному хозяйству (например, Sjt и Djt). Другой возможный вариант смысловой нагрузки .png) – доля продукта отрасли j в общем объеме произведенного продукта в народном хозяйстве (например, Qjt).
– доля продукта отрасли j в общем объеме произведенного продукта в народном хозяйстве (например, Qjt).
Таким образом, рассматриваемая структура в каждый момент времени характеризуется структурным вектором 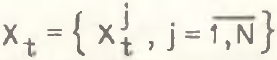 . Очевидно, что с течением времени исходная структура претерпевает изменения, и различные временные периоды характеризуются разными структурными векторами, т.е. имеют место структурные сдвиги. Задача заключается в определении скорости трансформации анализируемой структуры или, что то же самое, в определении интенсивности структурных сдвигов.
. Очевидно, что с течением времени исходная структура претерпевает изменения, и различные временные периоды характеризуются разными структурными векторами, т.е. имеют место структурные сдвиги. Задача заключается в определении скорости трансформации анализируемой структуры или, что то же самое, в определении интенсивности структурных сдвигов.
Рассмотрим основные подходы к решению данной задачи.
Практика структурных исследований и анализ специальной литературы показывают, что в данной области используются, как правило, три основных подхода.
Первый подход практикуется в исследованиях, проводимых в рамках Организации Объединенных Наций.
В соответствии с методическими указаниями ООН структурные векторы временных периодов t и t–1 представляют собой векторы, которые расположены в положительном ортанте N – мерного евклидова пространства. Так как .png) >0,
>0,  – j, t то процесс структурных сдвигов с геометрической точки зрения представляет собой перемещение вектора {X} закрепленного в начале системы координат, в пространстве положительного ортанта. В этом случае степень активности структурных, сдвигов за интервал времени [t–1,t] может быть охарактеризована величиной угла φ между векторами {Xt–1} и {Xt}, который в свою очередь однозначно определяется своим косинусом. Величина cos φ рассчитывается на основе формулы скалярного произведения векторов и выступает в качестве показателя скорости структурных сдвигов
– j, t то процесс структурных сдвигов с геометрической точки зрения представляет собой перемещение вектора {X} закрепленного в начале системы координат, в пространстве положительного ортанта. В этом случае степень активности структурных, сдвигов за интервал времени [t–1,t] может быть охарактеризована величиной угла φ между векторами {Xt–1} и {Xt}, который в свою очередь однозначно определяется своим косинусом. Величина cos φ рассчитывается на основе формулы скалярного произведения векторов и выступает в качестве показателя скорости структурных сдвигов .png)
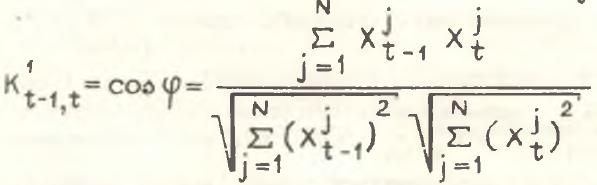 (30)
(30)
Так как структурные векторы расположены в положительном ортанте, то 1°≤φ≤90°, а 0≤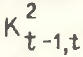 ≤1.
≤1.
Второй подход традиционен для отечественных исследований и в соответствии с ним коэффициент структурных сдвигов .png) , характеризующий скорость их протекания, равен
, характеризующий скорость их протекания, равен
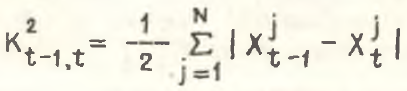 (31)
(31)
Из формулы (31) легко видеть, что 0≤.png) ≤1.
≤1.
Данный подход позволяет оценить не величину углового смещения структурного вектора, а степень абсолютного изменения его координат. В этом смысле показатель .png) , органически связан с величиной векторной нормы ||Хt–Xt–1|| и по сути дела представляет собой модификацию показателя длины вектора, заключенного между двумя точками {
, органически связан с величиной векторной нормы ||Хt–Xt–1|| и по сути дела представляет собой модификацию показателя длины вектора, заключенного между двумя точками {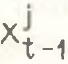 } и {
} и {.png) }.
}.
Таким образом, с геометрической точки зрения показатели .png) и
и .png) представляют собой совершенно различные характеристики. Очевидно, что в общем случае показатели
представляют собой совершенно различные характеристики. Очевидно, что в общем случае показатели .png) и
и .png) могут давать прямо противоположные результаты. Однако, в связи с наличием ограничительных условий
могут давать прямо противоположные результаты. Однако, в связи с наличием ограничительных условий 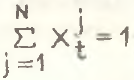 ,
, 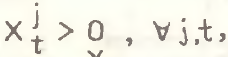 накладываемых на удельные веса Xt, возможное противоречие между показателями
накладываемых на удельные веса Xt, возможное противоречие между показателями .png) и
и .png) снимается, ибо структурные векторы могут перемещаться только внутри сегмента N – мерного шара, радиус которого равен единице, а центр совпадает с началом координат; данный сегмент ограничен положительным ортантом. Вместе с тем взаимная деформация оценочных траекторий, полученных с помощью коэффициентов
снимается, ибо структурные векторы могут перемещаться только внутри сегмента N – мерного шара, радиус которого равен единице, а центр совпадает с началом координат; данный сегмент ограничен положительным ортантом. Вместе с тем взаимная деформация оценочных траекторий, полученных с помощью коэффициентов .png) и
и .png) остается и затрудняет их сопоставимость.
остается и затрудняет их сопоставимость.
Третий, нетрадиционный, подход, практикуемый в отечественных исследованиях[2], основан на использовании следующего коэффициента  , оценивающего скорость происходящих структурных изменений:
, оценивающего скорость происходящих структурных изменений:
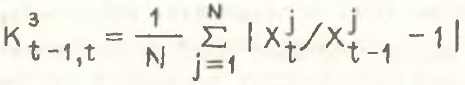 (32)
(32)
Данный подход тесно связан с предыдущим. Однако в отличие от него он основан на использовании не абсолютных скоростных характеристик (приростов), а относительных (темпов прироста). Такой подход с экономической точки зрения представляется более правомерным, так как именно относительные изменения структурных долей характеризуют значимость происходящих сдвигов.
Вместе с тем показатель .png) имеет существенный недостаток в связи с тем, что он, вообще говоря, не имеет верхней границы роста. Теоретически он заключен в интервалах
имеет существенный недостаток в связи с тем, что он, вообще говоря, не имеет верхней границы роста. Теоретически он заключен в интервалах
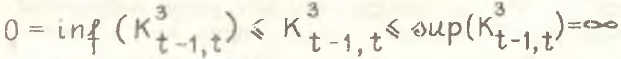 (33)
(33)
Данный факт позволяет говорить о принципиальной несопоставимости результатов, полученных с помощью показателей .png) и
и .png) (
(.png) ).
).
Несложно убедиться также, что при определенном наборе структурных долей и соответствующих изменениях данного вектора во времени можно получить принципиально различные результаты с помощью показателей .png) и
и .png) . Например, в случае, когда
. Например, в случае, когда .png) растет,
растет, .png) может убывать, и наоборот.
может убывать, и наоборот.
В общем случае с теоретической точки зрения ни одному их трех рассмотренных подходов к расчету скорости структурных сдвигов не может быть отдано явное предпочтение по сравнению с другими, так как все они достаточно корректны и эффективны. Кроме того, все указанные подходы многократно апробированы в аналитических исследованиях на реальных статистических данных и дали вполне удовлетворительные результаты. Вместе с тем каждая из расчетных формул (30), (31) и (32) имеет свои специфические недостатки.
Таким образом, в связи с наличием альтернативных подходов к оценке скорости структурных сдвигов в экономике анализ получаемых количественных результатов должен включать указание используемого метода.
Однако помимо проблемы смещения оценок скорости структурных сдвигов при использовании различных расчетных формул возникает дополнительная проблема смещения оценок при дезагрегировании экономических структур. Данная проблема аналогична рассмотренной выше при анализе эффективности структурных изменений. В частности, если каждая отрасль j исходной структуры уровня агрегирования N дезагрегируется на Mj элементов так, что вновь полученная структура имеет уровень агрегирования N̅, то условие инвариантности оценок скоростных характеристик .png) в общем виде выглядит следующим образом:
в общем виде выглядит следующим образом:
 (34)
(34)
В более жесткой форме условие (34) имеет вид
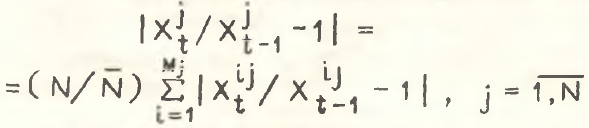 (35)
(35)
Здесь, как и ранее, i обозначает индекс подотраслей, на которые дезагрегируется каждая базовая отрасль j.
Для показателей .png) и
и .png) условия инвариантности аналогичны.
условия инвариантности аналогичны.
Экономический смысл формул (34) и (35) очевиден и не требует комментариев. Отметим только, что при переходе с одного уровня агрегирования экономической структуры на другой условия (34) и (35) практически всегда нарушаются.
[1] Подробнее об этом см. сб.: Концепция занятости в условиях социально ориентированной экономики. М., изд. НИЗИ при Госплане СССР, 1990, с.94.
[2] См. сб.: Концепция занятости в условиях социально ориентированной экономики. М., изд.НИЭИ при Госплане СССР, 1990, с.94.
Официальная ссылка на статью:
Балацкий Е.В., Лаврентьева О.В. Методические вопросы анализа структурных сдвигов в экономике и занятости/ В сб.: Занятость и экономическая реформа. М.: НИЭИ, 1992. С.177–198.