В последнее время в отечественной экономической литературе появилось большое число работ, посвященных формальной теории налогов [1–10]. В большинстве из них поднимается вопрос о существовании кривой А.Лаффера и ее свойствах. Вместе с тем в отношении лафферовых эффектов до сих пор остаются не только серьезные теоретические пробелы, но и просто-напросто методологические предрассудки, которые, хотя и лежат на поверхности явления, редко учитываются в конкретных исследованиях. Подобное положение вещей не позволяет, с одной стороны, сформулировать четкие концептуальные положения теории налогов, а, с другой – количественно оценить точки Лаффера для реальной экономики. Ниже мы последовательно докажем, что в рамках оптимизационного подхода возникает принципиальная неоднозначность и, как правило, множественность (неединственность) лафферова эффекта. Указанное явление порождается неясностью в отношении экономических критериев оценки производственной деятельности предприятий и фискальной политики государства. Кроме того, нами будут систематизированы многие фискальные эффекты в рамках единой методологии исследования.
Критерии производственной деятельности предприятий
Некоторые современные представления о кривой Лаффера раскрыты в [9]. В данной работе будут сформулированы дополнительные методологические принципы, которые необходимо учитывать при отыскании точек Лаффера.
В соответствии с оптимизационным подходом, доминирующим в теории налогов, методология анализа фискальных эффектов базируется на четком разделении двух типов экономических субъектов. Первый – предприятия, ведущие производственную деятельность, активность которых зависит от их технологических особенностей (ресурсоемкости, трудоемкости и т.д.), рыночных характеристик (цен, заработной платы и т.д.) и налогового климата (уровень налоговых ставок). Второй – государство, проводящее фискальную политику, результативность которой зависит от уровня налоговых ставок и величины налоговой базы, то есть производственной активности предприятий. При этом эффективность функционирования фирм и фискальной системы государства может оцениваться исходя из различных критериев, каждый из которых, вообще говоря, предполагает создание своей собственной экономической теории. Рассмотрим данный вопрос более подробно.
Классические оптимизационные модели теории фирмы предполагают максимизацию величины прибыли путем варьирования объемов производства x. При этом в качестве критерия эффективности могут выступать показатели чистой π1 и балансовой π2 прибыли:
1.1 π1(x)→max
1.2.π2(x)→max
Подобные критерии хорошо воспроизводят реальную ситуацию, если мы имеем дело с фирмой, управление которой осуществляется ее персонифицированным собственником. Однако даже в этом случае при определенных обстоятельствах более активным и важным может оказаться критерий максимизации объемов выпуска q:
1.3. q(x)→max
Такое положение характерно для предприятий, стремящихся к монополизации рынка сбыта и усилению позиций за счет расширения своих финансовых возможностей.
Можно сформулировать и другие аналогичные критерии. Например, в ряде случаев руководство фирмы в качестве главного ориентира рассматривает минимизацию налоговых платежей T:
1.4. T(x)→min
Разумеется, в реальности все оптимизационные задачи (1.1)–(1.4) сопровождаются системой ограничений. Более того, задачи фирм носят многокритериальный характер. Однако для нас в данной работе важно другое, а именно: какой критерий является главенствующим в производственно-финансовой стратегии предприятия. В этом смысле все критерии (1.1)–(1.4) представляют собой абсолютные величины, которые в общем случае генерируют различные оптимальные производственные программы xopt. Последние в свою очередь по-разному зависят от налоговых ставок, что влечет различную функциональную связь между фискальными поступлениями государства и ставками налогов. Этот момент является кардинальным во всем последующем анализе.
Несмотря на кажущуюся очевидность, естественность критериев (1.1)–(1.4) весьма сомнительна. Так, например, с точки зрения инвестора, который собирается вложить свои средства в действующее предприятие, абсолютное значение прибыли не имеет никакого смысла – его интересует доход на капитал, то есть относительные характеристики прибыльности производственного объекта. Такие интересы могут быть отражены показателем рентабельности:
2.1.π1(x)/R(x) →max
где R(x) - приведенные затраты.
В условиях, когда инвестор имеет дело с акционерной формой собственности, его в первую очередь интересует размер дивидендов:
2.2. (1–g)π1(x)/G→max
где g – доля прибыли, пускаемой на расширение производства; G – объем акционерного капитала.
В условиях конкуренции частного капитала за наиболее прибыльные сферы его приложения для собственника производства важно, какую долю составляет экспроприируемая им чистая прибыль от произведенной продукции:
2.3. π1(x)/q(x)→max
При развитом фондовом рынке, высокой инфляции и сильной конкуренции относительные критерии (2.1)–(2.3) играют значительно большую роль в формировании производственной программы предприятий, нежели критерии (1.1)–(1.4). При выборе между абсолютными и относительными критериями эффективности, на наш взгляд, предпочтение следует отдавать второй группе критериев. Во всяком случае их использование в анализе свидетельствует о плодотворности такого подхода [11–12]. Конкретные формы финансовых критериев могут быть сколь угодно разнообразными. Однако это не столь важно, важен сам принцип их множественности и неоднозначности.
Критерии фискальной политики государства
Неясность в отношении критериев эффективности экономической деятельности хозяйственных единиц усугубляется существующей альтернативностью в отношении оценки результативности фискальных мероприятий государства. Здесь можно выделить четыре различных подхода.
Первый подход предполагает отыскание только одной точки Лаффера для конкретного вида налоговых поступлений. Например, государство максимизирует объем налога на добавленную стоимость относительно его ставки; другие налоговые ставки предполагаются заданными и фиксированными. Подобная постановка задачи вполне реалистична, если учесть, что налоговые изменения носят, как правило, селективный характер и касаются только одного или нескольких видов фискальных ставок. Формально указанный критерий выглядит следующим образом:
3.1. Ti(hi)→max
где hi – ставка i–го налога; Ti – налоговые сборы i–го типа.
Второй подход подразумевает оптимизацию всей массы налоговых сборов при варьировании ставки лишь одного вида налога. Такой способ учитывает перекрестное взаимное влияние налогов:
3.2. 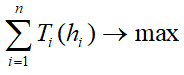
Третья фискальная стратегия государства предполагает максимизацию конкретного вида налоговых сборов при манипулировании всеми (или несколькими) налоговыми ставками одновременно:
4.1. 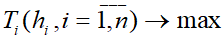
Подобная задача имеет ограниченную сферу действия и применяется, как правило, в аналитических расчетах.
Четвертый, обобщенный, подход ориентирован на достижение максимума всей суммы фискальных поступлений при задействовании всей совокупности налоговых параметров:
4.2. 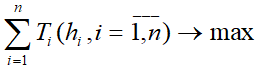
Критерии (3.1)–(4.2) являются абсолютными и традиционны для теории налогов. Однако в ряде случаев могут использоваться относительные показатели. Так, например, для государства большое значение имеет собираемость налогов, что равносильно макисимизации доли фискальных сборов в валовом внутреннем продукте. В этом случае критерий (3.1), например, принимает вид:
5.1. 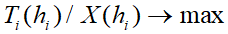
где X – объем валового внутреннего продукта. Аналогичные выражения могут быть записаны и для критериев (3.2), (4.1) и (4.2).
Здесь, как и в предыдущем разделе, мы показали неоднозначность и неочевидность постановки задачи по отысканию точек Лаффера. Для каждого из указанных критериев может строиться своя фискальная теория, что в вычислительном плане приводит к возникновению альтернативных точек Лаффера.
Анализ производственных стратегий предприятий
В данном разделе мы не будем проводить детальный разбор производственных стратегий фирм для всех возможных финансовых критериев, так как это заняло бы слишком много места без каких-либо серьезных теоретических обобщений. В связи с этим ограничимся только двумя наиболее существенными и репрезентативными случаями, а именно: критериями максимизации чистой прибыли и нормы прибыли.
В упрощенной форме чистая прибыль предприятия p может быть представлена в виде:
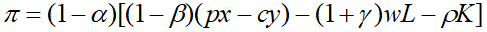 (1)
(1)
где x – объем выпускаемой предприятием продукции в натуральном выражении; p – средняя цена единицы выпускаемой продукции; y – оборотные фонды предприятия (сырье и материалы); c – средняя цена единицы оборотных средств; L – численность занятых на фирме; w – средняя заработная плата персонала; K – объем основного капитала в стоимостном выражении; ρ – норма амортизации; α – налог на прибыль; β – налог на добавленную стоимость; γ – социальные начисления на заработную плату.
Введем в рассмотрение показатель “текущей” нормы прибыли (рентабельности) r как отношение чистой прибыли к текущим издержкам производства R: r=π/R, где R=cγ+ρK+wL(1+γ). Дальнейший анализ сконцентрируем на двух задачах безусловной оптимизации:
π(x)→max (2)
r(x)→max (3)
Задача (2) соответствует традиционной гипотезе всей современной экономической теории и отражает стремление собственника производства к максимальному обогащению в заданных условиях. Подобный критерий можно классифицировать как ортодоксальный, который, на наш взгляд, слишком упрощенно воспроизводит реальность. Задача (2) принципиально статична, так как фиксирует стратегию производителя в жестко заданных условиях, когда фирма является абсолютно автономной экономической единицей и существуют непреодолимые барьеры выхода предпринимателя во внешний мир. Задача (3), наоборот, внутренне динамична, так как все финансовые переливы в экономике происходят в целях максимизации нормы прибыли на вложенный капитал, которая в свою очередь “конкурирует” с такими общезначимыми микро– и макропараметрами, как курсы акций и дивиденды действующих предприятий, процент по депозитам, процент по государственным ценным бумагам, процент за кредит и т.д. Возможность выбора одного из альтернативных путей вложения финансовых средств и предопределяет всеобщую значимость показателя нормы прибыли. В качестве последнего мы используем наиболее простую конструкцию – r.
Задачи (2) и (3) различаются не только с содержательной, но и с методологической точки зрения. Так, если абсолютный показатель чистой прибыли принципиально линеен и прост, то относительный показатель рентабельности является нелинейным и по своему внутреннему наполнению гораздо сложнее.
Задачи (2) и (3) генерируют различные оптимальные планы, которые не сводимы друг к другу. Если ввести в рассмотрение показатели эластичности затрат по выпуску θ=(x/y)(dy/dx), η=(x/L)(dL/dx), λ=(x/K)(dK/dx), то 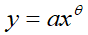 ,
, 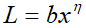 ,
, 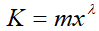 , где α, b и m – константы, зависящие от начальных условий. Используя линейную аппроксимацию степенных функций, из условия первого порядка для (2)
, где α, b и m – константы, зависящие от начальных условий. Используя линейную аппроксимацию степенных функций, из условия первого порядка для (2)
dπ/dx=0 (4)
несложно получить выражение для оптимального объема производства x0 [1]:
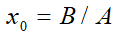 (5)
(5)
где
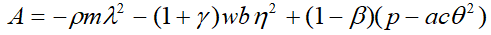 (6)
(6)
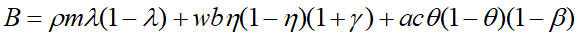 (7)
(7)
Обсудим получившийся результат. Если выполняется закон убывающей предельной отдачи производственных факторов (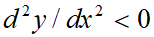 ;
; 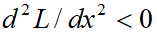 ;
; 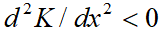 ), то θ<1; η<1; λ<1. Отсюда автоматически вытекают неравенства
), то θ<1; η<1; λ<1. Отсюда автоматически вытекают неравенства 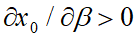 ;
; 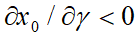 . Таким образом, увеличение ставки налога на добавленную стоимость и уменьшение ставок социальных начислений оказывает стимулирующее воздействие на производство безотносительно к экономическим условиям, в которых функционирует фирма. Кроме того, из (5) следует, что налог на прибыль вообще совершенно нейтрален и его увеличение никак не влияет на производственную активность предприятия. Все эти три вывода представляются весьма спорными. По-видимому, в данном случае мы имеем дело с логической ловушкой, которая может служить если не доказательством, то по крайней мере хорошей иллюстрацией бесперспективности использования в теории налогов показателя чистой прибыли в рамках оптимизационной схемы.
. Таким образом, увеличение ставки налога на добавленную стоимость и уменьшение ставок социальных начислений оказывает стимулирующее воздействие на производство безотносительно к экономическим условиям, в которых функционирует фирма. Кроме того, из (5) следует, что налог на прибыль вообще совершенно нейтрален и его увеличение никак не влияет на производственную активность предприятия. Все эти три вывода представляются весьма спорными. По-видимому, в данном случае мы имеем дело с логической ловушкой, которая может служить если не доказательством, то по крайней мере хорошей иллюстрацией бесперспективности использования в теории налогов показателя чистой прибыли в рамках оптимизационной схемы.
Теперь исследуем оптимальное решение задачи (3). Вместо уравнения оптимальности (4) имеем:
dπ/dx=r(dR/dx) (8)
Отсюда вытекает, что оптимальный план (3) x0 может быть выражен формулой:
x0=(B+δ)/A (9)
где δ=r(dR/dx)>0. Следовательно, x0> x0. Данный факт имеет большое теоретическое значение, так как в соответствии с ним критерий максимизации нормы прибыли порождает более высокий оптимальный уровень производства, чем критерий максимизации абсолютной массы прибылей. Таким образом, критерий (3) с позиции общественного благосостояния является более предпочтительным, нежели (2). Соответственно, все формулы, полученные из (2), и все экономические теории, базирующиеся на критерии (2), дают систематически заниженные оценки уровня производства и многих других экономических переменных.
Предположим, что руководство предприятия ориентируется на некий средний, нормальный уровень нормы прибыли r*, который поддерживается постоянным и обеспечивается объемом выпуска x0:
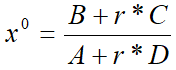 (10)
(10)
где
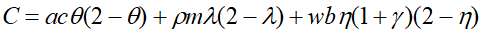 (11)
(11)
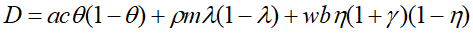 (12)
(12)
Учитывая A, B, C, D>0, из (10) вытекает, что
∂x0/∂r*>0, если AC–BD>0 (13)
Условие (13) неочевидно и его выполнение зависит от технологических характеристик предприятия, налоговых ставок и рыночной среды. При благоприятном стечении обстоятельств рост нормы прибыли ведет к повышению производственной активности экономического объекта; в противном случае позитивные сдвиги в уровне рентабельности могут вызвать производственную рецессию.
Выпишем оптимальное решение для (3) в явной форме, используя прежнюю процедуру линеаризации:
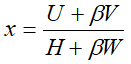 (14)
(14)
где
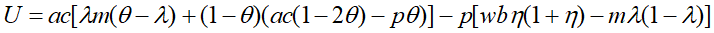 (15)
(15)
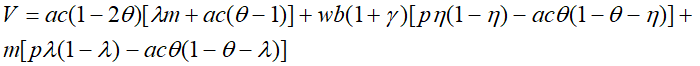 (16)
(16)
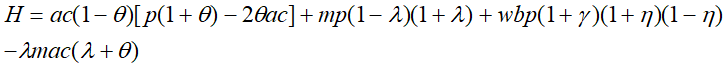 (17)
(17)
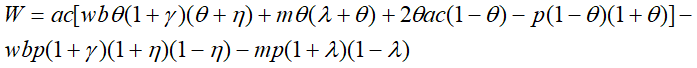 (18)
(18)
Из выведенных формул вытекает, что
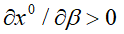 (19)
(19)
при выполнении условия
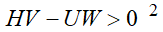 (20)
(20)
Таким образом, если производственные параметры предприятия вписываются в (20), то рост налога на добавленную стоимость подстегивает выпуск; если условие (20) нарушается, то его увеличение оказывает дестимулирующее воздействие на производственную активность фирмы.
Точки Лаффера первого рода
Во избежание путаницы введем некоторые определения. В частности, налоговые ставки, при которых достигается максимум оптимального объема производства предприятия, будем называть точками Лаффера первого рода. Последние в свою очередь могут быть автономными, получающимися при фиксации остальных налоговых ставок, и синхронными, которые отыскиваются одновременно. Для задач (2) и (3) автономные точки Лаффера 1-го рода отсутствуют.
Автономные точки Лаффера 1-го рода, получаемые из условия типа (19), соответствуют ситуации, когда происходит проверка только одного вида налога на оптимальность. Если же государственные органы оптимизируют всю налоговую систему одновременно, то условие (19) записывается для всех налогов, после чего решается получившаяся система уравнений. Так, например, для задачи (2) подобная система имеет вид: ∂x0/∂β=0; ∂x0/∂γ=0. Решения этой системы β* и γ* представляют собой синхронные точки Лаффера 1-го рода. Выкладки показывают, что, например, для критерия (2) подобные точки существуют и имеют вид:
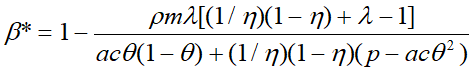 (21)
(21)
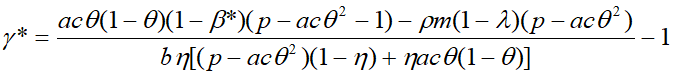 (22)
(22)
Таким образом, совместное действие нескольких налоговых ставок, как правило, ведет к возникновению лафферова эффекта. Так, например, точка β* является точкой перегиба на производственной кривой, если ставка социальных начислений находится на уровне γ* и, наоборот. В ряде случаев для достаточно сложных производственных критериев производственные кривые x(β) и x(γ) могут иметь несколько “горбов”. Это означает, что при оптимальной настройке всех налогов, кроме одного, последний будет оказывать различное влияние на производственную активность предприятия на различных участках кривой выпуска. Сказанное позволяет по-новому взглянуть на роль налогов в стимулировании экономического роста.
Роль инфляции в формировании точек Лаффера
В работе [5] рассматривался чрезвычайно важный эффект, когда рост цен ведет к изменению величины точки Лаффера. Однако методология анализа, используемая в [5], представляется неудовлетворительной по целому ряду причин. Наиболее уязвимым местом подхода, развитого в [5], является способ отражения структурной инфляции. В связи с этим покажем, каким образом эффект инфляционного сдвига точки Лаффера вписывается в развитую выше теоретическую схему, подчеркнув ее методические преимущества.
Из формул (21) и (22) видно, что одной из групп факторов, формирующих величину синхронных точек Лаффера, являются цены готовой продукции и сырья, а также заработная плата: c, p и w. Пусть в начальный момент времени точки Лаффера определяются в соответствии с (21) и (22). Определим точки Лаффера через период времени 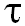 , в течение которого среднемесячные индексы роста c, p и w составляли I, J и Z, соответственно. Предположим, что за период
, в течение которого среднемесячные индексы роста c, p и w составляли I, J и Z, соответственно. Предположим, что за период .png) технологические характеристики фирмы не изменяются, то есть сдвиги затрагивают только ценовую среду, которая является особенно динамичной в рыночных условиях. В общем случае индексы I, J и Z не равны. Тогда новые значения точек Лаффера
технологические характеристики фирмы не изменяются, то есть сдвиги затрагивают только ценовую среду, которая является особенно динамичной в рыночных условиях. В общем случае индексы I, J и Z не равны. Тогда новые значения точек Лаффера 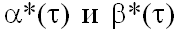 для предприятия будут определяться по формулам:
для предприятия будут определяться по формулам:
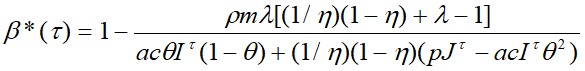 (23)
(23)
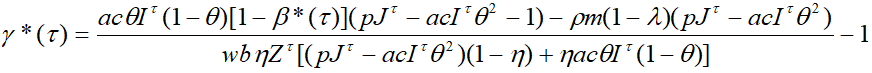 (24)
(24)
.png)
Рис.1. Инфляционное смещение точки Лаффера 1-го и 2-го рода.
Сравнивая формулы (23) и (24) с (21) и (22) легко видеть, что инфляционные тенденции, действительно, ведут к смещению точки Лаффера и деформированию производственной кривой Лаффера (графическая иллюстрация этого приведена на рис.1). Однако сказать что-либо определенное о направлении и силе происходящих сдвигов можно только по результатам пересчета новых точек Лаффера. Простота иллюстрации инфляционных эффектов очевидна. Кроме того, преимущество развитого нами подхода заключается в возможности учета тенденций не общего индекса–дефлятора, а структуры инфляции. В этой связи любопытно отметить, что даже при синхронном изменении цен c, p и w, когда I=J=Z, инфляционный сдвиг точек Лаффера все равно происходит, хотя, на первый взгляд, кажется, что сохранение структурного паритета между тремя видами цен гарантирует их устойчивость.
Налоговая политика государства.
Фискальные эффекты первого и второго рода
Как и в случае с производственными объектами, налоговая политика государства подразумевает различные критерии оценки ее эффективности. Не рассматривая их многочисленные разновидности, сконцентрируем внимание на главном варианте, предполагающем максимизацию налоговых сборов:
T(α,β,γ)→max (25)
где суммарная масса налоговых поступлений T складывается из трех видов фискальных платежей: налогов на прибыль, добавленную стоимость и заработную плату –
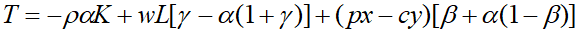 (26)
(26)
При изучении влияния сдвигов в уровне налоговых ставок на величину фискальных сборов следует иметь в виду, что общий фискальный эффект расщепляется на два субэффекта (для определенности будем рассматривать налог на добавленную стоимость):
∂T/∂β=(∂T/∂x)(∂x/∂β) (27)
В правой части уравнения (27) стоит общий фискальный эффект, применительно к которому строится классическая кривая А.Лаффера. Учитывая, что сдвиг налоговой ставки опосредованно влияет на массу фискальных поступлений, в правой части (27) отражена двухступенчатость данного процесса. В соответствии с (27) можно отдельно рассматривать фискальный эффект первого рода ∂x/∂β, который показывает реакцию производства на увеличение ставки налога, и фискальный эффект второго рода ∂T/∂x, демонстрирующий изменение налоговой массы в результате роста объемов производства. Таким образом, общий фискальный эффект ∂T/∂β формируется как произведение эффектов первого и второго рода. При этом, если фискальный эффект первого рода учитывает финансово-воспроизводственный аспект деятельности предприятия, то эффект второго рода – структуру налогов и производственных затрат фирмы.
Методология “двухзвенного” анализа по формуле (27), несмотря на свою простоту, весьма плодотворна и эффективна. Так, например, из (27) вытекает, что рост ставки налога на добавленную стоимость в конкретных условиях может порождать отрицательный финансовый эффект первого рода при ∂x/∂β<0 при положительном эффекте второго рода ∂T/∂x>0 и, наоборот. Общий фискальный эффект в этом случае будет отрицательным. Таким образом, особую опасность при проведении государством налоговой политики представляет разнознаковость фискальных эффектов первого и второго рода.
Из предыдущего анализа ясно, что фискальный эффект первого рода может быть любого знака. Относительно эффекта второго рода, на первый взгляд, кажется, что он всегда должен быть положительным. Действительно, рост производства, как правило, ведет к расширению налоговой базы (данный тезис является исходным пунктом экономики предложения А.Лаффера), а это, в свою очередь, ведет к росту налоговой массы. Однако в реальности все обстоит далеко не всегда так. Покажем это на формулах. Из (26) следует, что
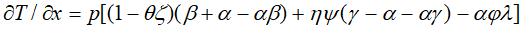 (28)
(28)
где 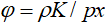 ;
; 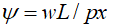 ;
; 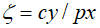 . Параметры φ, ψ и ζ задают структуру производственных затрат. Из (28) видно, что ∂T/∂x>0, если выполнено условие
. Параметры φ, ψ и ζ задают структуру производственных затрат. Из (28) видно, что ∂T/∂x>0, если выполнено условие
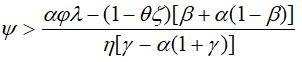 (29)
(29)
При ближайшем рассмотрении условие (29) оказывается достаточно содержательным и позволяет сделать некоторые важные выводы о рациональной системе налогообложения. В частности, для нашей трехналоговой схемы легко просматривается следующий макроэкономический принцип: для выполнения условия (29) достаточно, чтобы ставки налогов на добавленную стоимость и заработную плату были оба меньше ставки налога на прибыль. Действительно, при такой структуре ранжирования налоговых ставок правая часть (29) отрицательна и, следовательно, (29) автоматически выполняется. В противном случае истинность (29) оказывается под вопросом.
Таким образом, нами показано, что в общем случае фискальный эффект второго рода может быть любого знака. Данный факт чрезвычайно важен, так как при ∂T/∂x<0 любой рост производства будет разрушать государственный бюджет, что просто абсурдно и недопустимо. По всей видимости формирование структуры налоговых ставок должно начинаться с проверки условия (29). При этом следует отметить, что фискальный эффект второго рода не зависит от финансовых критериев производственных объектов и в этом смысле более универсален и однозначен, нежели фискальный эффект первого рода.
Точки Лаффера второго рода
Продолжая выбранную нами методологию классификации, определим точки Лаффера второго рода как налоговые ставки, при которых достигается максимальная величина налоговых поступлений. Применительно к налогу на добавленную стоимость условие существования лафферовой точки второго рода имеет вид: ∂T/∂β=0. Таким образом, равенство нулю фискального эффекта первого рода порождает точки Лаффера первого рода, а равенство нулю общего фискального эффекта генерирует точки Лаффера второго рода. Заметим, что наличие последних эквивалентно существованию традиционной кривой Лаффера. При этом такие точки также могут быть автономными, когда оптимизируется один вид налога, и синхронными, когда оптимизация идет по всем или нескольким видам налогов одновременно. Понятно, что в общем случае точки Лаффера первого и второго рода не совпадают, чем и обусловлено введение их в рассмотрение.
Учитывая разложение (27) ясно, что при отсутствии автономных точек первого рода точки второго рода все же могут существовать и определяются фискальным эффектом второго рода. Для налога на добавленную стоимость применительно к задаче (3) автономная точка Лаффера второго рода β** автоматически вытекает из условия ∂T/∂x=0, то есть
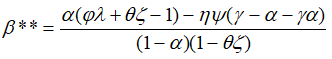 (30)
(30)
При наличии точек Лаффера первого рода ситуация резко усложняется благодаря возникновению множества критических точек, которые находятся в сложном соотношении. Подобные эффекты особенно актуальны при рассмотрении синхронных лафферовых точек второго рода.
В отношении инфляционного сдвига полученной нами автономной точки Лаффера второго рода β** ситуация достаточно проста. Так, например, в момент времени .png) данная точка смещается в точку β**(
данная точка смещается в точку β**(.png) ):
):
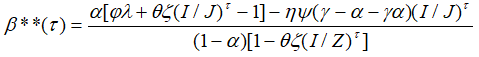 (31)
(31)
Из (31) видно, что при отсутствии структурной инфляции, то есть при I=J=Z, инфляционного смещения точки Лаффера второго рода не происходит.
Отметим, что в общем случае вместо (27) следует использовать соотношение
dT/dβ=∂T/∂β+(∂T/∂x)(dx/dβ) (32)
При такой форме учета фискальных эффектов анализ сильно усложняется и выходит за рамки данной статьи.
Прикладные расчеты
Полученные в ходе нашего исследования теоретические конструкции нуждаются в количественной апробации. Начнем с проверки условия (29) применительно к российской экономике. Для этого будем использовать данные таблицы 1 и таблицы 2. [3] Предварительно заметим, что в прикладных расчетах показатели эластичности затрат нами оценивались в дискретной форме следующим образом:
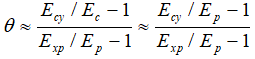 (33)
(33)
где Ecy – индекс роста объема материальных затрат в текущих ценах; Ec – индекс удорожания материальных затрат; Exp – индекс роста объема валового общественного продукта в текущих ценах; Ep – индекс инфляции (нами использовался индекс потребительских цен). Из-за нехватки данных предполагаем Ec= Ep. Для параметров λ и η ситуация аналогична.
Таблица 1.
Структура производственных затрат в российской экономике, %
|
Доля в валовом общественном продукте |
1991 |
1992 |
1993 |
1994 |
1991–1994 |
|
Оплаты труда (ψ) |
18,66 |
10,49 |
13,88 |
12,55 |
13,90 |
|
Материальных затрат (ζ) |
52,24 |
58,59 |
51,00 |
58,59 |
55,11 |
|
Амортизации (φ) |
8,21 |
4,70 |
7,90 |
5,10 |
6,48 |
Таблица 2.
Показатели эластичностей затрат по выпуску для российской экономики
|
Эластичность |
1991–1992 |
1992–1993 |
1993–1994 |
1991–1994 |
|
Труда по выпуску (η) |
2,20 |
0,04 |
0,33 |
0,86 |
|
Материальных затрат по выпуску(θ) |
0,87 |
1,40 |
2,20 |
1,49 |
|
Амортизации по выпуску (λ) |
0,93 |
–1,04 |
–1,67 |
–0,59 |
Анализ таблиц 1 и 2 показывает, что, во-первых, российская экономика характеризовалась чрезвычайной неустойчивостью развития. Это связано с переходным периодом, в течение которого происходила реструктуризация всего народного хозяйства страны, что выразилось в резких скачках всех структурных макропоказателей. Во-вторых, величины эластичности затрат по выпуску выходили за естественные границы, принимая значения больше единицы, а иногда, наоборот, отрицательные значения. Все это подводит к необходимости проведения усредненных расчетов за период 1991–1994 гг.
По аналогии с [8] налоговые параметры нами разнесены на два сценария (табл.3), один из которых льготный, другой – стандартный. Данные табл.3 соответствуют налоговому климату, сложившемуся на начало 1996 г.
Расчеты, проведенные по формуле (35), показывают, что в целом за 1991-1994 гг. в России были условия, которые гарантировали рост налоговых поступлений по мере расширения производства:
№1 (1991-1994 гг.) – условие (29) выполняется.
№2 (1991-1994 гг.) – условие (29) выполняется.
Теперь оценим по формуле (30) автономную точку Лаффера второго рода применительно к налогу на добавленную стоимость. Сценарные расчеты дали следующий результат:
№1 (1991-1994 гг.) – β** = 41.1%
№2 (1991-1994 гг.) – β** = 56.8%
Важно отметить, что указанные оценки действительно являются точками глобального максимума фискальной кривой только при положительном фискальном эффекте первого рода. Однако последнее маловероятно при столь высоких налоговых ставках, что позволяет говорить об отсутствии точек Лаффера для российской экономики анализируемого периода.
Обсуждение результатов
Проведенный анализ позволяет сформулировать концептуальное резюме в форме нескольких выводов.
I. Для повышения терминологической корректности нами введена классификация фискальных эффектов, которые подразделяются на эффекты первого и второго рода. Аналогичная классификация используется в отношении точек Лаффера и предполагает точки Лаффера первого и второго рода. Кроме того, дополнительно вводится понятие автономных и синхронных точек Лаффера. Все указанные фискальные эффекты и точки Лаффера функционально несопоставимы и в общем случае не сводимы друг к другу, чем, собственно говоря, и вызвано введение их в анализ.
Таблица 3.
Налоговые ставки для российской экономики, %
|
Сценарий расчета |
Ставки налога на |
||
|
Прибыль (α) |
Добавленную стоимость (β) |
Заработанную плату (γ) |
|
|
№1 |
20,0 |
10,0 |
41,0 |
|
№2 |
35,0 |
20,0 |
41,0 |
II. В работе показана принципиальная роль системы экономических критериев при определении величины фискальных эффектов и точек Лаффера на базе оптимизационного подхода. При этом финансовые критерии эффективности деятельности предприятий сказываются на величине фискального эффекта первого рода, в то время как экономические критерии результативности налоговой политики государства определяют величину фискального эффекта второго рода. В свою очередь фискальный эффект первого рода “отвечает” за формирование точек Лаффера первого рода, а фискальный эффект второго рода доминирует при определении точек Лаффера второго рода. В целом же конкретные количественные значения точек Лаффера являются во многом субъективными, так как получаются исходя из априори определенных целевых функций государства и экономических агентов. Данный тезис предполагает весьма критическое отношение ко всем расчетам точек Лаффера, базирующимся на оптимизационных моделях. По-видимому, при макрооценивании фискальных эффектов следует отдавать предпочтение методам расчета, основывающимся на дескриптивных моделях и схемах анализа.
III. Рассмотрение двух критериев экономической деятельности предприятия, предполагающих максимизацию чистой прибыли и нормы прибыли, показало, что роль налоговых ставок в формировании производственных стратегий предприятия не зависит от количественных значений налогов и целиком и полностью детерминируется технологическими особенностями фирмы и рыночной среды, в которой она функционирует. В зависимости от этого фискальный эффект первого рода может быть как отрицательным, так и положительным, а автономные точки Лаффера отсутствуют. Таким образом, действительный интерес для теории налогов имеет лишь знак фискального эффекта первого рода. В общем случае можно представить такой критерий деятельности фирмы, который будет приводить к возникновению автономных точек Лаффера первого рода; синхронные же точки Лаффера возникают практически всегда, что лишний раз доказывает необходимость их различия в экономическом анализе.
IV. Полученные количественные соотношения показывают, что оценить фискальный эффект второго рода с вычислительной точки зрения оказывается значительно легче, чем эффект первого рода. Можно также утверждать, что и степень субъективности в выборе фискального критерия государственной политики также меньше. Вместе с тем, именно фискальный эффект второго рода генерирует стационарные налоговые ставки, которые могут выступать в качестве автономных точек Лаффера второго рода. Отсюда вытекает довольно простой алгоритм определения таких точек. Сначала на основе анализа фискального эффекта второго рода определяется критическая налоговая ставка. Далее определяется знак фискального эффекта первого рода, в зависимости от чего делается вывод о том, является ли данная критическая налоговая ставка точкой Лаффера или нет. Следует отметить, что фискальный эффект второго рода в отличие от эффекта второго рода универсален для всех налогов, то есть не зависит от вида налоговых изъятий. При расчете синхронных точек второго рода ситуация сильно усложняется за счет возникновения целого каскада критических точек, порождаемых эффектами как первого, так и второго рода. В этом случае необходим аккуратный анализ по просеиванию получившихся критических точек по признаку их отнесения к точкам Лаффера. В результате такой процедуры вероятно появление нескольких точек второго рода, что означает (и это теоретически очень важно) существование многогорбой фискальной кривой. Подобная форма искомой кривой существенно корректирует наши представления о роли каждого налога в формировании доходов государства.
V. Чтобы на практике оценить степень субъективности различных финансовых критериев оценки деятельности экономических субъектов необходимо проводить расчеты по наиболее важным из них. Если в большинстве случаев знак фискального эффекта первого рода будет совпадать для различных критериев, то это позволит сделать вывод об инвариантности фискального эффекта первого рода относительно ключевых финансовых критериев, что, во-первых, будет свидетельствовать об определенной объективности оптимизационной схемы расчета, а, во-вторых, позволит выбрать один из финансовых критериев, который дает наиболее простой способ оценки точек Лаффера. В любом случае проблема инвариантности в данном случае решается с точностью до знака, что делает ее не слишком острой. В этом смысле фискальный эффект первого рода носит подчиненное значение, так как он не формирует величины точки Лаффера, а лишь определяет их наличие. Иными словами, финансовые критерии деятельности предприятий не влияют на численные значения искомых точек Лаффера.
Литература
[1] С.В.Алексашенко, Д.А.Киселев, П.М.Теплухин, Е.Г.Ясин. Налоговые шкалы: функции, свойства, методы управления (“Экономика и математические методы”. Т.25. Вып.3. 1989).
[2] Л.Е.Соколовский. Подоходный налог и экономическое поведение (“Экономика и математические методы”. Т.25. Вып.4. 1989).
[3] Л.Е.Соколовский. Налог на добавленную стоимость и предприятие, максимизирующее прибыль (“Экономика и математические методы”. Т.28. Вып.4. 1992).
[4] С.М.Мовшович, Л.Е.Соколовский. Выпуск, налоги и кривая Лаффера (“Экономика и математические методы”. Т.30. Вып.3. 1994).
[5] В.В.Капитоненко. Инфляционный сдвиг налоговой ставки на кривой Лаффэра (“Экономика и технология: межвузовский сборник научных трудов”. М.: РЭА. 1994).
[6] С.В.Гусаков, С.В.Жак. Оптимальные равновесные цены и точка Лаффера (“Экономика и математические методы”. Т.31. Вып.4. 1995).
[7] Э.Б.Аткинсон, Дж.Э.Стиглиц. Лекции по экономической теории государственного сектора. М.: Аспект Пресс. 1995.
[8] Е.В.Балацкий. Инфляционные налоги и экономический рост (“Экономика и математические методы”. Т.33. Вып.3. 1997).
[9] Е.В.Балацкий. Фискальное регулирование в инфляционной среде (“Мировая экономика и международные отношения”. №1. 1997).
[10] Е.В.Балацкий. Инфляционное равновесие и бюджетная сбалансированность (“Мировая экономика и международные отношения”. №3. 1997).
[11] Е.В.Балацкий. Дифференциальные свойства кривых спроса и предложения (“Мировая экономика и международные отношения”. №12. 1995).
[12] Е.В.Балацкий. Переходные процессы в экономике (методы качественного анализа). М. ИМЭИ. 1995.
[13] М.Я.Выгодский. Справочник по высшей математике. М. Физматгиз. 1963.
[1] Линеаризация степенных функций достигается за счет их разложения в ряд Тейлора с точностью до второго члена: 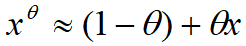 . Подобный переход обусловлен нелинейностью условий первого порядка относительно переменной x. В связи с этим все последующие формулы являются приближенными и способствуют установлению характера основных взаимосвязей. В дальнейшем будем подразумевать, что условие второго порядка d2π/dx2<0 выполнено и точка x0 – точка максимума.
. Подобный переход обусловлен нелинейностью условий первого порядка относительно переменной x. В связи с этим все последующие формулы являются приближенными и способствуют установлению характера основных взаимосвязей. В дальнейшем будем подразумевать, что условие второго порядка d2π/dx2<0 выполнено и точка x0 – точка максимума.
[2] При выводе (19) нами использовалась “усеченная” форма выражений для прибыли и затрат:
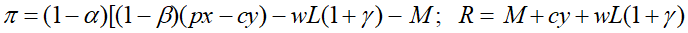
где M – амортизация. Соответственно далее показатель эластичности λ=(x/M)(dM/dx).
[3] Автор приносит искреннюю благодарность Л.А.Стрижковой и А.Е.Ивантеру за любезно предоставленную информацию, необходимую для формирования данных таблиц 1 и 2.
Официальная ссылка на статью:
Балацкий Е.В. Лафферовы эффекты и финансовые критерии экономической деятельности// «Мировая экономика и международные отношения», №11, 1997. С. 31–43.