1. Введение. Вряд ли будет большим преувеличением утверждение о том, что современная экономическая наука является преимущественно наукой об экономическом росте, который в свою очередь отождествляется с цивилизационным развитием. Такое значение феномена экономического роста связано со многими причинами, в числе которых лежит и тот факт, что он не является «естественным» природным режимом существования человечества, а насчитывает от силы 250–300 лет. До этого, на протяжении примерно 10 тыс. лет, человечество пребывало в режиме так называемой мальтузианской ловушки или ловушки бедности. Таким образом, смена экономического режима сама по себе представляет собой экстраординарное явление. По этому поводу имеется весьма симптоматичное высказывание Д. Норта: «Экономический рост был исключением, а правилом – стагнация и упадок…» [1, с. 193].

В словах Норта недвусмысленно заложено предположение, что в будущем человечество, скорее всего, снова вернется к режиму стагнации. Однако Норт не одинок в своем мнении. Например, Р. Лукас констатирует следующее: «Современные теории устойчивого роста… абстрагируются от изучения предложения земли и вообще от ограниченных ресурсов. Подобные теории могут объяснять и объясняют длинные экономические ряды достаточно хорошо, но это не сможет продолжаться долго»; «…Становится все более очевидным то, что наследие неравенства, побочный продукт роста, является исторически преходящим» [1]. Еще более категоричен Т. Пикетти, который считает, что представление о «нормальности» экономического роста с годовым темпом в 3–4% – это типичная «иллюзия как с исторической, так и с логической точки зрения» [2, с. 107]. Следовательно, многие авторитетные экономисты современности высказывают сомнения в продолжении длительного и интенсивного роста мирового производства.

В последнее время набирает обороты направление исследований, связанных с «концом роста». Например, Р. Хейнберг доказывает, что экономический рост достиг физического предела и на его пути стоит три непреодолимых препятствия: истощение важных природных ресурсов; ухудшение экологической обстановки; перенакопление государственной и негосударственной задолженности [3]. Тем самым мы стоим на пороге совершенно иного режима экономического развития, предполагающего не количественное увеличение массы благ, а их качественное усовершенствование.

Учитывая сказанное, цель статьи состоит в рассмотрении простой макромодели экономического роста, которая прольет дополнительный свет на механизм выхода из мальтузианской ловушки и перехода к режиму экономического роста, а также позволит определить те проблемы, с которыми придется столкнуться человечеству при возвращении к состоянию экономической стабильности. Данные вопросы непосредственно связаны с источниками и условиями роста, которые позволяют запустить ускоренное экономическое развитие. Новизна предложенного подхода состоит в рассмотрении экономического роста как следствия процесса круговорота капитала. Важным достоинством построенной модели является явная увязка темпов экономического роста с величиной рентабельности капитала.

2. Описание экономического роста: обзор ключевых идей. Исследования экономического роста настолько многочисленны и разнообразны, что охватить их полностью нет никакой возможности. В связи с этим рассмотрим лишь некоторые аспекты данной проблемы, которые имеют непосредственное отношение к дальнейшим модельным построениям.

Факторы экономического роста. Общая линия исследований факторов экономического роста была задана Р. Солоу еще в 1956 г. моделью, в которой совокупный выпуск зависел от объема капитала, трудовых ресурсов и технологического прогресса [4]. Последующие поколения экономистов уточняли модель Солоу за счет введения фактора человеческого капитала [5], затрат на исследования и разработки [6], степени вовлеченности страны в глобальную экономику [7] и т.п.

Изучение вклада основных факторов производства в рост экономики привело к осознанию значимости эластичности замещения труда капиталом как меры уровня развития всей экономической системы [8]. В частности, масштаб влияния этого параметра был использован для объяснения дисперсии среднедушевого дохода [9], различий в уровне экономического развития стран [10], а также направления технологической модернизации [11]. В целом, согласно неоклассической традиции, экономический рост представляет собой следствие процесса аккумулирования основного капитала [12]. На выборке из крупнейших мировых экономик за период с 1870 по 1979 гг. было установлено, что наибольший эффект от ускоренного накопления капитала наблюдается при догоняющем развитии, когда требуются обильные средства для запуска новых производств [13].

Подчеркнем, что уже ранняя модель Солоу базировалась на так называемом тождестве для валовых инвестиций, что в свою очередь позволило установить золотое правило накопления, зависящее от величины капиталовооруженности. На основе данных об американской экономике за 1909–1949 гг. Солоу показал, что рост ВВП в этот период детерминировался как технологическим прогрессом, так и увеличением капитала [14]. Таким образом, традиция описания экономического роста восходит к учету динамики накопления основного капитала. Этот тезис в дальнейшем будет использоваться в качестве отправного.

Учет технологического прогресса. Уже в самых ранних моделях роста был введен постулат о зависимости производительности труда от капиталовооруженности [15; 16; 17]. Более того, данная функциональная зависимость имела степенной вид с коэффициентом, меньшим 1. Одним из эмпирических подтверждений данного подхода служит сравнение динамики экономики США и Великобритании: в период с 1840 по 1910 гг. при сохранении приблизительно равных страновых значений совокупной факторной производительности в США наблюдался более быстрый рост производительности труда, что объясняется их почти полуторакратным превосходством в величине капиталовооруженности [18].

Позднее однофакторная модель успешно применялась в прикладных исследованиях. В частности, она использовалась с целью кластеризации отраслей экономики Китая по принципу достаточности капиталовооруженности [19]. Аналогичным образом на примере Китая была показана динамика зависимости производительности труда от капиталовооруженности на разных временных интервалах [20]. Похожая модель с учетом потока, а не запаса капитальных ресурсов была использована для оценки периодов избыточного инвестирования для марокканской экономики в период с 1970 до начала 2010–х гг. [21]. Таким образом, простота однофакторной модели не умаляет ее диагностической ценности и позволяет получить содержательные результаты.

Впоследствии большую популярность получила модель эндогенного технологического прогресса Агьона–Ховитта, в которой было дано теоретическое описание процесса смены разных поколений технологий [22; 23]. При этом степенная функция сохраняется, но дополнительно вводится специальный оператор технологического прогресса, учитывающий смену поколений производственных технологий [22]. Очередная эмпирическая проверка гипотезы о нелинейной связи производительности труда и капиталовооруженности была предпринята в 2020 г. и показала, что только в Канаде, США, России, Франции и Финляндии искомый степенной коэффициент значимо больше 1, что говорит о наличии в указанных странах технологического эффекта масштаба; в других государствах, попавших в выборку, данный эффект не обнаружен [24]. Следовательно, традиция описания экономического роста предполагает также и представление о степенной зависимости производительности труда от технологической оснащенности рабочего места, т.е. от капиталовооруженности производства; далее данный тезис будет взят на вооружение.

Выход из мальтузианской ловушки. Помимо моделирования экономического роста как такового, особый интерес представляет процесс перехода от многовековой перманентной депрессии к режиму экономического роста. Так, одна из первых моделей, изучающих стадии мальтузианской ловушки и условия выхода из нее на основе анализа зависимости между трудовыми ресурсами и реальной заработной платой, была предложена в 1980 году [25]. Впоследствии она была расширена и уточнена в исследованиях [26; 27; 28; 29]. Однако, пожалуй, наиболее фундаментальной работой в указанном направлении считается модель Арцруни–Комлоса, учитывающая взаимообусловленное демографическое и экономическое развитие Мир–Системы на протяжении последних 10 тыс. лет; преодоление мальтузианской ловушки, по мнению авторов, стало возможно в результате индустриальной революции, достаточного накопления капитала (темпы роста которого превышали 5% за декаду) и замедления темпов роста населения (не более 5% за декаду) [30].

Впоследствии моделирование процесса выхода из мальтузианской ловушки было продолжено в трудах как зарубежных [31; 32 и др.], так и отечественных исследователей [33; 34 и др.]. В этом отношении можно считать знаковой работу 2012 г. [35], в которой автор говорит о возможности двух способов преодоления мальтузианской ловушки: западные страны достигли этого путем разрушения традиционных институтов (общины) и перехода к более эффективным индивидуалистическим институтам, тогда как страны Азии смогли сохранить коллективные ценности и институты за счет их грамотной модернизации. Такая трактовка перехода к росту позволяет автору сделать весьма интересный прогноз: к странам, которые в будущем продемонстрируют успешное догоняющее развитие, можно отнести Турцию, Иран, Египет и Индию, тогда как Россия, страны Латинской Америки и Африки южнее Сахары будут отставать [35]. В другой работе предложено уравнение экономического роста, увязывающее в явном виде темпы прироста ВВП с рентабельностью капитала (нормой прибыли) [36]. Проведенные авторами экспериментальные расчеты показали, что для получения положительных темпов роста необходимо наличие в экономике особого сектора, обладающего чрезвычайно высокой прибыльностью, исчисляемой сотнями и тысячами процентов. Данное положение получило название теоремы об особом секторе, где под особым понимается сектор экономики с рентабельностью, превышающей 100% годовых. Впоследствии данный тезис был эмпирически подтвержден большим числом стилизованных примеров из истории Нового времени [37]. Таким образом, можно говорить о традиции построения моделей экономического роста, которые одновременно позволяли бы раскрыть механизм и условия возникновения самого роста. Этот принцип будет использоваться в дальнейших построениях.

Экономический рост и рентабельность капитала. Гетерогенность национальной экономики подвергалась изучению с разных сторон. В частности, этой цели служит огромное разнообразие диффузионных моделей, призванных описать создание и распространение инноваций. Сегодня принято различать два типа участников инновационного рынка: фирмы–инноваторы (лидеры, создающие инновации) и фирмы–имитаторы (те, кто заимствует уже появившуюся на рынке инновацию). Однако ограниченность диффузионных моделей связана с эмпирическим фактом, согласно которому в экономике и в отдельных отраслях сосуществуют разноэффективные технологии, причем полного перетекания в сторону самых новых технологий не происходит. Для объяснения этого факта в 1988 г. была предложена модель Полтеровича–Хенкина [38], которая впоследствии не только обобщалась [39; 40] и модифировалась [41], но и использовалась для прикладных расчетов на основе данных о рентабельности предприятий черной металлургии СССР за 1976–1988 гг. [42]. Модель Полтеровича–Хенкина явилась знаковым достижением, ибо с ее помощью оказалось возможным в рамках одного относительно простого уравнения совместить процесс экономического роста и технологический прогресс с учетом фактора неодинаковой рентабельности разных групп предприятий.

На новый уровень проблема связи экономического роста и рентабельности капитала была поднята в научном бестселлере Т. Пикетти [2], в котором было предложено следующее неравенство: g<r, где g – темп экономического роста, а r – норма прибыли (рентабельность капитала). Пикетти называет это неравенство третьим законом капитализма, который означает, что рекапитализация капитала (имущества), накопленного в прошлом, протекает быстрее, чем растет производство, что, в конечном счете, ведет к углублению социального неравенства во всех своих проявлениях. Благодаря такой интерпретации эффект Пикетти превращается, по образному выражению Д. Макклоски, в «главное неравенство о неравенстве» [43], которое в научной литературе подверглось активному обсуждению (обзор критики Пикетти см. в [44]). В частности, Дж. Гелбрейт высказывал мнение, что закон Пикетти исчезнет так же быстро, как и появился [45]; более того, он пытался «уточнить» неравенство Пикетти следующим образом: g<r(1–u)–h, где u – налог на доходы с капитала; h – доля дохода капиталиста, отчисляемого на благотворительные цели. Однако более поздние построения позволили получить простую модель, в которой темпы экономического роста в явном виде связаны с рентабельностью капитала и не нарушают общую макроэкономическую логику; помимо этого, из построенной модели неравенство Пикетти вытекает как некое очевидное следствие, что доказывает его справедливость [36; 44]. Относительно наблюдения Пикетти о том, что на протяжении всей мировой истории до 1700 года доходность капитала была в 10–20 раз выше темпов роста производства [2], то экспериментальные расчеты показали его справедливость, а опасения о чрезмерности подобного разрыва в экономических величинах преувеличенными [44; 46].

Таким образом, можно констатировать традицию увязывания в модельных построениях темпов экономического роста с рентабельностью капитала, которая будет продолжена в дальнейших выкладках.

Рассмотренные выше 4 аспекта моделирования экономического роста задают ту систему координат, которая позволяет осуществлять аналитические построения в рамках сложившихся традиций, не приходя с ними в противоречия.

3. Фундаментальное уравнение накопления капитала. Для получения простого уравнения, связывающего темпы экономического роста и рентабельность капитала, воспользуемся для начала балансовым тождеством накопления основного капитала:

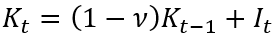                                                           (1)

где t – период времени (год); K_t и K_t–1 – объем основного капитала в национальной экономике в году t и t–1 соответственно; I_t – объем инвестиций в основной капитал в году t; ν – коэффициент выбытия основного капитала (предполагается постоянным).

Теперь воспользуемся традиционным предположением, что годовой объем инвестиций I определяется средней склонностью к накоплению (инвестированию) s (предполагается постоянной) и полученным доходом Y. Под последним предполагаем традиционный агрегат ВВП, который в соответствии с системой национальных счетов может определяться по источникам доходов и состоит из валовой прибыли π, затрат на заработную плату W и чистых налогов на продукты и импорт T. Тогда можно записать следующее уравнение:

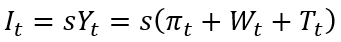                                           (2)

Для удобства предположим, что структура ВВП стабильна во времени. Тогда, введя структурные коэффициенты β=W_t/π_t и γ=T_t/π_t, уравнение (2) перепишем в следующем виде:

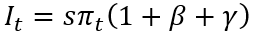                                                            (3)

Теперь подставим формулу (3) в (1) и разделим получившееся выражение на K_t–1. Если ввести обозначения для темпа накопления основного капитала λ=K_t/K_t–1–1 и нормы прибыли на капитал r=π_t/K_t–1, а также предположить неизменность данных двух переменные во времени, то в итоге получим выражение, которое в дальнейшем будем называть фундаментальным уравнением накопления капитала (ФУНК):

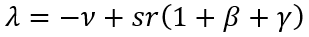                                                  (4)

Насколько нам известно, ранее в таком виде динамика капитала не описывалась.

Значение ФУНК состоит в явном совмещении скорости накопления основного капитала с его прибыльностью и склонностью к инвестированию. Именно такая форма уравнения (4) позволяет его использовать в дальнейшем при моделировании экономического роста.

4. Фундаментальное уравнение экономического роста. Следующим шагом к моделированию экономического роста является рассмотрение однофакторной производственной функции:

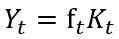                                                                                       (5)

где f_t – капиталоотдача, т.е. эффективность производства основного капитала.

На первый взгляд, функция (5) кажется несколько ограниченной в силу своей однофакторности, однако если использовать тождество f=P/k, где P=Y/L и k=K/L, L – численность занятых в экономике, P – средняя производительность труда, k – капиталовооруженность труда, то в описании (5) будет автоматически учитываться и эффективность труда (P), и технологическая оснащенность рабочего места (k):

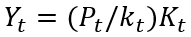                                                                         (6)

которое в динамической форме с учетом ФУНК можно представить следующим образом:

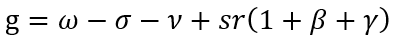                                (7)

где g, ω и σ – темпы прироста выпуска, производительности труда и капиталовооруженности соответственно.

В дальнейшем соотношение (7) будем называть фундаментальным уравнением экономического роста (ФУЭР), значение которого состоит в явной увязке темпа экономического роста (g), рентабельности капитала (r), инвестиционной активности (s) и параметров технологического прогресса (ω и σ), что и являлось нашей конечной целью. Заметим, что построенная модель (7) предполагает первичность процесса накопления капитала, а экономический рост – его следствием. Иными словами, исходным феноменом является круговорот капитала, который при определенных условиях может порождать режим экономического роста.

Отметим, что похожие выкладки были выполнены в более ранних работах [36; 44], однако в них рассматривались менее удачные формы учета полученного дохода и нормы прибыли, а также не учитывался технологический прогресс в производственной сфере.

Несложно видеть, что из уравнения (7) в качестве частного случая следует неравенство Пикетти g<r, однако его выполнение предполагает выполнение определенных условий и не является автоматическим и совсем тривиальным. Вместе с тем следует признать, что при реалистичных значениях макроэкономических параметров в ФУЭР неравенство Пикетти почти всегда выполняется.

5. Условие выхода из мальтузианской ловушки. Хотя из ФУЭР (7) можно получить неравенство Пикетти, оно представляет собой лишь побочный результат анализа. Более важным является определение условий, при которых обеспечиваются положительные темпы экономического роста на начальных этапах капитализма. Мальтузианская ловушка, строго говоря, имеет место при условии q=0, где q – темп прироста душевого уровня ВВП Q=Y/N, N – численность населения. Если ввести в рассмотрение темп прироста населения n, то справедливо равенство:

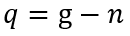                                                                                     (8)

Этого достаточно для исследования условий, обеспечивающих выход из мальтузианской ловушки, когда q>0. Для этого воспользуемся рядом упрощающих предположений, отражающих специфику периода между двух эпох – Средневековья и Нового времени. Будем полагать, что технологический прогресс в этот период еще отсутствовал в качестве системного явления, т.е. ω=σ=0. Другое допущение связано с отсутствием роста населения, т.е. n=0. Третий постулат основан на отсутствии рынка рабочей силы, следовательно, и феномена заработной платы, т.е. W→0 и β=0. Действительно, феодальное хозяйство предполагало, что каждый его участник выступал в качестве предпринимателя и жил не на заработную плату, а на доход со своего предприятия. Это не значит, что при феодальном строе заработная плата вообще отсутствовала, однако ее существование было крайне локальным и ограниченным. Для примера рассмотрим сословие моряков, которые получали определенное жалованье, однако само мореходство часто перерождалось, например, в пиратский промысел, который представлял собой форму коллективного предпринимательства и предполагал долю каждого участника в общей сумме добычи – дохода от бизнес–кампании. На данном примере хорошо видно, что в Средневековье заработная плата в основном принимала форму чистого дохода ремесленника или крестьянина. Таким образом, условие выхода из мальтузианской ловушки принимает предельно простой вид: r>ν/s(1+γ). Иными словами, экономический рост предполагает некий минимальный уровень рентабельности капитала.

Для понимания степени жесткости полученного ограничения осуществим элементарную оценку входящих в него параметров. Например, для экономики России 2008–2018 гг. средняя норма выбытия основного капитала составляла 10,5% [46, с. 78]; вряд ли в феодальную эпоху этот показатель сильно отличался в ту или иную сторону [2]. По имеющимся сведениям, норма накопления в Англии до 1760 г. не превышала 6% [35, с.46]. Относительно параметра γ можно строить разные гипотезы, однако, учитывая, что его значение для России за период 2011–2019 гг. составляло 30%, а в Средневековье помимо церковной десятины действовало множество акцизов и таможенных пошлин, то вполне правомерно исходить из величины γ=50–70% [3]. Тогда, как показывают расчеты, рентабельность капитала должна превышать 116,7 и 102,9% соответственно. Вполне резонно предположить, что для позднефеодальной экономики, в которой уже активно осуществлялись товарно–денежные операции, столь большая средняя отдача от капитала является нереальной. Единственный способ устранить противоречие между теоретическими и фактическими цифрами состоит в рассмотрении двух секторов экономики: обычного – с нормой прибыли r**≈5%, являющейся типичной для истории человечества с 1700 г. [2], и особого – с нормой прибыли, намного превышающей r*>100% годовых [37]; соответственно доля основного капитала в особом секторе невелика и составляет ζ=K*/K, тогда как обычный сектор занимает всю остальную часть экономики – 1–ζ: r=ζr*+r**(1–ζ); r*=π*_t/K*_t-1; r**=π**_t/K**_t-1; K=K*+K**, где K* и K** – объем основного капитала в особом и обычном секторах соответственно. В этом случае ФУНК принимает вид:

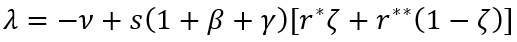       (9)

Тогда обобщение ФУЭР будет выглядеть следующим образом:

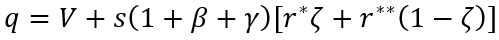           (10)

где используется обозначение V=ω–σ–ν–n.

Утверждение о необходимости существования особого (сверхрентабельного) сектора экономики для перехода из мальтузианского режима развития к экономическому росту и составляет содержание теоремы об особом секторе [36]. Как уже отмечалось, более пристальное рассмотрение истории Нового времени показало, что такой сектор действительно существовал [37].

Указанное обстоятельство имеет огромное значение.

Во-первых, оно недвусмысленно говорит о том, что переход к режиму экономического роста требовал в качестве необходимого условия наличие возможности получения сверхприбылей. Это требование является крайне жестким, но благодаря уникальному стечению обстоятельств – эпохе великих географических открытий, жестокой колонизации европейцами Нового и Старого света, серии важных технологических инноваций и т.п. – оно оказалось выполненным. Однако, судя по всему, достаточным условием окончательного разрушения мальтузианской ловушки явились личностные качества европейцев, которые В. Зомбартом были объединены в дух предпринимательства. Сюда относятся разные человеческие качества – изобретательность, религиозное рвение, гибкая логика, жажда наживы, агрессивность и жестокость, умение считать и копить и т.д. [47, с.125]. Объективная возможность и субъективное стремление обогащаться совпали для европейских народов на рубеже эпох. Одно без другого многократно имело место в истории, но не дало никаких плодов. Не давая оценки данному обстоятельству, укажем лишь на неизмеримые социальные жертвы, которые потребовались Европе для построения капитализма [48].

Во-вторых, ФУЭР (10) демонстрирует, что в истории экономического роста имеют место две принципиально различные фазы – начальная, когда осуществляется первоначальное накопление капитала и только запускается спираль роста, и зрелая, когда все макроэкономические процессы достигли своего нормального значения. Чтобы продемонстрировать, насколько жесткие требования предъявляет ФУЭР к величине нормы прибыли в разных фазах роста, проведем простейшие расчеты. Так, компонент s(1+β+γ) в начальной фазе (s=6%, β=0, γ=50%) составляет величину 0,09, тогда как в зрелой фазе (s=45%, β=1,12, γ=0,30) – 1,089. Тем самым данный компонент при переходе от первой фазы ко второй увеличивается в 12 раз, что свидетельствует о кардинальном изменении всего макроэкономического климата и требует уже среднюю рентабельность капитала национальной экономики не в 116,7%, а всего лишь в 9,6%. Таким образом, именно переходный период к режиму роста представляет собой масштабную историческую проблему, в то время как поддержание стационарного роста уже не требует слишком жестких усилий. Если же учесть, что в зрелой фазе роста «включается» технологический прогресс (ω>0), то требования по сохранению национальной экономики на экспоненциальной траектории оказываются еще более щадящими.

При обсуждении ФУЭР (10) необходимо отметить следующее. Строго говоря, данная модель отражает потенциальный рост экономики, т.к. в ней не учтен спрос на выпускаемую продукцию, который может снизить расчетные цифры. Тем не менее, для понимания основных движущих сил экономического роста уравнения (10) вполне достаточно. При этом особо подчеркнем следующее обстоятельство: на начальных этапах установления режима роста производства все аномально низкие макроэкономические параметры компенсируются величиной рентабельности капитала, что и является основанием теоремы об особом секторе экономики. По мере роста других макропараметров «нагрузка» на норму прибыли постепенно падает и в национальной экономике устанавливаются более естественные пропорции, позволяющие поддерживать стационарный рост в течение длительного времени без внутреннего напряжения, характерного для начальной фазы.

6. Преодоление мальтузианской ловушки: технологический эффект масштаба и рост населения. ФУЭР (10) сконструировано таким образом, что демографический рост и рост производительности труда выступают в качестве экзогенных факторов. Чтобы хотя бы в самом общем виде отразить существующие обратные связи в социальной системе, введем два простых предположения, а именно: рост населения нелинейно зависит от уровня его благосостояния (душевого уровня ВВП), а производительность труда нелинейно зависит от уровня капиталовооруженности производства. Тогда справедливы следующие соотношения:

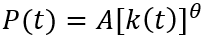                                                                     (11)

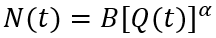                                                                   (12)

где Q=Y/N; A, B, α и θ – параметры–константы.

Из (11) и (12) вытекает, что ω=(θ–1)σ и n=αq, а ФУЭК (10) конкретизируется следующим образом:

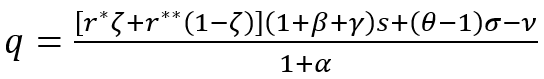   (13)

Из формулы (13) вытекает два важных вывода. Первый достаточно очевидный и состоит в том, что рост населения по мере роста производства (т.е. α>0) сам по себе не влияет на экономический рост, но препятствует выходу их мальтузианской ловушки; ускоренный же рост населения (т.е. α>1) очень сильно (более чем в 2 раза) тормозит увеличение душевого дохода. Второй вывод является менее очевидным и означает зависимость динамики производства от «зрелости» технологического прогресса: если имеет место технологический эффект масштаба (т.е. θ>1), то технологический прогресс оказывает стимулирующее влияние на экономический рост; в противном случае он выступает в качестве фактора торможения. Последнее утверждение кажется парадоксальным, однако в реальности его интерпретация достаточно проста: поток основного капитала стимулирует экономический рост при условии, что скорость удорожания рабочего места не должна быть больше скорости роста производительности труда (ω>σ). Нарушение этого условия означает неэффективность вложений в основной капитал или, если быть точнее, затраты на совершенствование рабочего места не окупаются масштабом экономии затрат на рабочую силу; прикладные расчеты показали, что сегодня отнюдь не во всех странах действует технологический эффект масштаба (θ>1) [24].

Сказанное предполагает, что на стадии преодоления мальтузианской ловушки внедряемые технологические инновации должны приводить к массовому вытеснению производственных работников, как, например, при внедрении разных модификаций ткацкого станка. При этом желательно, чтобы в этот момент отсутствовало демографическое давление, для чего необходимо осуществить «разгрузку» рынка труда, что в европейских странах достигалось довольно жесткими законами и действиями властей (подробнее об этом см. в [48]).

Таким образом, теоретические построения показывают, что выход из мальтузианской ловушки предполагал крайне жесткие меры нарождающегося слоя буржуа против народных масс и высокую норму эксплуатации человека человеком. Именно такое положение дел обеспечивало сверхвысокую рентабельность экономических операций и позволяло поддерживать интенсивность накопления капитала, достаточную для запуска экономического роста.

Важным элементом построенной модели является ее монокаузальный характер. Например, имеется большой массив работ, в которых процесс перехода от депрессии к росту объясняется генерацией и распространением производственных технологий, а также ростом человеческого капитала в процессе данной деятельности [49] [4]. Стала популярной и идея учета распределения богатства среди групп населения и возникающего вследствие этого политического конфликта [50; 51]. При этом практически во всех моделях импульс к изменению режима развития исходит из наличия множества (или хотя бы двух) гетерогенных секторов экономики или социальных групп, которые различаются по множеству параметров (богатство, объем человеческого капитала, экономическая эффективность и т.п.). Согласно такому представлению гетерогенность сегментов экономики инициирует масштабную диффузию ресурсов в направлении более эффективных элементов системы. В отличие от такого подхода ФУЭР для переходного процесса как бы схлопывает все различия между структурными элементами в один интегральный показатель – рентабельность капитала. Что же касается фактора гетерогенности экономики, то он учитывается в ФУЭР максимально просто – путем введения двух секторов разной прибыльности, а взаимодействия между ними в явной форме не предполагается.

7. Результаты модельных расчетов. Чтобы проверить чувствительность национальной экономики к разным параметрам и, прежде сего, к рентабельности особого сектора, рассмотрим 10 сценариев на основе экспериментальных расчетов по формуле (13), в которой балансирующей переменной выступает r*. При этом четыре параметра будем считать неизменными: γ=30,0%; ν=10,5%; q=2,0%; r**=5,0%. Остальные параметры меняются в направлениях, позволяющих определить масштаб исследуемого явления (табл. 1).

Сценарий №1 фиксирует самый неблагоприятный вариант развития, когда отсутствует технологический прогресс и сектор наемного труда, но имеется демографическое давление, ничтожная инвестиционная активность и очень ограниченный размер особого сектора. Как видно из табл. 1, в этом случае рентабельность капитала в особом секторе должна достигать 4–значных цифр в процентном исчислении. Из сценария №2 видно, что снятие демографического давления само по себе не может принципиально изменить требования к прибыльности особого сектора, однако рост его относительного размера понижает нижний порог до 3–значных значений. По-видимому, сценарии №4 и №5 наилучшим образом соответствуют ситуации, в которой находилась английская экономика накануне процесса всеобщей капитализации. Как показывают расчеты, существование довольно солидного сектора экономики с рентабельностью в сотни процентов является главным требованием к преодолению мальтузианской ловушки в начальной фазе капиталистического строя. Напомним, что под особым сектором понимается сегмент экономики с рентабельностью выше 100% годовых; имеющиеся исторические факты убедительно показывают возникновение в Новое время большого числа видов бизнеса с фантастической нормой прибыли [37].

Таблица 1. Результаты экспериментальных расчетов по модели (13).

Сценарии №6–8 демонстрируют, что в зрелой фазе капитализма, для которой характерен существенный рост нормы накопления, требование к прибыльности особого сектора существенно уменьшается вплоть до потери самого смысла особого сектора, когда его рентабельность падает до 2–значных значений. Если же к умеренно высокой инвестиционной активности добавить развитый сектор наемного труда и скромный технологический прогресс, то, как показывают сценарии №9–10, даже рост населения оставляет требование к прибыльности небольшой части экономики на вполне реалистичном уровне. Несмотря на это, сегодня по-прежнему имеется достаточно обширный рыночный сегмент, в котором рентабельность производства достигает 3–значных цифр [37]. В целом же на стадии зрелой фазы капитализма нижний порог рентабельности экономики снижается примерно на порядок по сравнению с начальной фазой.

8. Модель роста для многосекторной экономики. Выведенное ФУЭР (10) имеет большое значение, т.к. показывает, что гетерогенность национальной экономики сама по себе может выступать в качестве фактора экономического роста. Однако в уравнении (10) для простоты рассматривалось только два сектора – низко– и высокорентабельный. На самом деле в реальной экономике ее секторы (отрасли, предприятия и т.п.) образуют определенную иерархическую последовательность в зависимости от уровня их эффективности. Более того, как показано в [38; 39], установившееся распределение сохраняется в течение неопределенно долгого времени. В связи с этим уравнение (10) предполагает очевидное обобщение, которое в дискретной форме выглядит следующим образом:

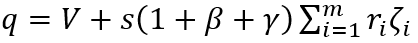                           (14)

где r_i – рентабельность капитала i–го сектора экономики; ζ_i – доля основного капитала в i–ом секторе экономики; m – число секторов в национальной экономике.

В непрерывной форме уравнение (14) будет выглядеть аналогично:

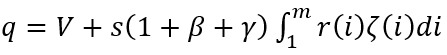                     (15)

где используются аналогичные обозначения.

В такой форме ФУЭР позволяет увязать неравномерность развития экономики с темпом экономического роста. Более того, нижний порог рентабельности экономики, обеспечивающий положительные темпы роста ВВП, и нижний порог низкорентабельных производств автоматически задают нижний уровень неравномерности развития отдельных секторов. Главное же достоинство уравнений (14) и (15) состоит в том, что они позволяют представить национальную экономику в виде многоуровневой системы, в которой каждый уровень представлен своими характеристиками эффективности и масштаба.

9. Драйвер экономического роста на ранних стадиях развития общества. Согласно ФУЭР в форме (14) и (15) национальная экономика представляет собой иерархическую систему, что позволяет по-новому посмотреть на источники экономического роста. В частности, становление капитализма привело к закреплению в качестве главного мерила и критерия успешности любой экономической деятельности отдачу (рентабельность) капитала или, что то же самое, норму прибыли (процент). Однако процент в разных формах существовал и задолго до капитализма, но не способствовал запуску экономического роста. Данный факт нуждается в системном объяснении, которое может быть дано в терминах уравнения (14).

Так, из уравнения (7) следует общее положение: только достаточно большая средняя норма прибыли способна обеспечить положительные темпы экономического роста. Лишь при переходе количества в качество данный параметр начинает играть роль драйвера тотального роста производства. Однако достаточно высокий доход с капитала не только обеспечивает поток инвестиций, необходимый для поддержания экономического роста, но и выступает в качестве стимула для больших масс людей, чтобы браться за рискованные виды деятельности. Этот момент является ключевым для психологии предпринимателя: нужна не просто прибыль, а сверхприбыль для того, чтобы породить неугасаемый интерес у больших групп населения к бизнесу и заставить их перейти к активной деятельности, несмотря на возможные угрозы и препятствия.

Именно сверхприбыль рождает жажду наживы, которая в свою очередь выступает драйвером бизнес–активности. Вряд ли, состоялись бы завоевания конкистадоров, если бы на кону стоял доход с капитала в 10–15% годовых. Только баснословный по нынешним меркам процент с капитала мог разжечь в людях дух предпринимательства. Однако уточняющее положение, вытекающее из уравнения (14), состоит в том, что сказочное обогащение возможно только в некоторых видах бизнеса, тогда как другие отрасли вынуждены довольствоваться гораздо более скромными доходами. Например, торговля пряностями с нормой прибыли в 600–700% годовых стимулирует кораблестроение, которое в свою очередь требует строительства портов и складских помещений и т.д. Иными словами, от самой доходной деятельности бизнес–импульсы расходятся по всем остальным секторам экономики, вплоть до рутинных и нерентабельных производств. Таким образом, при наличии иерархии секторов экономики по уровню прибыльности возникает своеобразный эффект мультипликатора, благодаря которому бизнес-активность распространяется по всей экономике сверху вниз – от сверхрентабельных видов деятельности до бесприбыльных предприятий.

Еще раз подчеркнем, что в феодальной экономике даже ростовщики и спекулянты городскими облигациями могли рассчитывать в лучшем случае на десятки процентов прибыльности своих вложений, тогда как эпоха великих географических открытий, совместившаяся с ранней индустриализацией, позволила появиться таким видам производства и торговли, рентабельность которых достигала сотен и тысяч процентов [37]. Не менее важным является и то, что феномен сверхприбыльности бизнеса в ранней капиталистической экономике имел массовое распространение. Именно стремление больших групп людей к быстрому обогащению и выступило в качестве драйвера экономического роста. В дальнейшем борьба за сохранение монополии на сверхприбыльные ниши экономики послужила непосредственной причиной многочисленных жестокостей и злоупотреблений европейцев по отношению друг к другу и другим народам. Как показал Дж. Арриги, с этого момента контроль нормы прибыли стал главной задачей системы капиталистического управления [52].

10. Заключение. История показывает, что феномен экономического роста, капиталистический строй, устойчивый технологический прогресс и цивилизованный институт частной собственности, включая интеллектуальную собственность, возникли одновременно. Это позволяет предположить, что распад указанной системы из четырех составляющих будет также происходить одновременно и будет означать конец капитализма как такового. Полученное в предыдущих разделах ФУЭР содержит в себе параметры всех названных явлений и тем самым отражает сущностные аспекты роста экономики. Кроме того, из уравнения (7) не только следует неравенство Пикетти, но и строгие условия его выполнения.

Сказанное, помимо всего прочего, позволяет подойти к конструктивному обсуждению завершающей фазы капитализма. Например, имеющееся перенакопление капитала и уменьшение его доходности вплоть до введения банковской системой многих стран отрицательного процента является большой проблемой для поддержания экономического роста. Подобного обесценения капитала раньше не было. Кроме того, в США и странах Европы вводятся законы, разрешающие бездомным людям занимать чужое пустующее жилье. Такого отрицания основополагающего права частной собственности также ранее никогда не наблюдалось. Если же предположить, что опасения Пикетти в отношении грядущего обнуления доходности капитала верны, то согласно уравнению (7) рост экономики может быть обеспечен только за счет очень интенсивного повышения производительности труда и увеличения срока службы производственного оборудования. Подобное развитие событий фактически означает стремительную роботизацию производства, которая, судя по всему, представляет собой завершающую фазу капитализма. Не следует сбрасывать со счета и то обстоятельство, что экономический рост уже практически достиг своего физического предела, когда его сохранение чревато полным разрушением среды обитания человека. Если же учесть, что главенство капитала, экономический рост, технологический прогресс и право собственности переплетены между собой и друг без друга не существуют, то можно говорить о наметившихся признаках конца капиталистического строя.

Вряд ли капитализм уже полностью исчерпал себя и человечество готово к совершенно иной социальной модели бытия, однако если это действительно произойдет, то остается лишь гадать, что станет новым драйвером дальнейшего экономического развития.

Литература

1. Норт Д. Понимание процесса экономических изменений. М.: Изд. дом ГУ–ВШЭ, 2010. 256 с.

2. Пикетти Т. Капитал в XXI веке. М.: Ад Маргинем Пресс, 2016. 592 с.

3. Heinberg R. The End of Growth: Adapting to Our New Economic Reality. Cabriola Island, B.C.: New Society Publishers, 2011. 321 p.

4. Solow R.M. A contribution to the theory of economic growth // The Quarterly Journal of Economics, 1956. Vol. 70, no. 1, pp. 65–94.

5. Uzawa H. On a two-sector model of economic growth // Readings in the Theory of Growth, 1971, p. 19–26.

6. Romer P. Are nonconvexities important for understanding growth? / National Bureau of Economic Research, 1990, №w3271 (https://www.nber.org/papers/w3271.pdf – Дата обращения: 12.02.2020).

7. Malawi A.I., AlMansi M. Economic Globalization and Labor Productivity: An Application of Autoregressive Distributed Lag (ARDL) Bounds Testing Approach // International Journal of Business and Statistical Analysis, 2014, no. 1, p. 49–55.

8. Knoblach M., Stöckl F. What determines the elasticity of substitution between capital and labor? A literature review / DIW Berlin Discussion Paper, 2019. No. 1784 (https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3339171 – Дата обращения: 12.02.2020).

9. Klump R., de La Grandville O. Economic growth and the elasticity of substitution: Two theorems and some suggestions // American Economic Review, 2000, No. 90(1), p. 282–291.

10. Caselli F. Accounting for Cross–Country Income Differences / In Durlauf, P. A. and Steven, N., (Eds) Handbook of Economic Growth, 2005, v. 1, Part A, Elsevier, p. 679–741.

11. Acemoglu D. Labor– and capital–augmenting technical change // Journal of the European Economic Association, 2003, V. 1, p. 1–37.

12. Mankiw N.G., Phelps E.S., Romer P.M. The growth of nations // Brookings papers on economic activity, 1995, V. 1, p. 275–326.

13. Wolff E.N. Capital formation and productivity convergence over the long term // The American Economic Review, 1991, V. 81, No. 3, p. 565–579.

14. Solow R.M. Technical Change and the Aggregate Production Function // The Review of Economics and Statistics, 1957, No. 39(3), p. 312–320.

15. Kurz M. The General Instability of a Class of Competitive Growth Process // Review of Economic Studies, 1968, No. 35, p. 155–174.

16. Goldman S.M. Optimal Growth and Continual Planning Revision // Review of Economic Studies, 1968, No. 35, p. 45–54.

17. Hahn F. On Warranted Growth Paths // Review of Economic Studies, 1968, No. 35, p. 175–184.

18. Broadberry S.N., Irwin D.A. Labor productivity in the United States and the United Kingdom during the nineteenth century // Explorations in Economic History, 2006, No. 43(2), p. 257–279.

19. Jefferson G.H., Rawski T.G., Zhang Y. Productivity growth and convergence across China's industrial economy // Journal of Chinese Economic and Business Studies, 2008, No. 6(2), p. 121–140.

20. Dollar D. Economic reform and allocative efficiency in China's state–owned industry // Economic Development and Cultural Change, 1990, No. 39(1), p. 89–105.

21. Ezzahid E., Nihou A. Capital deepening and efficiency in Morocco / MPRA Paper, 2017, No. 82143 (https://pdfs.semanticscholar.org/7ce8/a96a40a5c6449ce9e54ea94f28175e105698.pdf – Дата обращения: 12.02.2020).

22. Aghion Ph., Howitt P. A Model of Growth Through Creative Destruction // Econometrica, 1992, vol. 60, no. 2, pp. 323–351.

23. Aghion Ph., Howitt P. Capital Accumulation and Innovation as Complementary Factors in Long-Run Growth // Journal of Economic Growth, 1998, no. 3, pp. 111–130.

24. Балацкий Е.В., Юревич М.А. Технологический эффект масштаба и экономический рост // Terra Economicus, Том 18, №1, 2020. С. 43–57.

25. Lee R. A Historical Perspective on Economic Aspects of the Population Explosion: The Case of Preindustrial England // Population and Economic Change in Developing Countries / Ed. by R.A.Easterlin, pp. 517–566. Chicago, IL: University of Chicago Press, 1980.

26. Wood J.W. A Theory of Preindustrial Population Dynamics, Demography, Economy, and Well-Being in Malthusian Systems // Current Anthropology, 1998, No. 39, pp. 99–135.

27. Voigtlander N., Voth H. Malthusian Dynamism and the Rise of Europe: Make War, Not Love // American Economic Review: Papers & Proceedings, 2009, No. 99(2), pp. 248–254.

28. Ashraf Q., Galor O. Dynamics and Stagnation in the Malthusian Epoch // American Economic Review, 2011, No. 101(5), pp. 2003–2041.

29. Møller N., Sharp P. Malthus in Cointegration Space: A New Look at Living Standards and Population in Pre–Industrial England // Journal of Economic Growth, 2014, Vol.19, No.1, pp. 105–140.

30. Artzrouni M., Komlos J. Population Growth through History and the Escape from the Malthusian Trap: A Homeostatic Simulation Model // Genus, 1985, vol. 41, no. 3–4, pp. 21–39.

31. Steinmann G., Prskawetz A., Feichtinger G. A Model on the Escape from the Malthusian Trap // Journal of Population Economics, 1998, no. 11, pp. 535–550.

32. Kogel T., Prskawetz A. Agricultural Productivity Growth and Escape from the Malthusian Trap // Journal of Economic Growth, 2001, vol. 6, no. 4, pp. 337–357.

33. Коротаев А.В., Малков А.С., Халтурина Д.А. Законы истории: Математическое моделирование развития Мир–Системы. Демография, экономика, культура. М.: Ленанд. 2019. 230 с.

34. Гринин Л.Е., Коротаева А.В., Малков С.Ю. Математические модели социально–демографических циклов и выхода из «мальтузианской ловушки»: некоторые возможные направления дальнейшего развития / В сб.: Проблемы математической истории: Математическое моделирование исторических процессов / Ред. Г.Г. Малинецкий, А.В. Коротаев. М.: URSS. 2008. С. 78–118.

35. Попов В.В. Почему Запад разбогател раньше, чем другие страны, и почему Китай сегодня догоняет Запад? Новый ответ на старый вопрос // Журнал Новой экономической ассоциации, 2012. №3(15). С.35–64.

36. Балацкий Е.В., Екимова Н.А. Внешнеторговый фактор в ликвидации мальтузианской ловушки / В сб.: Экономическая теория и хозяйственная практика: глобальные вызовы. Материалы международной конференции «Эволюция международной торговой системы: проблемы и перспективы – 2016». СПб.: Санкт-Петербургский государственный университет, 2016. C. 165–172.

37. Балацкий Е.В., Екимова Н.А. «Особый сектор» экономики как драйвер экономического роста // Journal of New Economy, Т. 21, № 3, 2020. С. 5–27.

38. Полтерович В.М., Хенкин Г.М. Эволюционная модель взаимодействия процессов создания и заимствования технологий // Экономика и математические методы, №6, 1988. С. 1071–1083.

39. Полтерович В.М., Хенкин Г.М. Эволюционная модель экономического роста // Экономика и математические методы, №3, 1989. С. 518–531.

40. Henkin G.M., Polterovich V.M. A difference–differential analogue of Burgers equation and some models of economic development // Working Paper #WP/98/051, Moscow, CEMI of Russian Academy of Science, 1998. 61 p.

41. Ташлицкая Я.М., Шананин А.А. Моделирование процесса распространения технологий. М.: Вычислительный центр РАН, 2000. 50 с.

42. Гельман Л.М., Левин М.И., Полтерович В.М., Спивак В.А. Моделирование динамики распределения предприятий отрасли по уровням эффективности (на примере черной металлургии) // Экономика и математические методы, №3, Том 29, 1993. С. 460–469.

43. Макклоски Д.Н. Измеренный, безмерный, преувеличенный и безосновательный пессимизм. О книге «Капитализм в XXI веке» Томаса Пикетти // Экономическая политика, 2016. Т.11, № 4, 2016. С. 153–195.

44. Балацкий Е.В. Эффект Пикетти: комментарий к новой концепции // Terra Economicus, Том 15, №2, 2017. С. 40–56.

45. Galbraith J.K. Unpacking the first fundamental law // Real–world Economics Review, 2014, no. 69, 7 October, pp. 145–148.

46. Балацкий Е.В. Институт социального неравенства и экономический рост // Журнал институциональных исследований, Том 12, №1, 2020. С. 66–83.

47. Зомбарт В. Буржуа: Этюды по истории духовного развития современного экономического человека. М.: ТЕРРА – Книжный клуб, 2009. 637 с.

48. Балацкий Е.В. Институциональная дилемма в период первоначального накопления капитала // Журнал экономической теории, №4, 2013. С.58–69.

49. Веселов Д.А. Провалы рынка и провалы государства в модели перехода от стагнации к развитию // Журнал Новой экономической ассоциации, 2011, № 12. С. 24–40.

50. Яркин А.М., Веселов Д.А. Распределение богатства и политический конфликт в модели перехода от стагнации к развитию // Журнал Новой экономической ассоциации, 2016. Т. 32. № 4. С. 30–60.

51. Veselov D.A. The dynamics of social conflict during the transition from stagnation to growth // Revue d'Economie Politique. 2019. Vol. 129. No. 5. P. 833–859.

52. Арриги Дж. Долгий двадцатый век: Деньги, власть и истоки нашего времени. М.: Издательский дом «Территория будущего», 2006. 472 с.