Введение
В экономической науке одним из магистральных направлений является проблема сопряжения социального неравенства и экономического роста, включая прямые и обратные связи между двумя явлениями. При этом ключевой вопрос – о том, как влияет социальное неравенство на экономический рост – решается преимущественно на основе построения эконометрических моделей. Вместе с тем эконометрика предполагает контекстный анализ, затрагивающий конкретные группы стран и временные периоды; выход за исходные территориальные и временные границы часто ведет к нарушению обнаруженных зависимостей. В связи с этим эконометрические построения не дают универсальных выводов. В свою очередь чисто аналитическое исследование указанной связи имеет свои недостатки и часто приводит к довольно сложным и непрозрачным моделям. Между тем некоторые принципиальные положения влияния института социального неравенства на экономический рост могут быть получены чисто аналитически и дать оценку масштабов указанного влияния. Цель данной статьи – найти аналитические выражения между темпами экономического роста и показателями доходного неравенства и оценить количественно возникающие эффекты.
Важный момент обозначенной проблемы состоит в дискуссионности тезиса, согласно которому институт неравенства не только стимулировал экономический рост в момент зарождения капитализма и способствовал выходу европейских стран из мальтузианской ловушки (МЛ), но и до сих пор выступает в качестве роста. Ниже мы сформулируем аргументы в пользу этого тезиса [1].
Обзор литературы
В литературе неоднократно обсуждался тезис о том, что рост социального неравенства явился одним из ключевых факторов преодоления ведущими странами мира проблемы МЛ (Попов, 2012). Однако этот тезис нуждается в более подробном обсуждении, которое началось с пионерных работ С. Кузнеца (Kuznets, 1955) и Н. Калдора (Kaldor, 1956), положивших начало изучению двусторонней связи между институтом неравенства и экономическим ростом. Вслед за этим начались объяснения параболической формы кривой Кузнеца, задающей зависимость между неравенством и уровнем душевого ВВП. Одно из наиболее прозрачных объяснений второй фазы кривой Кузнеца предложил М. Ахлувалия (Ahluwalia, 1976), однако в это же время Ш. Робинсон (Robinson, 1976) на основе простейших математических преобразований с дисперсиями доходов продемонстрировал возникновение перегиба кривой Кузнеца при минимальных экономических предпосылках. Подобные манипуляции по обоснованию кривой Кузнеца продолжили С. Ананд и С. Канбур (Anand, Kanbur, 1993). Последовавший за этим поток публикаций по данной теме отчасти подытожил Б. Гершман (Гершман, 2009а; Гершман, 2009б).
Однако поток работ по проблеме неравенства и роста не прекращается. Так, в статье (Behringer, van Treeck, 2019) авторы, возвращаясь к идеям М. Калецкого, строят так называемую неокалецкианскую модель, ориентированную на функциональное распределение доходов с дополнительным блоком потребления домашних хозяйств. Подобная модель позволила объяснить различия в развитии Германии, опирающейся на свои экспортные возможности, и США, использующие долговые инструменты. В работе (Clarke, 1992) отстаивается консервативный тезис о том, что неравенство не является необходимым условием экономического роста; наоборот, более медленный рост может возникать из-за конфликтов по поводу распределения доходов, что в свою очередь стимулирует более активное государственное вмешательство, заканчивающееся повышением налогов и стагнацией. В работе (Onaran, Galanis, 2014) роль неравенства исследуется посредством влияния доли заработной платы на экономический рост в странах G20. Как оказалось, сокращение указанной доли приводит к снижению темпов роста в Германии, Франции, Италии, Великобритании, США, Японии, Турции и Южной Корее, в то время как в Канаде, Австралии, Аргентине, Мексике, Китае, Индии и Южной Африке оно оказывает стимулирующее влияние. В статье (Tavani, Zamparelli, 2018) рассматривается модификация модели Гудвина, в которой правительство инвестирует в инфраструктуру и научные исследования и разработки, которые увеличивает темпы роста производительности труда. Авторы исследуют такой распределительный инструмент, как налоги, и показывают, что при условии превышения эластичности выпуска по инфраструктуре величины эластичности выпуска по производительности труда существует налоговая ставка, которая максимизирует объем рабочей силы и экономического роста; в целом же, различные схемы налогообложения могут по-разному влиять на стабильность циклов роста.
В статье (Sakaki, 2017) на основе имитационной модели показано, что в фазе активного экономического роста себя лучше чувствуют страны с более равномерным распределением доходов за счет стимулирования потребительского спроса и поддержания за счет этого производства; в фазе же замедления экономического роста гораздо лучше проявляют себя страны с высокой концентрацией доходов за счет продуцирования инвестиций и связанных с этим технологических изменений. Авторы (Berg, Ostry, 2017) утверждают, что неравенство и нестабильный рост – это две стороны одной медали, в частности, они приходят к выводу о том, что более длительный экономический рост прочно связан с большим равенством в распределении доходов. В статье (Dutt, 2017) рассматриваются неокейнсианские, неокалецкианские и неомарксистские теории для объяснения связи неравенства и роста, что подводит автора к довольно лапидарному выводу: литература по гетеродоксальным теориям роста обширна и продолжает активно расти, ибо ортодоксальные теории откровенно игнорируют множество важных факторов и вопросов. В статье (Milanovic, 2016) на основе эмпирических данных обследований домохозяйств более чем в 100 странах показано, что выгоды от доходов, которые богатые могут получить за счет их более неравномерного распределения, часто намного больше, чем выгоды от экономического роста, нейтрального к распределению. Данный факт позволил автору сделать вывод о том, что группа богатых людей с большей вероятностью будет поддерживать политику, направленную на увеличение неравенства, нежели беспокоиться об экономическом росте в своих странах. Надо сказать, что попытки включения в модели роста разных факторов и элементов превратились уже в своеобразную традицию. Например, в работе (Arestis, Baltar, 2017) в инвестиционную функцию вводится норма прибыли, что нарушает традиционные выводы о совмещении режимов экономического роста и распределения доходов. В этом же русле следуют авторы (Aoki, Nirei, 2016), которые строят модель с распределением доходов по Парето и показывают, что концентрация богатства увеличивается при высоких инвестиционных рисках и темпах экономического роста.
Из последних эконометрических работ наиболее продуктивной следует признать статью М. Юревича (Юревич, 2019), в которой была построена «обратная» функция Кузнеца, задающая зависимость темпов роста ВВП от величины индекса Джини. Получившаяся параболическая эконометрическая функция на данных 80 ведущих экономик мира продемонстрировала, что положительные темпы экономического роста возможны в интервале индекса Джини от 23,7 до 69,8; максимум кривой роста достигается при значении индекса Джини 46,7. Тем самым данные расчеты существенно скорректировали социально опасную верхнюю границу неравенства в сторону ее увеличения. В работе (Балацкий, 2013) была сделана попытка нащупать нижнюю границу доходного неравенства, за которой снижается инвестиционная активность. Ниже мы дадим более развернутый анализ данного аспекта проблемы соотношения неравенства и экономического роста.
Теорема об инвестиционном доминировании гетерогенного общества
Рассмотрим два типа общества – гомогенное и гетерогенное. Первое является бесклассовым и состоит из N равносостоятельных индивидов с доходом xM, который одновременно является среднедушевым; совокупный доход общества составляет X=NxM. Второе общество является 2–классовым, состоящим из NR богатых и NP бедных людей со средним доходом xR и xP соответственно. Общая численность населения
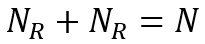 (1)
(1)
и сумма дохода в двух типах общества равны:
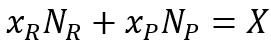 (2)
(2)
Таким образом, первое общество однородно по доходу и состоит из «середняков», тогда как второе состоит из двух групп субъектов, которых можно назвать условно богатыми и условно бедными в том смысле, что xR>xP. Схематично различия между гомогенным и гетерогенным обществами показано на рис. 1.
Будем предполагать, что каждое общество генерирует некое количество инвестиций в основной капитал – IHO и IHE – в соответствии со сложившейся в них нормой инвестирования:
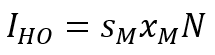 (3)
(3)
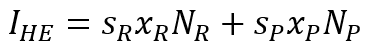 (4)
(4)
где sM, sR и sP – норма инвестирования (накопления) групп середняков, богатого и бедного населения соответственно; предполагается, что для разного уровня доходов характерна разная норма инвестированиия.
Соотношения (1)–(4) следует дополнить условием инвестиционного равновесия:
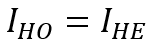 (5)
(5)
Основная аналитическая интрига состоит в том, какое общество – гомогенное или гетерогенное – генерирует больше инвестиционных ресурсов в экономику. Данная задача может быть сформулирована и в более общей постановке: определить условия, при которых гетерогенное общество порождает инвестиций больше, чем гомогенное. При реализации подобного режима можно говорить об инвестиционном доминировании гетерогенного общества.
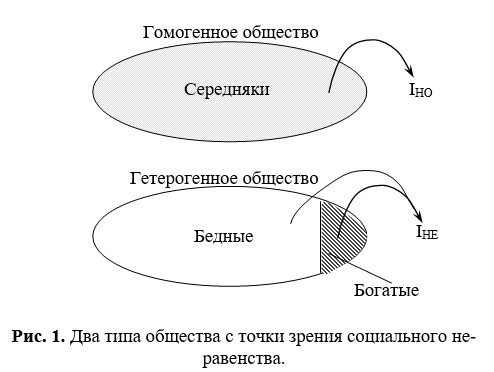
Если ввести в рассмотрение меру социального неравенства в виде разрыва в доходах бедных и богатых ς=xR/xP и долю бедного населения λ=NP/N, то можно сформулировать теорему об инвестиционном доминировании гетерогенного общества; для краткости будем ее назвать теоремой об инвестиционном доминировании (ТИД).
Теорема (об инвестиционном доминировании): При наличии двух типов общества – гомогенного и гетерогенного – в условиях слабого действия основного психологического закона накопления Кейнса и при достаточно высоком социальном (доходном) неравенстве ς>ς* гетерогенное общество генерирует больше инвестиций, чем гомогенное; пороговое значение социального неравенства задается соотношением:
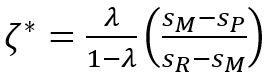 (6)
(6)
Доказательство. ТИР непосредственно следует из редуцирования соотношений (1)–(5) в окончательное выражение (5) с учетом введенных обозначений, откуда и выводится искомая формула (6). Если ς>ς*, то IHE>IHO; в противном случае гомогенное общество оказывается более эффективным в отношении инвестиционной активности: IHE<IHO.
Сначала докажем необходимость условия теоремы, что эквивалентно доказательству факта положительности значения ς* (т.е. ς*>0); в этом случае решение задачи не является вырожденным и имеет элементарный экономический смысл. Для этого нужно, чтобы выражение в круглых скобках в (6) было положительным, что гарантируется положительностью разницы норм накопления в рассматриваемых парах. Последнее требование может быть обосновано посредством обращения к так называемому основному психологическому закону накопления (потребления) (ОПЗН), сформулированному Дж.М. Кейнсом. Согласно его первоначальной формулировке, «…с ростом реального дохода, как правило, более высоким оказывается удельный вес той части дохода, которая направляется в сбережения. Будет ли, однако, эта доля больше или меньше, мы все равно можем видеть основной психологический закон, присущий любому современному обществу, в том, что с ростом реального дохода оно не увеличит своего потребления на всю абсолютную сумму прироста и, следовательно, будет сберегаться более значительная абсолютная сумма (если только в то же самое время не произойдут резкие и необычайные изменения в действии других факторов)» (Кейнс, 1978, с.158–159). В другом месте Кейнс так поясняет свою позицию: «Основной психологический закон, в существовании которого мы можем быть вполне уверены не только из априорных соображений, исходя из нашего знания человеческой природы, но и на основании детального изучения прошлого опыта, состоит в том, что люди склонны, как правило, увеличивать свое потребление с ростом дохода, но не в той же мере, в какой растет доход» (Кейнс, 1978, с.157). Сформулированный закон может быть выражен в дифференциальной форме:
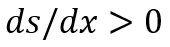 (7)
(7)
где s и x – как и ранее средняя склонность к инвестированию и уровень дохода индивида. В такой трактовке ОПЗН может быть переформулирован следующим образом: с ростом дохода происходит рост средней склонности к инвестированию (накоплению). ОПЗН может быть сформулирован и в альтернативной форме:
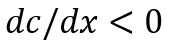 (8)
(8)
т.е. по мере роста дохода происходит снижение средней склонности к потреблению (c).
Закон Кейнса (7) постулирует наличие возрастающей функции средней нормы инвестирования от дохода s=s(x). Тогда для значений дохода xP<xM<xR справедливы следующие неравенства: sP<sM<sR, что и обеспечивает положительность порогового значения ς* в (6), что и требовалось доказать.
Вторым шагом в наших рассуждениях является доказательство достаточности условия теоремы, что эквивалентно обоснованию того факта, что значение коэффициента неравенства ς* может быть больше единицы (т.е. ς*>1); в этом случае решение задачи не только имеет элементарный смысл, но и задает реальное экономическое ограничение. Для этого без потери степени общности предположим, что доля инвестиций описывается нелинейной функцией: s=bxθ, где b и θ – константы; θ задает степень нелинейности процесса роста инвестиционной активности по мере роста дохода. Тогда условие достаточности требует, чтобы выполнялось неравенство:
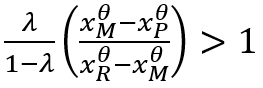 (9)
(9)
Несложно видеть, что при линейной инвестиционной функции, когда θ=1, неравенство (9) превращается в тождественное равенство; в этом случае получаем выражение для среднего дохода, записываемого как взвешенный доход бедных и богатых. Таким образом, линейная функция накопления не несет значимой смысловой нагрузки. В связи с этим имеет смысл рассматривать только нелинейные зависимости. Вместе с тем неравенство (9) выполняется только при θ<1, так как в этом случае рост дохода влечет замедленный рост инвестиционной активности группы богатых субъектов. Следовательно, условие (9) равносильно неравенству:
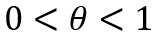 (10)
(10)
Здесь и далее будем говорить, что закон Кейнса выполняется в сильной форме при θ>1 и в слабой форме – при θ<1. В первом случае рост нормы накопления происходит ускоренно, т.е. d2s/dx2>0, тогда как во втором случае – замедленно, т.е. d2s/dx2<0. Если ввести в рассмотрение показатель эластичности инвестиций по доходу E=(x/I)(dI/dx), то для степенной функции накопления будет справедливо равенство E=1+θ. Тогда условие (10) можно переписать в иной форме:
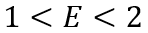 (11)
(11)
Таким образом, в случае проявления ОПЗН в слабой форме с соответствующими условиями (10) или (11) минимальное значение неравенства доходов ς* становится больше единицы и превращается в реальное ограничение при дифференциации общества на два класса. Теорема доказана.
Сформулированная ТИД содержит в себе элемент нетривиальности, так как в соответствии с ней при превышении порогового уровня социального неравенства ς* гетерогенное 2–классовое общество вкладывает в экономическую систему больше инвестиций, чем гомогенное бесклассовое. Однако при малых значениях социального неравенства гомогенное общество может быть даже более привлекательным в плане инвестиционной активности. Схематично этот процесс показан на рис. 2.

Благодаря ТИД мы получили аналитический вывод о том, что чем выше социальное (доходное) неравенство, тем лучше это для сферы инвестирования и производства. Это очень сильное утверждение, причем при его формулировке не использовалось почти никаких дополнительных постулатов и допущений, которые бы ограничивали степень общности полученного аналитического результата. В качестве главного условия, гарантирующего выполнение ТИД, выступает ОПЗН Кейнса в слабой форме.
Теорема об инвестиционном доминировании и закон Кейнса в исторической ретроспективе
Сформулированная ТИД позволяет по-новому посмотреть на процесс выхода человечества из МЛ. Как оказывается, действительно принципиально важным фактором стал рост неравенства доходов населения и образование классового общества на основе капиталистических принципов. Рис. 2 показывает, что гомогенное общество с низким доходом само по себе способно порождать некую инвестиционную ловушку, когда имеющийся низкий доход равномерно расходуется на потребление, а на накопление средств почти не остается. Доходное неравенство меняет ситуацию, но вместе с этим создает антисоциальный эффект, когда инвестиционная нагрузка ложится на класс богатых людей, позволяющих себе инвестировать почти весь свой доход за счет тотального обнищания и маргинализации остальной части населения, оказывающейся на или даже за гранью физического выживания. Однако именно этот исходный пункт служил стартом долгосрочного экономического роста с последующим построением общества всеобщего благосостояния.
Сказанное позволяет дать дополнительную характеристику феномена МЛ, которая совмещает в себе четыре вида экономической ловушки – ловушку стагнации (почти полное отсутствие экономического роста), ловушку бедности (отсутствие роста низкого уровня жизни), инвестиционную ловушку (нехватка инвестиций для нужд производства) и технологическую ловушку (вялая диффузия технологий и отсутствие технического прогресса). Не удивительно, что выход из МЛ стал поворотным пунктом в истории человечества.
Теперь попытаемся ответить, почему эффект от ТИД проявился только при переходе от Средневековья к Новому Времени. Дело в том, что достаточным условием ТИД является закон Кейнса в слабой форме, который носит всеобщий характер. Если же МЛ сохранялась на протяжении многих веков, то, следовательно, и ОПЗН в нужном виде какое-то время не действовал. В этом случае мы приходим к некоему логическому противоречию, которое для определенности будем называть парадоксом В. Полтеровича. Согласно этому парадоксу, классы существовали всегда и всегда были очень богатые люди (например, махараджи в Индии), но они не инвестировали свои капиталы в производственную активность, предпочитая наращивать личное потребление. Следовательно, закон Кейнса не универсален, а социальное неравенство само по себе не является стимулом экономического роста [2]. Как можно объяснить данное противоречие в свете сформулированной ТИД?
Дело в том, что ОПЗН применим к обществу, в котором имеется класс частных инвесторов. К таковым относятся лица, которые имеют избыточные денежные средства и возможность вложить их в любой бизнес–проект без ущерба для общества и без фатальных последствий для себя. Как это ни странно, но такие люди в Средневековье практически отсутствовали. Сошлемся в этой связи на Ж. Ле Гоффа, который раскрывает этимологию слово «богач» в период раннего средневековья и констатирует, что данное понятие означало скорее «сильный», чем «состоятельный» (Ле Гофф, 2015, с.17). Продолжая эту мысль, следует обратить внимание на то, что богатыми людьми были, прежде всего, феодалы. Однако их богатство было институциональным – в форме казны подвластной им территории. Это означает, что средневековые сеньоры, равно как и короли, имели по тем временам огромные богатства, но эти богатства имели форму бюджета региона или страны и, следовательно, могли быть использованы на текущие нужды данной территории, а не для рискованных вложений в бизнес–проекты. Можно сказать, что средневековые богачи были институциональными магнатами со «связанными» денежными ресурсами.
Такая специфика феодального богатства делала капиталы сеньоров иммобильными и не позволяла им распоряжаться этими суммами по своему усмотрению без риска навлечь на себя недовольство масс и элит. Классическим проявлением подобного конфликта может служить синдром Тадх–Махала, который представляет собой поразительно яркий стилизованный пример парадокса Полтеровича. Суть синдрома Тадх–Махала представляет собой инцидент, связанный с мавзолеем Тадж–Махал, построенному по приказу падишаха империи Бабуридов Шах–Джахана в память о жене Мумтаз–Махал. Огромные траты на строительство комплекса в 1632–1653 гг. истощили казну правителя, что спровоцировало или, по крайней мере, ускорило его свержение с престола собственным сыном – Аурангзебом. В данном случае мы сталкиваемся с ситуацией волевого нецелевого расходования государственной казны. Такие действия по превращению текущих финансовых активов в инвестиционный ресурс вызвали недовольство подданных и активизацию политических оппонентов, закончившихся для Шах–Джахана негативным образом.
Разумеется, определенная свобода монархов по реализации инвестиционных проектов была, но крайне ограниченной. Напомним, что даже экспедиции Колумба были профинансированы испанской короной лишь частично; остальные деньги пришлось собирать у частных лиц. Одна из причин многочисленных отказов королей от экспедиций Колумба состояла в наличии альтернативных затрат казны, например, на ведение дорогостоящих войн. Наличие частных магнатов в Испании все-таки позволило организовать колонизацию Америки, однако сами трудности этой кампании показывают, что в Европе к концу XV в. еще не было класса полноценных инвесторов. Все это делало проявление закона Кейнса чрезвычайно слабым, а норму инвестирования у богатых людей крайне невысокой. При таких параметрах даже высокая дифференциация личных доходов не позволяла заметно повысить инвестиционную активность богатой прослойки и выйти из МЛ. Социальное неравенство превратилось в ту силу, которая способствовала преодолению феномена МЛ, несколько позже, когда достиг некоторой зрелости процесс первоначального накопления капитала, оформился класс частных инвесторов и появились рынки со сверхвысокой рентабельностью (Балацкий, Екимова, 2016). ТИД говорит о том, что и закон Кейнса имеет эволюционное звучание в том смысле, что он начинает играть заметную роль только на более зрелых этапах исторического развития; до этого времени его слабое проявление могло порождать парадокс Полтеровича.
Теорема об инвестиционном доминировании: экспериментальные расчеты
Сформулированная ТИД позволяет уяснить качественные моменты в расслоении общества и изменении инвестиционной активности. Вместе с тем необходимо иметь представление и о количественных эффектах, например, понимать, насколько серьезным является требование в виде критической границы (6). Для этого осуществим иллюстративные расчеты, для чего будем рассматривать доходы двух групп российского населения в 2016 г. – десятого дециля (богатые) и девяти первых децилей (бедные). Расчеты на основе данных Росстата позволяют получить следующие данные о среднемесячных доходах: xP=23,8 тыс. руб., xM=30,7 тыс. руб., xR=93,3 тыс. руб. Уточним, что в данном случае xP – средний доход населения девяти первых децильных групп, тыс. руб., xR – средний доход населения десятой децильной группы, а xM – средний доход всего населения страны. В дальнейшем приведенные данные о доходах переводятся годовые величины в долларовом исчислении по обменному курсу 65 руб./долл.; вектор новых значений: xP=4,4 тыс. долл., xM=5,7 тыс. долл., xR=17,2 тыс. долл. Для рассматриваемого примера доля бедного населения λ=0,9.
Чтобы проверить действие ТИД, воспользуемся, как и ранее, степенной функцией вида s=bxθ. При этом в экспериментальных расчетах будем варьировать степенной параметр θ, а для лучшей калибровки получаемых результатов параметр b определим из условия: b=s(xM)–θ. Такой подход позволяет осуществить своеобразную центровку расчетов относительно средней нормы накопления для всего населения. Результаты расчетов приведены в табл. 1.
Таблица 1
Параметр социального неравенства ς* для разных функций накопления
|
Входные параметры |
Выходные параметры |
||||
|
θ |
b |
xP, % |
xM, % |
xR, % |
ς* |
|
1,20 |
2,7 |
16,2 |
22,0 |
83,3 |
0,9 |
|
0,70 |
6,5 |
18,4 |
22,0 |
47,8 |
1,3 |
|
0,50 |
9,2 |
19,4 |
22,0 |
38,3 |
1,5 |
|
0,20 |
15,5 |
20,9 |
22,0 |
27,5 |
1,8 |
|
0,05 |
20,2 |
21,7 |
22,0 |
23,3 |
2,0 |
Расчеты подтвердили теоретический вывод о том, что социальное неравенство начинает выступать в качестве значимого фактора экономического развития только при слабом проявлении закона Кейнса. Однако, помимо этого данные табл. 1 позволяют уяснить масштаб такого влияния, чего нельзя сделать на теоретическом уровне. В частности, мы видим, что даже при чрезвычайно низкой эластичности инвестиций по доходу, когда E=1,05, минимальный барьер неравенства доходов является совершенно незначительным – в районе 2–кратного превышения заработков богатых по сравнению с бедными. Данное пороговое значение на практике почти всегда преодолевается. Например, для наших данных применительно к России 2016 года коэффициент неравенства составляет 3,9, что почти вдвое выше идентифицированного предельного барьера ς*. Таким образом, внутренняя логика процесса инвестирования порождает весьма несущественное ограничение на феномен социальной справедливости, требуя лишь самого незначительного доходного неравенства.
Хотя прикладные расчеты показывают, что ТИД не выступает в качестве драматичного ядра процесса социальной структуризации, вопрос о выгоде общества от доходного неравенства остается открытым. В связи с этим рассмотрим тот выигрыш, который получает общество от наличия классового общества с неравномерным распределением дохода. Для этого оценим величину коэффициента инвестиционного доминирования Ω, который представляет собой отношение объема инвестиций 2-классового и бесклассового общества Ω=IHE/IHO или в развернутом виде:
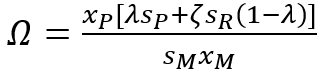 (12)
(12)
Для лучшего понимания количественных эффектов, возникающих при расслоении общества на доходные группы, рассмотрим два сценария – реальный, в котором ζ=3,9 и эта величина соответствует положению дел в России в 2016 г., и гипотетический, в котором коэффициент неравенства увеличивается до ζ=6,0 при сохранении общего дохода населения. Для второго сценария значение среднего дохода сохраняется xM=5,7 тыс. долл., а минимальный и максимальный доход принимают значения: xP=3,8 тыс. долл., xR=22,7 тыс. долл. Подчеркнем, что для данной задачи форма выполнения закона Кейнса не имеет значения в том смысле, что при любом его проявлении возникает универсальный эффект инвестиционного доминирования гетерогенного общества. Результаты расчетов приведены в табл. 2.
Таблица 2
Коэффициент инвестиционного доминирования, %
|
Склонность к инвестированию θ |
Коэффициент доминирования Ω |
|
|
ς*=3,9 |
ς*=6,0 |
|
|
0,05 |
100,8 |
101,7 |
|
0,20 |
104,1 |
108,1 |
|
0,50 |
114,1 |
128,9 |
|
0,70 |
124,2 |
150,7 |
|
1,20 |
166,1 |
247,9 |
|
1,30 |
178,9 |
277,8 |
Полученные цифры недвусмысленно показывают, что серьезный выигрыш от социального неравенства образуется при сильном действии закона Кейнса. В этом случае дополнительная порция инвестиций составляет 80–180% от уровня гомогенного общества, что является серьезной величиной и имеет заметные макроэкономические последствия. В случае слабого проявления ОПЗН инвестиционный выигрыш, наоборот, фактически отсутствует; по крайней мере, он становится значимым только при довольно большом неравенстве. В данном случае хорошо просматриваются источники парадокса Полтеровича – высокое доходное неравенство не дает результатов для инвестиционного рынка из-за чрезмерной склонности богатого сословия к потреблению.
В целом выполненные построения позволяют сделать следующие выводы.
Во-первых, в условиях действия закона Кейнса в сильной форме возникновение классового общества с высоким уровнем доходного неравенства ведет к заметному увеличению инвестиционных ресурсов общества. Расчеты показывают, что емкость инвестиционного рынка гомогенного общества после подобной трансформации может увеличиться в 2–3 раза, что соответствует качественно иному уровню инвестиционной и экономической активности. В связи с этим утверждение о том, что рост социального неравенства явился одним из важнейших факторов преодоления человечеством ИЛ (Попов, 2012), можно считать валидным. Однако к данному тезису следует добавить, что необходимым условием подобного прогресса является большой коэффициент нелинейности θ в функции накопления. Можно сказать, что в данном случае реализуется формула «доходное неравенство – рост инвестиционной активности», когда второй – позитивный – результат компенсирует первый – негативный – эффект.
Во-вторых, в случае действия закона Кейнса в слабой форме, когда богатое сословие не склонно наращивать инвестиционную активность, возникновение классового общества дает инвестиционный выигрыш только при превышении некоторого минимального уровня социального неравенства. Однако прикладные расчеты показывают, что подобное ограничение является несущественным, так как требует поддержания коэффициента неравенства ζ не более 2. Таким образом, ТИД и соответствующая ей нижняя граница неравенства не являются серьезным препятствием для экономического развития. В данном режиме реализуется ослабленный вариант формулы «доходное неравенство – рост инвестиционной активности», когда второй эффект слабо компенсирует первый.
В-третьих, ОПЗН в слабой форме способен выступать в качестве фактора нейтрализации выгод от социальной дифференциации. В этом случае рост доходов богатых людей не ведет к росту инвестиционной активности и продуцирует парадокс Полтеровича. В этом случае действует
формула «доходное неравенство – отсутствие инвестиционной активности», когда второй эффект становится негативным и отчасти усиливает проявления первого.
Модель экономического роста с учетом фактора социального неравенства
ТИД показывает влияние социального неравенства на развитие экономики применительно к инвестиционной сфере. Однако еще более важным и интересным представляется аналитическое продолжение начатой линии для получения явной зависимости темпов экономического роста от параметра социального неравенства. Для этого рассмотрим три фундаментальных уравнения. Первое основано на уравнении накопления основного капитала и выглядит следующим образом (Балацкий, Екимова, 2016):
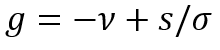 (13)
(13)
где s=sM=I/X – средняя склонность к инвестированию; I – объем инвестиций в основной капитал; X – доход страны (валовой национальный продукт – ВВП); σ – капиталоемкость производства, σ=K/X; K – объем основного капитала в национальной экономике; ν – среднегодовая норма выбытия основного капитала; g – темп экономического роста. Уравнение (13) задает стандартное уравнение экономического роста, продуцируемое накоплением капитала. Учитывая предыдущие обозначения, средняя склонность к инвестированию s в модели (13) тождественна ранее введенной переменной sM, т.е. s=sM.
Второе уравнение, важное для дальнейшего анализа, является структурным соотношением для объема инвестиций:
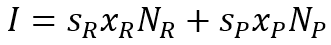 (14)
(14)
Уравнение (14) задает баланс инвестиций за счет бедных и богатых групп населения.
Третье уравнение задает баланс между тремя видами дохода с учетом уровня социального неравенства ζ, т.е. xR=ζxP:
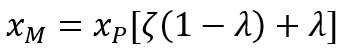 (15)
(15)
Если предположить отсутствие экономического роста g=0, то несложно получить пороговое значение ς**:
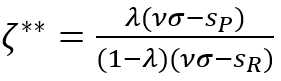 (16)
(16)
При ς>ς** обеспечиваются положительные темпы экономического роста, в противном случае экономика скатывается в режим рецессии. Это означает, что в экономической системе имеется нижний порог доходного неравенства, при котором оказывается возможен экономический рост: g>0 при ζ>ζ**. Данный результат представляет собой не что иное, как аналог ТИД, только применительно к темпам экономического роста. В связи с этим можно сформулировать следующее утверждение об экономическом росте (УЭР):
Утверждение: В условиях слабого действия основного психологического закона накопления Кейнса экономический рост имеет место только при достаточно высоком уровне социального неравенства ζ>ζ**.
Нельзя не обратить внимание на то обстоятельство, что столь нетривиальный нелинейный эффект возникает, как и в случае с ТИД, без каких-либо сильных априорных предположений. Вместе с тем, полученный результат достаточно категоричен и подразумевает необходимость не просто создания 2–классового общества, но и поддержание достаточно высокого неравенства доходов между классами бедных и богатых. В противном случае экономика рискует оказаться в режиме стагнации.
Экономический рост и социальное неравенство: экспериментальные расчеты
Чтобы проиллюстрировать утверждение предыдущего раздела и до конца выяснить роль закона Кейнса для экономического роста и социального неравенства, проведем экспериментальные расчеты для российской экономики с учетом разных параметров степенной функции накопления. Для экономики России последних лет – 2008–2018 гг. – средняя капиталоотдача составляла 2,02, а норма выбытия основного капитала 10,5%. Результаты расчетов по формуле (16) приведены в табл. 3.
Таблица 3
Параметр социального неравенства ς** для разных функций накопления
|
Входные параметры |
Результат |
||||
|
θ |
sP, % |
sR, % |
ν |
σ |
ζ** |
|
0,13 |
21,28 |
25,41 |
0,11 |
2,02 |
0,15 |
|
0,10 |
21,44 |
24,58 |
0,11 |
2,02 |
0,62 |
|
0,08 |
21,55 |
24,04 |
0,11 |
2,02 |
1,09 |
|
0,05 |
21,72 |
23,26 |
0,11 |
2,02 |
2,24 |
|
0,03 |
21,83 |
22,74 |
0,11 |
2,02 |
3,65 |
В данном случае, как и в ТИД, можно видеть, что реальный нижний барьер социального неравенства возникает только при действии закона Кейнса в слабой форме. Более того, как и ранее этот барьер не является слишком высоким и начинает становиться чувствительным для реальной экономики только при чрезмерной склонности богатого сословия к потреблению. Таким образом, в УЭР мы имеем почти полный эквивалент ТИД. Следовательно, для общества с крайней низкой чувствительностью накопления к доходу является не только полезным, но и необходимым образование классов для запуска спирали экономического роста.
Теперь постараемся уяснить степень чувствительности экономического роста к социальному неравенству. Как уже было сказано выше, во многих случаях дифференциация доходов не является обязательным условием экономического роста, однако в большинстве случаев оно может порождать стимулирующий эффект. Для конструктивного ответа на этот вопрос оценим темпы экономического роста по формуле (13) для двух ранее сформированных сценариев – реального с параметром неравенства ζ=3,9 и гипотетического с параметром ζ=6,0 при сохранении общего дохода населения. Результаты расчетов приведены в табл. 4, где первые пять вариантов характеризуют реальные сценарии, а вторые пять – гипотетические.
Таблица 4
Темпы экономического роста в условиях социального неравенства
|
Входные параметры |
Результат |
|||
|
θ |
ν |
σ |
ζ |
g, % |
|
0,05 |
0,10 |
2,02 |
3,9 |
0,48 |
|
0,30 |
0,10 |
2,02 |
3,9 |
1,12 |
|
0,50 |
0,10 |
2,02 |
3,9 |
1,91 |
|
1,10 |
0,10 |
2,02 |
3,9 |
6,39 |
|
1,20 |
0,10 |
2,02 |
3,9 |
7,55 |
|
0,05 |
0,10 |
2,02 |
6,0 |
0,48 |
|
0,30 |
0,10 |
2,02 |
6,0 |
1,22 |
|
0,50 |
0,10 |
2,02 |
6,0 |
2,30 |
|
1,10 |
0,10 |
2,02 |
6,0 |
9,51 |
|
1,20 |
0,10 |
2,02 |
6,0 |
11,57 |
Полученные результаты позволяют сделать целый ряд выводов.
Во-первых, потенциальные темпы экономического роста имеют огромную вариативность в зависимости от свойств функции накопления. Рост параметра θ приводит к росту темпов g на порядок. По всей видимости, образование классов в период позднего средневековья и увеличение склонности к инвестированию богатого сословия, постепенно превращавшегося в класс инвесторов, дало колоссальный импульс к росту инвестиционной активности и послужило важнейшим фактором ускорения экономического роста и выхода из МЛ.
Во-вторых, рост доходного неравенства сам по себе может выступать в качестве важного элемента экономического стимулирования. Например, при крайне высокой склонности к инвестированию увеличение коэффициента неравенства с 3,9 до 6,0 позволяет повысить потенциальные темпы экономического роста с 7,55% до 11,57%. Это означает, что рост неравенства на 1 пункт порождает 2 дополнительных пункта в темпе прироста ВВП, что никак нельзя игнорировать в качестве макроэкономического резерва. Вместе с тем данный стимулирующий эффект почти полностью нивелируется при малых значениях θ. В этом смысле можно утверждать, что истинным драйвером экономического роста является высокая склонность к накоплению, а не неравенство доходов. Второе, как правило, выступает в качестве необходимого условия, а первое – в качестве достаточного. В данном случае мы видим истинную роль социального неравенства и его «вспомогательное» значение для активности экономической системы.
В-третьих, чувствительность темпов экономического роста к масштабу социального неравенства сильно возрастает по мере усиления закона Кейнса. Это означает, что концентрация доходов в руках богатого сословия не ведет к активизации экономического роста при низких значениях θ. Для такого экономического режима велика опасность получить социальную напряженность из-за высокого доходного неравенства без заметного выигрыша в темпах роста производства.
Экономический рост и социальное неравенство: эмпирические оценки
Выше мы осуществляли экспериментальные расчеты для широкого спектра значений функции накопления; далее мы определим истинную зону параметра θ. Для этого построим эконометрическую зависимость между нормой инвестирования и душевым ВВП по ППС в постоянных ценах 2011 г. на данных международной статистики. В этих целях рассмотрим достаточно репрезентативную группу из 22 стран: Финляндия, Норвегия, Дания, Швеция, Испания, Португалия, Франция, Германия, Австрия, Швейцария, Ирландия, Голландия, Бельгия, Словакия, Венгрия, Польша, Хорватия, Литва, Россия, Канада, Япония, Израиль. Все показатели брались как среднее арифметическое за 2008–2017 гг. Как и ранее, s – средняя норма инвестирования, т.е. s=I/Y, где I и Y – инвестиции в основной капитал и ВВП соответственно. Показатель душевого ВВП y=Y/N, где N – численность населения, играет роль среднего дохода xM в предыдущих обозначениях. Полученная эконометрическая зависимость имеет вид:
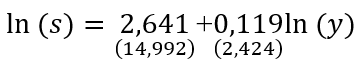 (17)
(17)
N=22; R2=0,22; BP=0,43,
где BP – тест Бройша–Пагана на наличие гетероскедастичности для используемой пространственной выборки стран; все статистические характеристики модели (17) являются удовлетворительными.
На основе модели (17) восстановленная функция накопления s=bxθ имеет окончательный вид: s=e2,641y0,119. Следовательно, для рассматриваемой группы стран имеет место степенная функция накопления с параметром θ=0,119<1. Это означает, что в данных странах закон Кейнса действует в слабой форме, т.е. предельная склонность экономических агентов к инвестированию является крайне низкой. Расчеты показывают, что для России, которая входит в рассматриваемую группу стран, потенциальный темп экономического роста составляет g=0,63%. Это довольно скромная величина, в связи с чем правомерен вопрос: как и на сколько можно повысить темп роста экономики?
В нашей модели есть два параметра, которые в той или иной степени могут быть изменены – коэффициент социального неравенства ζ и показатель капиталоемкости σ. В связи с этим рассмотрим два сценария – реальный с параметром неравенства ζ=3,9 и гипотетический с параметром ζ=6,0. Внутри каждого из сценариев рассмотрим три варианта параметра σ в предположении, что капиталоемкость производства может быть снижена за счет внедрения новых технологий. Результаты расчетов приведены в табл. 5.
Таблица 5
Темпы экономического роста в России для разных сценариев развития
|
Входные параметры |
Результат |
||
|
ν |
σ |
ζ |
g, % |
|
0,105 |
2,02 |
3,9 |
0,62 |
|
0,105 |
1,85 |
3,9 |
1,65 |
|
0,105 |
1,75 |
3,9 |
2,35 |
|
0,105 |
2,02 |
6,0 |
0,63 |
|
0,105 |
1,85 |
6,0 |
1,65 |
|
0,105 |
1,75 |
6,0 |
2,34 |
Полученные результаты показывают, что рост дифференциации доходов не дает практически никаких преимуществ при сложившихся параметрах функции накопления, тогда как рост эффективности основного капитала способен оказать заметное стимулирующее действие на экономическую активность системы. Таким образом, технологический прогресс остается в качестве основного фактора экономического роста; сдвиги в доходной структуре общества не имеют решающего значения.
Заключение
Проведенные расчеты показали, что институт доходного неравенства сам по себе не может выступать в качестве источника экономического роста, что и подтверждается всей историей до капитализма. Как оказывается, неравенство способно активизировать инвестиционные процессы только при наличии своеобразного экономического катализатора – закона Кейнса в слабой форме, который задает нижний порог неравенства. В этом случае неравенство доходов как бы компенсирует низкую активность класса инвесторов. С этой точки зрения институт неравенства действительно имеет значение и в ряде случаев способен сдвинуть экономическую систему с мертвой точки. Вместе с тем все расчеты показывают, что нижний порог неравенства доходов имеет, как правило, символическое значение и редко, когда становится серьезным ограничением экономического роста.
Если закон Кейнса проявляется в сильной форме, то нижний барьер социального неравенства не имеет смысла, а верхний ничем не ограничен. В этом случае ОПЗН выступает уже не в качестве компенсатора пассивности инвесторов, а акселератором их активности. В этом случае ускорение экономического роста может быть принципиальным. В связи с этим есть все основания полагать, что институт неравенства доходов в совокупности с действием закона Кейнса в сильной форме имели решающее значение для выхода Европы из МЛ.
Литература
Балацкий Е.В. (2013). Институциональная дилемма в период первоначального накопления капитала // Журнал экономической теории, 4, 58–69.
Балацкий Е.В., Екимова Н.А. (2016). Внешнеторговый фактор в ликвидации мальтузианской ловушки / В сб.: Экономическая теория и хозяйственная практика: глобальные вызовы. Материалы международной конференции «Эволюция международной торговой системы: проблемы и перспективы – 2016». СПб.: Санкт–Петербургский государственный университет,165–172.
Гершман Б.А. (2009а). Неравенство доходов и экономический рост: обзор эконометрических исследований // Экономическая наука современной России, 2, 104–116.
Гершман Б.А. (2009б). Неравенство доходов и экономический рост: теоретический обзор // Экономика и математические методы, 2,19–30.
Кейнс Дж. М. (1978). Общая теория занятости, процента и денег. М.: Прогресс, 494 с.
Ле Гофф Ж. (2015). Средневековье и деньги: очерк исторической антропологии. СПб.: ЕВРАЗИЯ, 224 с.
Попов В.В. (2012). Почему Запад разбогател раньше, чем другие страны, и почему Китай сегодня догоняет Запад? Новый ответ на старый вопрос // Журнал Новой экономической ассоциации, 3(15), 35–64.
Юревич М.А. (2019). Социальное неравенство, инвестиции и экономической рост // Вопросы регулирования экономики, 10(4), 35–46.
Ahluwalia M. (1976). Income Distribution and Development: Some Stylized facts // American Economic Review, 66(2), 128–135.
Anand S., Kanbur S. (1993). The Kuznets Process and the Inequality-Development Relationship // Journal of Development Economics, 40(1), 25–52.
Aoki S., Nirei M. (2016). Pareto Distribution of Income in Neoclassical Growth Models // Review of Economic Dynamics, 20, 25–42.
Arestis Ph., Baltar C.T. (2017). Income Distribution and Economic Growth: A Critical Approach // Panoeconomicus, 64(2), 125–138.
Behringer J., van Treeck T. (2019). Income Distribution and Growth Models: A Sectoral Balances Approach // Politics & Society, 47(3), 303–332.
Berg A.G., Ostry J.D. (2017). Inequality and Unsustainable Growth: Two Sides of the Same Coin? // IMF Economic Review, 65, 792–815.
Clarke G. (1992). More Evidence on Income Distribution and Growth // Country Economics Department, The World Bank, WPS 1064, 1–28.
Dutt A.K. (2017). Heterodox Theories of Economic Growth and Income Distribution: A Partial Survey // Journal of Economic Surveys, 31(5), 1240–1271.
Kaldor N. (1956). Alternative theories of distribution // Review of Economic Studies, 23(2), 83–100.
Kuznets S. (1955). Economic Growth and Income Inequality // American Economic Review, 45(1), 1–28.
Milanovic B. (2016). Why might the rich be indifferent to income growth of their own countries? // Economics Letters, 147(C), 108–111.
Onaran O., Galanis G. (2014). Income distribution and growth: a global model // Environment and Planning A, 46(10), 489–2513.
Robinson S. (1976). A Note on the U-hypothesis Relating Income Inequality and Economic Development // American Economic Review, 66(3), 437–440.
Sakaki S. (2017). Income distribution management to sustain long-term economic growth: does the equalization of income distribution contribute to long-term economic growth? // Evolutionary and Institutional Economics Review, 14, 363–395.
Tavani D., Zamparelli L. (2018). Growth, Income Distribution, and the ‘Entrepreneurial State’ // Journal of Evolutionary Economics, January, 1–32.
[1] В рамках данной статьи социальное неравенство мы будем рассматривать в узком смысле – как неравенство в доходах населения.
[2] Данные аргументы были высказаны В. Полтеровичем автору в одной из частных бесед, а также на многочисленных научных семинарах.
Официальная ссылка на статью:
Балацкий Е.В. Институт социального неравенства и экономический рост // «Журнал институциональных исследований», Том 12, №1, 2020. С. 66–83.