Введение. Инфляция продолжает оставаться важным фактором экономического роста и благосостояния населения, в связи с чем она постоянно находится в зоне самого пристального внимания как регулирующих органов, так и сообщества аналитиков. Данный параметр нуждается не только в постоянном оперативном мониторинге, но и в перманентном прогнозировании. Это связано с тем обстоятельством, что почти все экономические агенты закладывают фактор будущей инфляции в текущие цены, тем самым страхуя себя от возможных потерь; похожие процедуры осуществляют и государственные органы при планировании индексации пенсий и зарплат работников бюджетной сферы.
Одна из традиционных проблем прогнозирования инфляции связана с ее волатильностью, неравномерностью и многофакторностью, а также с инструментальным плюрализмом ее моделирования. Применительно к России данные аспекты имеют следующие проявления.
Во-первых, краткосрочное (помесячное) прогнозирование инфляции порождает эффект, который получил название фундаментальной проблемы атрибуции данных в макромоделях (ПАДМ) [1]. Данный эффект связан с тем обстоятельством, что среднемесячные величины индекса потребительских цен (ИПЦ) в России за 2017–2018 гг. составляли порядка 0,2%. По отношению к этой микроскопической цифре любые ошибки оказываются не просто заметными, а недопустимо большими. Указанное глубинное противоречие между макроэкономическим характером конструируемых моделей и микроэкономической величиной моделируемой величины не может быть преодолено простым усовершенствованием эконометрических моделей.
Во-вторых, практически вся потенциальная волатильность феномена инфляции уходит в область краткосрочных флуктуаций ИПЦ. Так, модельные расчеты по российским данным за 2017–2018 гг. показывают, что среднемесячная ошибка аппроксимации моделируемой инфляции в 6–7 раз превосходит величину среднегодовой ошибки [2]. Тем самым волатильность процесса роста цен в России распределена преимущественно внутри анализируемых лет по месяцам, в связи с чем составление именно краткосрочных прогнозов представляет собой ключевую инструментальную проблему.
В-третьих, модельные расчеты показывают, что феномен инфляции из сугубо монетарного превращается в преимущественно немонетарное явление [2]. В прикладных моделях доминантой инфляции выступают уже, как правило, немонетарные факторы.
В-четвертых, в настоящее время моноинструментальные подходы к прогнозированию инфляции практически утратили свою актуальность и применяются, в основном, в составе комплексного моделирования. Наряду с «параллельным» использованием разных классов моделей с последующим усреднением их результатов сегодня строятся гибридные модели, в которых происходит «последовательное» объединение моделей разного тапа. Иными словами, трендом в прогнозировании инфляции является переход от моноинструментального моделирования к полиинструментальному.
Указанные особенности нынешнего этапа моделирования инфляции являются во многом универсальными, т.е. справедливыми для разных стран и довольно длительного ретроспективного периода. Цель данной статьи состоит в построении гибридной прикладной модели инфляции, которая обладает упреждающим свойством и позволяет осуществлять краткосрочные прогнозы с достаточно высокой точностью. Новизна подхода состоит в 4–ступенчатой процедуре построения модели и гибкой системе прогнозирования на ее основе.
Практика построения гибридных моделей. Не будет ошибкой сказать, что сегодня наметился новый инструментальный тренд, сущность которого состоит в построении гибридных модельных конструкций в целях прогнозирования различных процессов и явлений.
Идея построения горизонтальных гибридных моделей в прогнозных целях первоначально была обоснована в 1969 году Дж. Бейтсом и К. Гренджером в работе [3] и в дальнейшем развита П. Ньюболдом и К. Гренджером [4]. Экономисты предложили повышать точность прогнозных оценок за счет усреднения прогнозов нескольких статистических моделей. К настоящему времени уже накоплен огромный арсенал моделей инфляции, которые используются в регулятивной практике центральных банков, включая Банк России (подробный анализ см. в [5]). Опыт их использования показывает, что один тип модели уже практически не используется регулятором; расчеты проводятся на базы разных моделей, после чего они усредняются в целях повышения их точности и объективности. Тем самым осуществляется горизонтальный синтез модельных прогнозов как разновидность гибридного моделирования.
Дальнейшее развитие методов построения гибридных моделей осуществлялось по двум направлениям: либо путем разработки новых методов объединения прогнозов, либо посредством вертикального синтеза – посредством расширения комбинированной конструкции, предложенной Дж. Бейтсом, К. Гренджером и П. Ньюболдом, за счет новых видов индивидуальных моделей [6].
В рамках первого направления широкое распространение получило объединение статистических и структурных моделей, особенно сочетание нейронных сетей с эконометрическими моделями типа ARIMA и SARIMA. Так, в работе [7] экспериментальные результаты с реальными наборами данными показали повышение точности прогнозирования при использовании указанного выше сочетания относительно любой из моделей, используемой отдельно. В исследовании [8] продемонстрировано повышение точности прогноза распространения церебральных нарушений при использовании полиинструментальных моделей. Аналогичные результаты, подтверждающие улучшение качества прогнозирования при использовании гибридных моделей, были получены и в отношении прогнозных оценок колебаний фондовых индексов [9], энергетической нагрузки [10], почасовых температур [11] и др.
Не делая акцент на перечислении подобных работ, укажем лишь, что их число уже достаточно велико и продолжает расти. Главным трендом всех последних исследований является использование полиинструментальной методологии, когда окончательный прогноз формируется на основе синтеза разнотипных моделей. В этом же русле идут авторы данной статьи, предлагая гибридный аналитический комплекс прогнозирования инфляции путем последовательного объединения отдельных классов моделей с возможностью его переналадки в ответ на изменения во внешней среде.
Укрупненная классификация факторов инфляции. В современной литературе используются различные классификации факторов инфляции. Не останавливаясь на этом вопросе подробно, рассмотрим ее наиболее плодотворную версию, которая нашла применение в данном исследовании. Так, окончательная классификация объясняющих переменных предполагает два критерия с двумя альтернативами каждый. Первый критерий учитывает природу объясняющих факторов – монетарные и немонетарные; второй критерий отражает источник происхождения факторов – внутренние, формирующиеся внутри России, и внешние, приходящие извне. Тогда искомая структура входных переменных модели может быть представлена в виде табл. 1.
Таблица 1
Классификация факторов инфляции для моделей (1) и (2)
|
Источник происхождения |
Природа факторов |
|
|
Монетарные |
Немонетарные |
|
|
Внутренние |
ключевая ставка (r) |
цены на картофель (Pot); отношение производительности труда к заработной плате (∆W); индекс потребительских настроений (CSI); индекс предпринимательской уверенности (BCI) |
|
Внешние |
валютный курс (Ex) |
цены на нефть (Oil) |
С теоретической точки зрения искомая модель должна включать факторы из всех указанных в табл. 1 четырех групп. Однако на практике это требование может нарушаться, что не должно восприниматься в качестве недостатка модели. Состав факторов инфляции меняется в зависимости от периода исследования; универсальный набор факторов найти невозможно.
Идеология маркерных моделей инфляции. При изучении инфляции главным ее показателем традиционно выступает индекс потребительских цен (ИПЦ); остальные измерители (например, индекс промышленной инфляции, индекс-дефлятор и др.), как правило, менее точны и надежны, а также могут не иметь помесячной градации. Здесь и далее нами будет ИПЦ в качестве наиболее репрезентативной меры инфляции.
При построении эконометрических моделей прогнозирования инфляции вообще и ИПЦ в частности следует учитывать одно важное обстоятельство. Дело в том, что объясняющие переменные инфляции в общем случае могут быть двух типов – факторы и маркеры. Под факторами инфляции традиционно понимаются показатели, которые отражают непосредственные причины роста цен, тогда как под маркерами подразумеваются некие вспомогательные индикаторы, позволяющие с некоторым упреждением во времени предвидеть рост потребительских цен. Типичным маркером может выступать цена на сырую нефть на мировом рынке.
При таком подходе выходная переменная модели увязывается со своими маркерами, которые сами по себе могут представлять некую разновидность инфляции. В этом случае речь идет о моделировании не глубинных причинных связей, а лишь последовательности связанных событий примерно одинаковой природы. Например, рост цен на сырую нефть сам по себе представляет проявление инфляции, однако происходит раньше, чем рост ИПЦ.
В прикладных моделях прогнозирования инфляции в качестве объясняющих переменных могут фигурировать как факторы, так и маркеры. Используя несколько иную терминологию, можно сказать, что факторы являются диспозиционными характеристиками процесса инфляции, а маркеры – ситуативными. Соответственно, эконометрические модели, в которых присутствуют переменные-маркеры, в дальнейшем будем называть маркерными моделями.
Переход к маркерным моделям обусловлен в основном прикладной направленностью конструируемых зависимостей. Более того, сама идеология маркерных моделей является эффективной исключительно для краткосрочного прогнозирования; для долгосрочных расчетов она теряет смысл.
Из сказанного становится ясно, что маркерные модели включают в себя набор переменных с лагами в несколько месяцев. Именно наличие таких лагов придает конструируемым моделям свойство упреждающей диагностики.
Самостоятельной инструментальной проблемой является поиск и отбор переменных-маркеров, которые следует включать в эконометрические модели. В общем случае в качестве потенциальных маркеров могут выступать цены на любые товары и услуги, каковых даже в официальной статистике насчитываются сотни. Дополнительная сложность учета маркеров состоит в том, что они также не являются универсальными, т.е. те продукты, которые обладали указанным свойством в один период, могут терять его на другом временном отрезке и наоборот.
Четырехшаговая процедура построения гибридной модели инфляции. Для учета специфики нынешней инфляции необходимо построить модель, которая учитывала бы четыре ее свойства, рассмотренные во введении. Для этого можно предложить аналитическую конструкцию, построение которой предполагает четыре шага. Рассмотрим их более подробно.
Первый шаг: унификация модельных переменных. Для построения эконометрической модели ИПЦ маркерного типа используется вспомогательный технический прием, который состоит в переводе всех показателей в месячные индексы роста в процентном выражении. Это позволяет привести все модельные данные в сопоставимые единицы измерения и объединить единой логикой. Попытки использовать в эконометрической модели цены товаров в абсолютном выражении, равно как и величины ключевой ставки и валютного курса, не дали положительных результатов. Можно сказать, что перевод всех данных в индексную форму является первой процедурой их калибровки для дальнейшего эффективного сопряжения в форме эконометрической зависимости.
Второй шаг: отбор активных маркеров. Априори определить переменные-маркеры невозможно в силу уже указанных выше причин. Ситуация осложняется еще и тем обстоятельством, что в статистике Росстата имеется большое число потенциальных маркеров – более 600 товарных групп. Если из этого массива отбросить товары, для которых имеются пробелы за определенные месяцы изучаемого периода, то число переменных, претендующих на роль маркеров, сократится до 454 позиций. Однако даже в этом случае экспериментировать со всеми элементами указанной номенклатуры при построении эконометрической зависимости совершенно невозможно. В связи с этим второй методический шаг представляет собой отбор наиболее активных потенциальных маркеров из их общей массы на основе анализа коэффициентов корреляции между ИПЦ и индексом цен на соответствующий товар для лагов от 1 до 6 месяцев. Итогом такой процедуры является корреляционная матрица ИПЦ и потенциальных маркеров с учетом временного лага (табл. 2), которая позволяет выбрать товары с наибольшим коэффициентом корреляции с соответствующим ему лагом (в табл. 2 для примера приведены только 5 из подлежащих рассмотрению 454 товаров). Применение подобной процедуры позволяет сократить число потенциальных маркеров с нескольких сотен до полутора–двух десятков.
Таблица 2
Корреляционная матрица ИПЦ и потенциальных маркеров с учетом временного лага
|
№ |
Наименование товара |
Величина временного лага, мес. |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
1 |
Легковой автомобиль импортный подержанный |
0,336 |
0,039 |
–0,077 |
–0,165 |
–0,148 |
–0,132 |
|
2 |
Хлеб и булочные изделия из пшеничной муки 1 и 2 сортов |
0,530 |
0,236 |
0,044 |
–0,043 |
0,016 |
–0,009 |
|
3 |
Говядина (кроме бескостного мяса) |
0,563 |
0,297 |
0,169 |
0,165 |
0,115 |
0,117 |
|
4 |
Апельсины |
0,141 |
0,057 |
0,045 |
0,089 |
0,081 |
0,074 |
|
5 |
Бензин автомобильный |
–0,274 |
–0,066 |
0,139 |
0,285 |
0,294 |
0,313 |
Применительно к группе монетарных факторов помимо ключевой ставки и валютного курса рассматривались агрегат денежной массы М2 с ее производными, включая коэффициент монетизации ВВП. Отобранные показатели использовались для построения искомой регрессии.
Третий шаг: отбор эконометрической модели. Построение эконометрической модели осложняется тем фактом, что универсальной зависимости не существует. Фактически для каждого определенного периода времени действует своя модель, в связи с чем необходимо определить и период, который следует использовать для построения прогнозной модели, и окончательную спецификацию (набор переменных) этой модели. Такое положение дел приводит к необходимости проведения экспериментов с длиной ретроспективного ряда и соответствующими эконометрическими зависимостями. Ниже мы рассмотрим данный этап более подробно.
Четвертый шаг: построение нейросетевой модели инфляции. Построенная на предыдущем шаге искомая эконометрическая модель заведомо не позволяет осуществлять прогнозы с необходимой точностью. Учитывая, что месячные темпы инфляции могут составлять около 0,2%, то допустимое отклонение от этой величины не должно превышать 0,02%, что совершенно недостижимо в рамках стандартных макроэкономических моделей роста ИПЦ. В результате возникновения ПАДМ встает задача калибровки прогнозных оценок с доведением ошибки до приемлемого уровня. В этих целях осуществляется процедура построения дополнительной – нейросетевой – модели инфляции на основе переменных, вошедших в прикладную эконометрическую зависимость.
Такая дополнительная процедура обладает целым рядом преимуществ по сравнению с автономным использованием каждого типа инструментария – эконометрической модели и нейронной сети. Во-первых, наличие эконометрической модели позволяет сохранить теоретическую основу моделируемого процесса, очистить его от незначимых факторов («шумов») и ограничиться небольшим числом понятных и хорошо верифицируемых факторов. Последующая чисто механистическая обработка базовой зависимости с помощью нейросети осуществляется уже для теоретически осмысленной зависимости, а не для хаотичного набора огромного числа потенциальных регрессоров. Во-вторых, использование арсенала нейронной сети позволяет существенно повысить точность прогнозов за счет ее обучения без потери объяснительной способности общей модельной схемы. Фактически настройка нейросети и калибровка выходной переменной позволяют «превратить» теоретическую эконометрическую конструкцию в практически значимую модель, способную выдавать адекватные прогнозы. В-третьих, наличие небольшого числа регрессоров в эконометрической модели позволяет максимально экономно использовать вычислительные возможности нейросети и повысить эффективность работы с ней. Данный результат достигается посредством загрузки в нейросеть не сотен и тысяч потенциальных факторов инфляции, а не более десятка регрессоров, уже прошедших статистические тесты и заведомо являющихся значимыми факторами процесса роста цен. Такое резкое усечение входных данных ведет к сокращению промежуточных слоев и числа эпох (экспериментов) в нейросетевой модели. Тем самым нейросеть не перегружается ненужными данными и дает возможность получить нужный результат в более сжатые сроки.
Такая четырехшаговая процедура построения гибридной модели прогнозирования инфляции, являющейся синтезом эконометрической и нейросетевой технологий, лежит в русле современных подходов к прогнозированию экономических процессов. Из сказанного выше совершенно ясно, что изъятие любого этапа из описанной схемы приведет к резкому падению качества прогнозов, чем и обусловлена необходимость гибридной модели.
Выбор эконометрической модели инфляции. Как отмечалось ранее, третий шаг построения гибридной модели инфляции предполагает эксперименты с эконометрическими зависимостями. Забегая вперед, укажем, что нами рассматривались два ретроспективных периода – «полный», четырехлетний (2014–2017 гг.) и «усеченный», двухлетний (2016–2017 гг.). Проведенные вычислительные эксперименты на основе данных за период 2014–2017 гг. с помесячной разбивкой позволили построить следующую базовую модель инфляции:
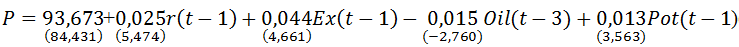 (1)
(1)
N=48; R2=0,755; DW=2,595; E=0,257%,
где P – месячный индекс ИПЦ; r – месячный индекс ключевой ставки; Ex – месячный индекс валютного курса рубль/доллар; Oil – месячный индекс цен на нефть; Pot – месячный индекс цен на картофель; t – индекс текущего месяца. В скобках под коэффициентами регрессии приведены их t–статистики; E – ошибка аппроксимации (в процентах); остальные обозначения – стандартные.
Помимо традиционного фактора инфляции в виде ключевой ставки Банка России в модели (1) присутствуют три рыночных маркера в виде валютного курса рубль/доллар, а также цен на нефть и картофель, которые охватывают все четыре группы табл. 1. При этом временные лаги выявленных маркеров предельно короткие – от 1 до 3 месяцев. Такой набор регрессоров характеризует модель (1) как чрезвычайно удачную с теоретической точки зрения, ибо в ней присутствуют все возможные маркеры с разумным периодом упреждения на фоне достаточно высокого коэффициента детерминации и чрезвычайно малой ошибки аппроксимации.
Отдельного комментария заслуживают знаки коэффициентов модели. Так, рост процентной ставки приводит к росту ИПЦ, что противоречит многолетним утверждениям экспертов Банка России о том, что данный инструмент может и должен использоваться в качестве антиинфляционной меры. Традиционные теоретические представления также говорят о том, что в соответствии с принципом Тейлора рост процентной ставки должен вести к удорожанию денег, их относительному дефициту и стабилизации цен. Модель (1) опровергает эти тезисы, тем самым подтверждая аргументы большого числа других исследователей о том, что ключевая ставка представляет собой неэффективное средство борьбы с инфляцией. Кроме того, в настоящее время многие центральные банки отказались от использования в своей работе данного правила в качестве приоритетного [12]. В работе [13] подробно разбираются причины нарушения принципа Тейлора: в странах с развитой экономикой в результате повышения процентной ставки происходит падение инфляции, тогда как в экономике развивающихся стран рост процентной ставки провоцирует усиление инфляции [14; 15]; обратная связь между рассматриваемыми показателями имеет место в краткосрочном периоде, в то время как в долгосрочной перспективе прослеживается прямо пропорциональная зависимость между ними [16] и т.п. Вместе с тем вывод на основе модели (1) не может быть окончательным в этом споре в силу специфики самой модели, учитывающей в большей мере упреждающие эффекты от рыночных маркеров, а не собственно причины инфляции.
Чрезвычайно интересным представляется связь между ИПЦ и валютным курсом. В данном случае модель (1) фиксирует так называемый эффект переноса [17], т.е. зависимость внутренней инфляции национальной валюты от ее девальвации. Причем девальвация предшествует инфляции, «переливаясь» через 3 месяца в форму открытого роста цен внутри страны. Тем самым модель (1) подтверждает тезис о том, что инфляция и девальвация являются однопорядковыми явлениями, происходят синхронно и должны регулироваться в рамках единой монетарной политики.
Среди рыночных маркеров значимыми оказались картофель, обладающий потенциальным свойством гиффиновского товара, и нефть, рост цен на которую увеличивает доходы российской добывающей промышленности, ведет к росту объема валюты на внутреннем рынке по сравнению с рублевой денежной массой и тем самым способствует стабилизации ИПЦ. Заметим, что расширить построенную модель за счет включения других товарных маркеров не удалось. Так, «претендентами» на включение в модель на базе процедуры отбора активных маркеров (второй шаг построения гибридной модели) выступали легковой автомобиль (импортный, подержанный), апельсины и бензин, однако их интеграция в модель приводила к росту ошибки аппроксимации. Кроме того, важными потенциальными факторами регрессии выступают тарифы на газ, электроэнергию и услуги ЖКХ, которые регулируются государством. Однако их изменения происходят дискретно и довольно редко, после чего тарифы остаются долгое время стабильными. При построении эконометрической модели с шагом в 1 месяц такая «рваная» динамика тарифов не может быть использована, в связи с чем указанные факторы были исключены из рассмотрения. Кроме того, до сих пор остается открытым вопрос о характере взаимовлияния изменения тарифов на услуги естественных монополий и роста индекса цен. С одной стороны, ежегодное повышение тарифов на коммунальные и транспортные услуги вызвано инфляцией предыдущего года, с другой стороны, данное повышение тарифов провоцирует рост цен текущего года. Помимо указанных факторов рассматривались различные монетарные агрегаты – денежная масса М2, коэффициент монетизации ВВП и т.п. Однако эти переменные также оказались незначимыми для конструируемой модели [13].
Построенная модель (1) по своим статистическим характеристикам может быть признана приемлемой для первичного установления детерминант инфляции [1]. Так, на рис. 1 можно видеть, что модельное значение ИПЦ почти идеально повторяет фактическую траекторию инфляции, а линии тренда для двух рядов расходятся совсем незначительно [2]. Однако модель (1) построена для инфляции в форме индексов роста, выраженных в процентах. Это означает, что значения ИПЦ в модели колебались вокруг 100–процентной отметки. Однако на практике оценка инфляции ведется в темпах прироста, которые в помесячном измерении составляют мизерную величину – доли процента. В связи с этим чрезвычайно высокая точность в модели (1) относительно индексов ИПЦ резко падает – на два-три порядка – при переходе к темпам прироста цен. Такое преобразование приводит к возникновению ПАДМ [1]. Так, например, проведенный вычислительный эксперимент, предполагающий прогноз по построенной модели для известных данных за январь–апрель 2018 г., позволил установить, что относительно индекса инфляции ошибка прогноза по месяцам составляет 0,03; 0,12; 0,23 и 0,11%, тогда как относительно темпов инфляции ее величина составляет 10,7; 57,6; 80,3 и 31,1% соответственно; последние три величины являются неприемлемо большими. Таким образом, модель (1), будучи теоретически и статистически безупречной, для скользящих прикладных прогнозов не подходит.
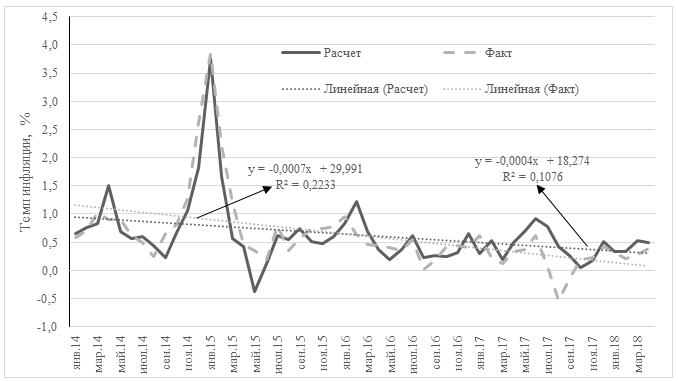
Рис.1. Фактические и расчетные траектории ИПЦ (модель (1))
Указанная проблема атрибуции данных не является единственной при построении модели (1). Для понимания источника возникающих погрешностей рассмотрим накопленную за год ошибку относительно темпов инфляции по модели (1) (табл. 3). Здесь просматривается три интересных факта. Во-первых, для первых двух лет модель (1) устойчиво занижает фактические значения ИПЦ, тогда как для последующих двух лет она дает устойчивое завышение инфляции. Во-вторых, в четвертом году ошибка прогноза на порядок возрастает по сравнению с третьим годом. В-третьих, ошибка за все четыре года чрезвычайно мала. Данные факты свидетельствуют о том, что в течение 4 лет произошло принципиальное изменение режима формирования ИПЦ, каждый из которых длился примерно два года. При этом модель (1) агрегирует эти режимы и в целом хорошо описывает процесс, однако к концу моделируемого периода ошибка начинает нарастать, свидетельствуя о потере адекватности полученной эконометрической зависимости на указанном временном отрезке. Данный факт подводит к пониманию того, что для прикладных целей следует строить модель на более коротком временном интервале, охватывающем 2016–2017 гг. В этом случае есть основания предполагать, что модель будет воспроизводить единообразный режим подавления инфляции, который поддерживался Банком России на протяжении указанных лет.
Таблица 3
Распределение накопленной за год ошибки аппроксимации ИПЦ по моделям (1) и (2), %
|
Годы |
ИПЦ по модели (1) |
ИПЦ по модели (2) |
||||
|
Расчет |
Факт |
Ошибка |
Расчет |
Факт |
Ошибка |
|
|
2014 |
10,2 |
11,3 |
–9,7 |
– |
– |
– |
|
2015 |
10,0 |
12,9 |
–22,2 |
– |
– |
– |
|
2016 |
6,2 |
5,3 |
14,9 |
6,1 |
5,8 |
5,5 |
|
2017 |
5,4 |
2,5 |
116,8 |
2,4 |
2,5 |
–4,5 |
|
Всего |
35,8 |
35,8 |
0,1 |
8,2 |
7,7 |
4,9 |
Проведенные вычислительные эксперименты для периода 2016–2017 гг. дали следующую альтернативную модель инфляции:
.png) (2)
(2)
N=24; R2=0,805; DW=1,397; E=0,116%,
где ∆W – месячный финансово–технологический индекс отношения производительности труда к заработной плате; CSI – индекс потребительских настроений; BCI – индекс предпринимательской уверенности (среди предпринимателей добывающей промышленности); остальные обозначения прежние. Статистические характеристики модели (2) являются удовлетворительными.
Сравнение моделей (1) и (2) показывает, что политика Банка России в 2016–2017 гг. радикально отличалась от мер предыдущего двухлетнего периода, что выразилось в последовательном и интенсивном подавлении инфляции и предопределило совсем иной состав маркеров в модели (2) (табл. 1). В частности, смена режима шла в направлении «вымывания» внешних факторов и маркеров. Как это ни парадоксально, но ни валютный курс, ни сырая нефть не оказывали значимого влияния на внутреннюю инфляцию в рассматриваемый период. Фактически можно констатировать, что Банк России добился того, что инфляция в стране «отвязалась» от традиционных внешних агрегатов. При этом ключевая ставка сохранила свое значение, хотя ее влияние «отдалилось» с 1 месяца в модели (1) до 3 месяцев в модели (2). Смена регулятивного режима Банка России предопределила ограниченность длины ретроспективного ряда для модели (2) (24 наблюдения).
Важным различием моделей (1) и (2) является состав их регрессоров, а именно: их число увеличилось с четырех до пяти, причем все они попадают в группу внутренних. Принципиально изменился характер маркеров, некоторые из которых стали напоминать полноценные факторы инфляции. Среди таковых фигурирует финансово–технологический индекс ∆W, который диагностирует дисбаланс между технологическими сдвигами в производстве (производительностью труда) и финансовыми затратами (уровнем оплаты труда). Примечательным является также появление среди маркеров модели параметров настроений, причем как потребителей, так и производителей.
Нельзя не указать еще на одно принципиальное различие между моделями (1) и (2), состоящее в структуре объясняющих факторов. Так, проведенные расчеты показывают, что в модели (1) интегральный показатель влияния немонетарных факторов составляет 39,5%, тогда как в модели (2) – 75,2% [3]. Таким образом, если в 2014–2015 гг. доминантой процесса инфляции выступала группа монетарных факторов, то в 2016–2017 гг. – группа немонетарных маркеров. Иными словами, даже за последние годы феномен инфляции в России претерпел принципиальную трансформацию, когда в начальный период действия международных санкций он формировался в основном посредством монетарных каналов, а в более поздний период – за счет немонетарных рыночных сил.
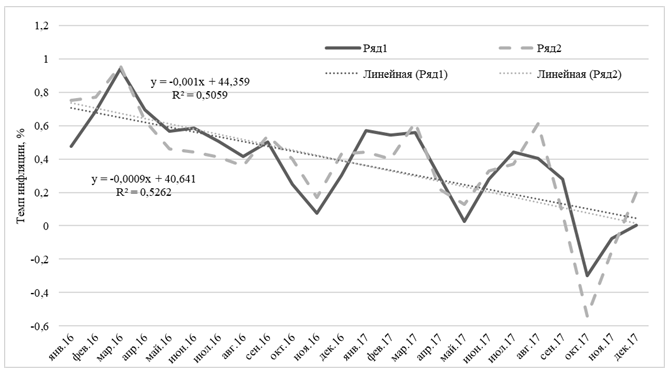
Рис. 2. Фактические и расчетные траектории ИПЦ (модель (2))
Точность модели (2) существенно возросла по сравнению с моделью (1). Так, ошибка по годам, равно как и общая ошибка за два года, находятся в пределах 5–6% (табл. 3), что можно считать хорошим результатом. При этом даже в рамках укороченного периода все-таки просматривается определенная неравномерность моделируемого режима: если в первый год происходит переоценка инфляции, то во второй – ее недооценка. Это связано с замедлением борьбы Банка России с инфляцией в 2017 году. В целом же точность модели такова, что рисунок фактической и прогнозной траекторий ИПЦ практически одинаковый, а их тренды почти полностью совпадают (рис. 2). Во многом улучшение качества модели (2) по сравнению с моделью (1) связано с отбрасыванием периода с характерным для него мощным инфляционным выбросом (рис. 1).
Вычислительный эксперимент с прогнозированием инфляции по модели (2) на три месяца вперед для периода 11.2017–01.2018 показал, что месячная ошибка относительно темпа инфляции составила 28,77, 24,41 и 97,91% соответственно, что по-прежнему выходит за допустимые рамки погрешности. Данный факт говорит о невозможности непосредственного использования модели (2) для прогнозирования и предопределяет дальнейшие поиски способов подавления ошибок для более точного предсказания ИПЦ.
Калибровка модели с помощью нейронной сети. Выше было показано, что главная проблема в прогнозировании ежемесячных темпов инфляции состоит в их малой величине. В литературе уже отмечалось, что данная проблема является неразрешимой в рамках традиционных эконометрических моделей [1]. Сегодня существуют различные способы и технические приемы для «обхода» указанной проблемы. На наш взгляд, наиболее предпочтительным представляется построение «вспомогательной» модели прогнозирования ИПЦ в виде нейронной сети на основе данных уже имеющейся эконометрической зависимости (2).
Можно выделить четыре особенности динамики инфляции в России за рассматриваемые годы. Первая состоит в почти идеальном совпадении фактического и модельного трендов (рис. 2); вторая предполагает наличие сильных флуктуаций фактических значений ИПЦ вокруг тренда, что требует определения прогнозного диапазона темпов инфляции, который не должен «пробиваться»; третья особенность выражается в наличии неявной цикличности колебаний ИПЦ вокруг линии тренда; четвертая связана с увеличением амплитуды колебаний ИПЦ по мере снижения их фактических темпов. Все эти динамические особенности инфляции могут быть учтены хорошо обученной нейросетевой моделью.
Построение прикладной нейронной сети Web–Inf было выполнено в программном продукте RStudio (пакет «neuralnet») для набора переменных модели (2). Пять регрессоров эконометрической модели прошли отбор, в связи с чем в модель Web–Inf загружались только эти переменные, что позволило производить калибровку прогнозных расчетов максимально быстро и эффективно.
Процесс построения сети состоял из двух последовательных этапов. На первом этапе обучение сети велось на основных ретроспективных данных (февраль 2016 г. – октябрь 2017 г.) с использованием критерия минимизации суммы квадратов ошибок. Эта операция предполагала случайное деление выборки на две части без хронологической последовательности: для обучения и для проверки точности. На втором этапе проверка адекватности обученной сети велась на тестовых прогнозных данных, в качестве которых использовались последние три месяца ретроспективного ряда (ноябрь 2017 г. – январь 2018 г.); в качестве критерия точности использовалась минимизация средней абсолютной ошибки прогнозов. Таким образом, искомая нейросеть должна была одновременно соответствовать двум критериям: низкой ошибке на тестовых данных и низкой ошибке на прогнозных данных. В итоге, в процессе подбора было отброшены сотни тысяч нейросетей, проходивших по критерию обучения, но показывавших неудовлетворительные результаты на прогнозной выборке.
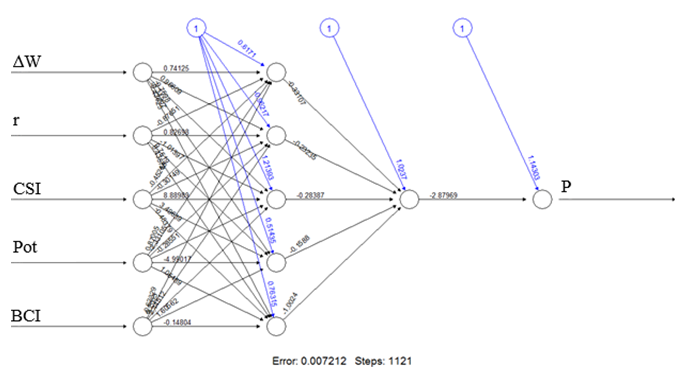
Рис.3. Структура нейронной сети ИПЦ
Для лучшего понимания алгоритма калибровки искомой зависимости «расшифруем» построенную нейросеть на рис.3:
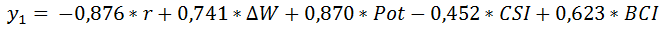 (3)
(3)
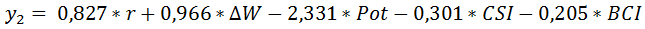 (4)
(4)
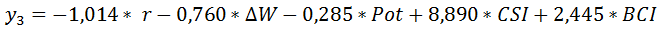 (5)
(5)
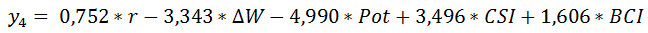 (6)
(6)
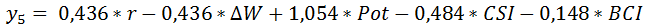 (7)
(7)
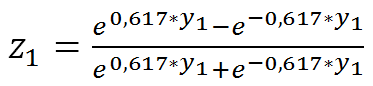 (8)
(8)
.png) (9)
(9)
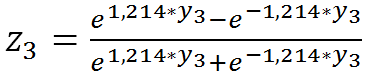 (10)
(10)
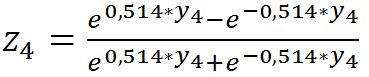 (11)
(11)
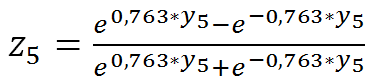 (12)
(12)
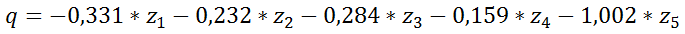 (13)
(13)
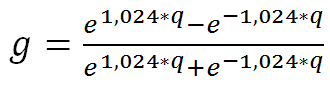 (14)
(14)
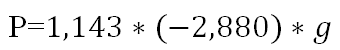 (15)
(15)
Следует отметить, что примененный в исследовании подход не является широко распространенным, поскольку обычно точность прогнозов считается главным признаком качества нейронной сети. В данном случае был усилен традиционный подход посредством добавления двух фильтров точности – основного (по ретроспективным данным) и дополнительный (по тестовым прогнозам). Предварительно все данные модели Web–Inf были нормализированы по стандартной формуле Xnorm=(Х–Xmin)/(Xmax–Xmin). Минимальная средняя ошибка прогнозов нормированных значений (0,5%) была достигнута при ошибке на тестовой выборке (0,7%) при следующих условиях: два скрытых слоя по 5 и 1 нейрону соответственно (рис.3); 1121 эпоха обучения сети; активационная функция – гиперболический тангенс; функция ошибок задана через сумму квадратов ошибок; исключена активационная функция при переходе к выходному слою нейронов. Остальные параметры оказывали незначительное воздействие на процесс обучения.
Для построенной нейросетевой модели Web–Inf опасность недообучения нейросети практически исключена в силу малого числа входных переменных (5 показателей). Чтобы избежать опасности переобучения нами использовался рассмотренный выше двойной фильтр на точность.
Для понимания степени успешности модели Web–Inf необходимо сравнить качество тестовых прогнозов темпов инфляции, полученных на основе эконометрической модели (2) и модели Web–Inf. Как видно из табл.4, преимущество нейросети по критерию точности прогноза является тотальным. Тем самым второй шаг в построении модели инфляции путем калибровки «первичной» эконометрической зависимости (2) посредством вторичной нейросетевой модели себя полностью оправдал.
Таблица 4
Тестовые прогнозы темпов инфляции по моделям (2) и Web–Inf
|
Прогнозный период |
Фактический темп инфляции |
Прогноз темпов инфляции |
|
|
по модели (2) |
по модели Web–Inf |
||
|
Ноябрь 2017 |
0,22 |
0,1567 |
0,2269 |
|
Декабрь 2017 |
0,42 |
0,3174 |
0,4265 |
|
Январь 2018 |
0,31 |
0,0065 |
0,3141 |
|
Средняя ошибка аппроксимации прогноза, % |
– |
50,4 |
2,0 |
Подчеркнем, что само сравнение точности прогнозов по двум моделям призвано показать не прогностический потенциал нейросети самой по себе, а ее возможности по повышению предикативных свойств первичной эконометрической модели (2). При этом хорошие статистические параметры регрессионной модели (2), как правило, гарантируют весьма точные прогнозы по модели Web–Inf, в то время как применительно к нейросетевым моделям, построенным в автономном режиме (без предварительного отбора объясняющих переменных с помощью модели (2)), такой гарантии нет из-за риска ее переобучения.
Учитывая, что двухшаговая процедура прогнозирования представляет собой последовательное сочленение эконометрической и нейросетевой моделей, искомую гибридную модель будем обозначать Eco–Web.
Обсуждение результатов. Усложнение в последние десятилетия феномена инфляции и представление его в виде комбинации нефиксированного набора большого числа переменных разной природы привело к тому, что его прогнозирование с помощью традиционных моделей себя уже не оправдывает. Выход из создавшегося положения видится в построении более сложного алгоритма прогнозирования с аналитическим ядром в виде гибридной модели, представляющей собой смесь эконометрического и нейросетевого инструментариев. Такой вычислительный комплекс обладает большей гибкостью при учете краткосрочных флуктуаций, сохраняя при этом относительную простоту. Апробация гибридной модели Eco-Web показала ее работоспособность на коротких (2–3 месяца) горизонтах прогнозирования, однако попытки пролонгировать прогнозный период еще на несколько месяцев не дают положительных результатов. Тем самым даже гибридные модели обладают строго ограниченными прогностическими возможностями.
Вместе с тем схема гибридных моделей предполагает развитие в разных направлениях. Например, первичный отбор значимых переменных можно осуществлять не на базе корреляционной матрицы ИПЦ, а с помощью первичной нейросетевой модели. Тем самым использованная в данной работе схема сопряжения «эконометрическая модель – нейронная сеть» может преобразовываться в более сложную цепочку «нейронная сеть – эконометрическая модель – нейронная сеть». Можно дополнить гибридную модель аналитическим интерфейсом, направленным на идентификацию пороговых событий, сигнализирующих о необходимости пересмотра набора объясняющих переменных и спецификации модели [2]. По всей видимости, обеспечение адекватности модельных прогнозов инфляции возможно только за счет дальнейшего усложнения всей аналитической конструкции прикладных расчетов.
Литература
1. Балацкий Е.В., Юревич М.А. Использование нейронных сетей для прогнозирования инфляции: новые возможности // Вестник УрФУ. Серия Экономика. 2018. Том 17, № 5. С. 823–838, DOI: 10.15826/vestnik.2018.17.5.037.
2. Балацкий Е.В., Екимова Н.А. Учет пороговых немонетарных событий в гибридных моделях инфляции // Вопросы регулирования экономики. 2019. Том 10, №1.
3. Bates J.M. and Granger C.W.J. The Combination of Forecasts // Journal of the Operational Research Society. 1969. Vol. 20, no. 4. Pp. 451–468.
4. Newbold P. and Granger C.W.J. Experience with Forecasting Univariate Time Series and Combination of Forecasts // Journal of Royal Statistical Society. 1974. Vol. 137, no. 2. Pp. 131–164.
5. Балацкий Е.В., Юревич М.А. Прогнозирование инфляции: практика использования синтетических процедур // Мир новой экономики. 2018. Т. 12, № 4. С. 20–31.
6. Васильев А.А. Генезис гибридных моделей прогнозирования на основе объединения прогнозов // Вестник Тверского государственного университета. Серия: Экономика и управление. 2014. № 1. C. 316–331.
7. Zhang P.G. Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model // Neurocomputing. 2003. Vol. 50, no. 17. Pp. 159–175.
8. Tian F.P. and Ma L.L. Forecast of Cerebral Infraction Incidence Rate Based on BP Neural Network and ARIMA Combined Model / In International Symposium on Intelligence Information Processing and Trusted Computing. Chine, 2010. Pp. 216–219, DOI: 10.1109/iptc.2010.7.
9. Wang B., Hao W.N., Chen G., He D.C. and Feng B.A. Wavelet Neural Network Forecasting Model Based on ARIMA // Applied Mechanics and Materials. 2013. Vol. 347-350. Pp. 3013–3018.
10. Bozkurt O.O., Biricik G. and Taysi Z.C. Artificial neural network and SARIMA based models for power load forecasting in Turkish electricity market // PLOS ONE. 2017. No. 12(4). DOI: 10.1371/journal.pone.0175915.
11. Xuemei L.A, Lixing D., Ming S., Gang X. and Jibin L. Novel Air–conditioning Load Prediction Based on ARIMA and BPNN Model / In Asia–Pacific Conference on Information Processing. Chine, 2009. Pp. 51–54, DOI: 10.1109/apcip.2009.21.
12. Моисеев С.Р. Правила денежно–кредитной политики // Финансы и кредит. 2002. № 16. С. 37–46.
13. Екимова Н.А. Институциональные риски: в поисках детерминант инфляции // Вестник УрФУ. Серия экономика и управление. 2018. Т. 17, №5. С. 732–750.
14. Hnatkovskay V., Lahiriy A., Veghz C. The Exchange Rate Response Puzzle. 2012. [Электронный ресурс]. Режим доступа: https://ssrn.com/abstract=1996693
15. Cochrane J. Do Higher Interest Rates Raise or Lower Inflation? 2016. [Электронный ресурс]. Режим доступа:
https://www.newyorkfed.org/medialibrary/media/research/conference/2016/woodford/cochrane_dohigherinterestratesraiseorlowerin
flation
16. Cochrane J. The Grumpy Economist. 2015. [Электронный ресурс]. Режим доступа: https://johnhcochrane.blogspot.com/2015/11/early-fisherism.html
17. Горшкова Т., Синельникова Е. Сравнительный анализ прогнозных свойств моделей российской инфляции // Научный вестник ИЭП им. Гайдара. 2016. №6. С. 34–41.
[1] В целях улучшения модели (1) осуществлялся учет сезонной компоненты в полученном уравнении регрессии путем введения фиктивных переменных для каждого из месяцев года. Оценка модели с dunny–переменными показала, что существует статистически значимая связь между зависимым регрессором и некоторыми сезонными факторами. Однако в такой конфигурации значимость теряли основные объясняющие переменные, что приводило к потере качества всей модели. Аналогичные последствия возникали при имплементации в уравнение регрессии авторегрессионных компонентов. По всей видимости, колебания ИПЦ могут быть полностью объяснены (до определенного уровня точности) значениями этого показателя в предыдущих периодах (что, кстати, подтверждается многочисленными успешными моделями ARIMA, построенными для России и других стран). Вместе с тем, введение монетарных и немонетарных факторов в модель приводит к разрушению установленных взаимосвязей.
[2] Заметим, что коэффициент Дарбина–Уотсона в моделях (1) и (2) не проходят тест на отсутствие автокорреляции, однако для использования модели в качестве точки отсчета для дальнейшей работы с нейронной сетью данное обстоятельство не имеет значения; прогнозирование по моделям (1) и (2) не ведется, в связи с чем тест на наличие автокорреляции не имеет критического значения.
[3] Интегральный показатель влияния немонетарных факторов инфляции представляет собой среднее значение количественной и качественной меры влияния данной группы факторов [2].
Официальная ссылка на статью:
Балацкий Е.В., Екимова Н.А., Юревич М.А. Краткосрочное прогнозирование инфляции на основе маркерных моделей // «Проблемы прогнозирования», №5, 2019. С. 28–40.