1. Введение

Уровень цен считается одним из ключевых показателей состояния экономики, а его прогнозирование – важнейшей задачей центральных банков и аналитических компаний. В этой области мировая научная мысль накопила существенный опыт, позволяющий применять широкий набор инструментов для предсказания динамики цен на краткосрочный, среднесрочный и долгосрочный периоды. Существует не только множество конкурирующих формализованных моделей и вычислительных приемов, но и почти безграничный перечень индикаторов, продемонстрировавших свои предиктивные свойства по отношению к инфляции. Однозначное выдвижение лучшего способа прогнозирования динамики уровня цен едва ли осуществимо в силу того, что все модели в той или иной степени применимы к определенному состоянию или типу экономики и к ограниченному временному интервалу. Между тем появление так называемых «черных лебедей» подрывает надежность, казалось бы, непревзойденных в плане объяснения и предсказания моделей, открывая возможности для разработки альтернативных подходов с учетом появления новых аналитических инструментов.

Цель данной статьи состоит в рассмотрении возможностей наиболее популярных инструментов прогнозирования инфляции, выяснении их сравнительных недостатков и преимуществ, а также в выявлении нового тренда в использовании накопленного разнообразия методов предсказания будущих изменений цен. Кроме того, в статье будет в общих контурах сконструирована наиболее плодотворная синтетическая схема осуществления прикладных краткосрочных прогнозов инфляции.

2. Типология инструментов прогнозирования инфляции

Все многообразие подходов прогнозирования динамики уровня цен можно условно разделить на три обособленные группы: опросы; математические методы; моделирование с учетом экспертных оценок.

Систематические исследования инфляционных ожиданий стали проводится в 70-х годах ХХ в. и включали в себя как опросы ученых и специалистов в области функционирования экономики (например, в США Опрос профессиональных прогнозистов (Survey of Professional Forecasters) или Экономчиеские показатели Blue Chip (Blue Chip Economic Indicators)), так и обследования мнений рядовых субъектов экономической деятельности (ежемесячный опрос Университета Мичигана (University of Michigan: Inflation Expectation)) [1].

Вторую группу методов составляют математические модели, которые в свою очередь также подразделяются на две суб–группы: однофакторные и многофакторные. В первом случае помимо «трендирования» показателей инфляции (дефлятор ВВП, ИПЦ или т.д.) часто используется процедура Бокса–Дженкинса (интегрированная модель авторегрессии – скользящего среднего (ARIMA)), имеющая широкий функционал по учету лагированных значений оцениваемой величины. Многофакторные модели прогнозирования инфляции наравне с моделями, содержащими качественные переменные или экспертно устанавливаемые коэффициенты влияния, стали активно разрабатываться в конце 60-х – начале 70-х годов прошлого столетия [2]. Именно в рамках этих моделей было накоплено наибольшее количество различных приемов и технических инструментов построения прогнозов инфляции. К настоящему времени насчитывается порядка 20 типов таких моделей [3], среди которых выделяются:

– модели на основе Кривой Филлипса;

– векторные авторегрессионные модели (VAR);

– динамические модели общего равновесия (DSGE);

– нейронные сети.

Появление множества суб–классов моделей прогнозирования инфляции в основном связано с применением ряда типовых математических приемов, повышающих точность предсказаний. К их числу относится использование показателя «разрыва» (gap) инфляции, который демонстрирует разницу между равновесным и фактическим значением уровня цен. Этот прием получил особую популярность в рамках авторегрессионных моделей и моделей на основе кривой Филлипса [3]. Другим примером усиления предиктивной способности стандартных моделей выступает их калибровка на больших данных или объединение прогнозов, полученных различными способами. Вторая задача решается, в частности, при помощи равновзвешенного усреднения (Equal–weighted averaging), вычисления весов частных прогнозов исходя из параметров качества моделей (например, среднеквадратичная ошибка прогноза (RMSPE)) или методом баейсовского усреднения моделей, позволяющим отсеивать статистически значимые объясняющие переменные исходя из оценки большого числа спецификаций модели [4].

Что касается практического применения всего множества моделей, то здесь уже сформировалась генеральная линия, предполагающая использование процедур синтеза частных прогнозов, сделанных на базе моделей разного класса и типа. Например, центральные банки почти всех стран используют комбинацию различных инструментальных подходов (табл.1), включая экспертные, после чего все прогнозы усредняются по одной из указанных выше схем.

Ниже мы более подробно рассмотрим недостатки и преимущества наиболее популярных классов моделей прогнозирования инфляции.

Таблица 1. Базовые модели анализа экономики, применяемые центральными банками.

Tabl. 1. Central banks’ basic models of economy analysis.

Источник: составлено по [5–8]

3. Однофакторные модели прогнозирования инфляции

Подобные модели демонстрируют свою пригодность в основном на краткосрочном временном интервале. Их главными достоинствами являются простота применения и легкость интерпретации полученных зависимостей. В качестве независимой переменной нередко используется уровень инфляции в предыдущих периодах, однако и другие регрессоры также отлично вписываются в такого рода модели (например, модель, основанная на канонической кривой Филлипса). К типовым однофакторным моделям относится целый ряд популярных моделей.

1. Модели случайного блуждания (RW). RW–модели широко распространены в разных научных областях, позволяя анализировать нестационарные процессы, лишенные цикличности или трендовой составляющей. При анализе инфляции зачастую используется вариация, предложенная Аткесоном и Оханианом [9]:

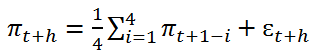                                                                                  (1)

где π_t – величина инфляции в период t; h – горизонт планирования; ɛ_t+h – случайная ошибка.

2. Модели прямой авторегрессии (DAR). Данные модели выглядят следующим образом:

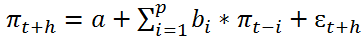                                                                           (2)

где π_t – величина инфляции в период t; α, b – коэффициенты при переменных; h – горизонт планирования; ɛ_t+h – случайная ошибка.

3. Модели рекурсивной авторегрессии (RAR). Модели этого типа имеют вид:

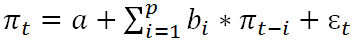                                                                                  (3)

где π_t – величина инфляции в период t; α, b – коэффициенты при переменных; ɛ_t – случайная ошибка.

Горизонт планирования, превышающий один временной интервал, достигается путем поэтапного проведения итераций с шагом в один период. Следует отметить, что модели DAR и RAR крайне редко используются в последние годы как в исследовательской, так и в практической сфере.

4. Модели стохастической волатильности с ненаблюдаемой составляющей (UCSV). UCSV–модели имеют некоторое сходство с моделями случайного блуждания, но добавление случайной ненаблюдаемой переменной позволяет моделировать необъяснимые рыночные шоки. Высокие прогностические свойства подобной модели были, в частности, продемонстрированы на примере США [10].

5. Интегрированные модели авторегрессии – скользящего среднего (ARIMA). Модель ARIMA (p,d,q) имеет вид:

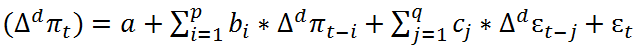                                          (4)

где p – порядок авторегрессии; q – порядок скользящего среднего; d – порядок разности; π_t – величина инфляции в период t; α, b, c – коэффициенты при переменных; ɛ_t – случайная ошибка.

Модели ARIMA широко применяются в экономическом анализе, в том числе и для прогнозирования инфляции. В частности, с конца 2003 г. сотрудниками Института экономической политики им. Е.Т.Гайдара раз в месяц публикуются прогнозы около 50 российских макроэкономических показателей, получаемые при помощи модели ARIMA [8].

4. Модели на основе кривой Филлипса

Идея о связи между инфляцией и уровнем безработицы была высказана Филлипсом еще в 1957 г. Спустя десятилетие Фридман и Фелпс обнаружили, что в долгосрочном периоде эта взаимосвязь нестабильна, т.к. экономические агенты обладают инфляционными ожиданиями, которые и оказывают решающие воздействие на процесс принятия решений. С учетом этой критики была разработана так называемая «треугольная модель» [11], в которой темпы инфляции задаются тремя переменными: уровнем безработицы, шоками издержек и прошлыми значениями инфляции.

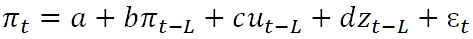                                                                 (5)

где π_t – величина инфляции в период t; α, b, c, d – коэффициенты при переменных; u_t – уровень безработицы; z_t – переменная, характеризующая шок предложения; L – величина лага; ɛ_t – случайная ошибка.

Модель успешно прошла апробацию на данных США – инфляция была выражена динамикой цен на продовольственные продукты и энергоресурсы, а шоки издержек представлялись в виде динамики средних импортных цен [12]. Кроме того, в модель были введены фиктивные переменные, характеризующие меры государственной политики по регулированию уровня заработных плат.

Другим направлением доработки кривой Филлипса является введение предпосылки о некотором постоянном уровне безработицы, которая не ускоряет инфляцию (NAIRU). Как следует из названия концепции, при отклонении от равновесного или естественного уровня безработицы инфляция либо ускоряется, либо замедляется. Главной проблемой является определение этого естественного уровня и его изменений в долгосрочном периоде. До 1990-х гг. модель NAIRU пользовалась большим спросом, но для США стали проявляться демографические и технологические шоки, не позволяющие эффективно применять эту концепцию без существенных математических доработок [13].

В рамках новой кейнсианской модели экономики кривая Филлипса была дополнена отклонением средних предельных издержек производства от их равновесного уровня. Это нововведение строилось на гипотезе о большой рыночной власти фирм–монополистов, которые скорее не воспринимают изменения уровня цен как нечто заданное, а выступают агентами, непосредственно устанавливающими эти цены [14].

Еще одним дополнительным фактором, повысившим предиктивную точность моделей на основе кривой Филлипса, стал способ «открытия» экономики. Так, инфляция помимо всех указанных ранее переменных объяснялась еще и динамикой обменного курса валют, инфляцией в странах–партнерах в сфере торговли и другими параметрами [15]. В частности, подобная модель была построена для Великобритания, что позволило установить равнозначный вклад в формирование будущих значений инфляции факторов безработицы и средних импортных цен, которые преимущественно зависели от реальных мировых цен на нефть [16]. Для стран Еврозоны (в целом и отдельно для 9 государств) модель с «открытой» экономикой, выраженной стоимостью импортных промежуточных товаров, оказалась точнее по сравнению с ее стандартной спецификацией [17].

Что касается применения кривой Филлипса для моделирования инфляционных процессов в России, то отечественным экономистам также удалось накопить существенный опыт в этом вопросе. И хотя в ряде работ [например, 18,19], посвященных обнаружению отрицательной зависимости инфляции от безработицы в 1990-х и 2000-х гг., были получены выводы о ценообразовании в России, отрицающие гипотезу Филлипса и его последователей, в дальнейших исследованиях искомую связь все-таки удалось идентифицировать. Так, была обнаружена статистически значимая зависимость индекса потребительских цен (ИПЦ) от уровня безработицы, инфляционных ожиданий, цены на нефть и обменного курса рубля для 2003–2007 гг. [20]. Более того, по месячным данным за период с 1999 по 2013 гг. была обнаружена зависимость текущего значения ИПЦ как от прошлых значений, так и от будущих, т.е. от инфляционных ожиданий. В данной модели вместо безработицы был использован «разрыв» ВВП [21], что соответствует зарубежной практике. Нельзя не отметить и тот факт, что в данных работах цель построения прогнозов инфляции в России как таковая не ставилась, т.к. акцент делался именно на обнаружение традиционных взаимосвязей, однако включение в модель лагированных значений переменных автоматически открывает широкие прогностические возможности построенных моделей.

В последние десятилетия связь между инфляцией и безработицей все активнее ставится под вопрос. С одной стороны, утверждается, что возросшая конкуренция, в том числе глобальная, не позволяет фирмам повышать цены, а работникам требовать более высоких заработных плат в ответ на рост внутреннего спроса. С другой стороны, центральные банки существенно расширили свои возможности по управлению инфляцией, манипулируя инфляционными ожиданиями населения и компаний, что привело к меньшей чувствительности среднего уровня цен в экономике к колебаниям рыночной конъюнктуры [22]. Тем не менее, несмотря на обширную критику кривой Филлипса, данная концепция с существенными модификациями по-прежнему активно применяется при моделировании инфляционных процессов, хотя на уровне поддержки принятия управленческих решений уже не столь широко.

5. Векторные авторегрессионные модели

Модели векторной авторегрессии стали доминирующими в эмпирическом анализе монетарной политики, начиная с работы Симса [23] 1992 г., в которой экономика была представлена в виде системы одновременных уравнений. В исследуемую выборку было включено 5 стран (США, Великобритания, Германия, Франция и Япония) и 6 переменных (процентная ставка, денежный агрегат М1, ИПЦ, индекс промышленного производства, обменный курс национальной валюты и индекс оптовых цен). В общем виде модели VAR записываются:

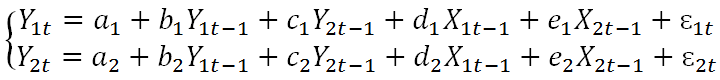                                   (6)

где Y_1t, Y_2t – эндогенные переменные; Х_1t, Х_2t – экзогенные переменные; α, b, c, d, e – коэффициенты при переменных; ɛ_1t, ɛ_2t – случайные ошибки.

Один из главных выводов, полученных на основе приведенной модели, заключается в постоянном и стремительном увеличении уровня цен в экономике при повышении процентной ставки (т.е. из-за шока со стороны монетарной политики). Это явление получило название «парадокс цен» и самим Симсом объяснялось присутствием некоторого скрытого эндогенного фактора, выражающегося в изменении ставки процента как реакции регулятора на экономическую ситуацию.

Другим известным идеологом VAR–моделей прогнозирования инфляции является экс-глава ФРС США Б.Бернанке. Им была предложена факторно–расширенная модель векторной авторегрессии (FAVAR) [24], позволяющая учитывать динамику не только основных переменных, но и их главных компонент. Это нововведение позволило нивелировать эффект «парадокса цен», поскольку компоненты, состоящие из линейной комбинации объясняющих переменных, имеют возможность фиксировать импульсные отклики на шоки любой переменной, входящей в состав фактора. Также метод главных компонент позволил рассмотреть порядка 120 переменных, объединенных в группы: выпуск и доход; занятость; потребление; разрешения на строительство и продажу недвижимости; запасы и ордеры (заказы); фондовые индексы; обменные курсы; процентные ставки; денежные и кредитные агрегаты; индексы цен; средняя заработная плата.

Свое дальнейшее развитие векторные авторегрессионные модели получили в виде увеличения масштаба анализа – путем перехода к глобальным VAR–моделям (GVAR). Такие модели строятся в два этапа: во-первых, определяются зависимости между переменными в рамках каждой из обследуемых стран; во-вторых, объединяются страновые VAR–модели в единую систему с учетом взаимного влияния каждой из стран. Этот прием был использован, в частности, для стран Еврозоны [25]. Одним из непосредственных результатов такого подхода стало доказательство реакции уровня цен в европейских странах на шоки монетарной политики в США.

Основной сферой применения VAR–моделей и их спецификаций (к примеру, для больших данных – байесовская дополненная факторами векторная авторегрессия (BFAVAR)) стало моделирование действий центральных банков для вычисления реакции на них основных экономических индикаторов. В частности, имитация «шоков» выступала важным подспорьем для принятия решения об изменения ключевой ставки или ее аналогов. В то же время, VAR–модели позволили обнаружить ряд парадоксов, которые были разрешены в процессе эволюции и усложнения самих моделей. Так, упомянутый «парадокс цен» был обнаружен в России при использовании стандартной модели векторной авторегрессии, но применение метода главных компонент эту гипотезу опровергло [26].

Преимуществом и одновременно недостатком VAR-моделей принято считать отсутствие каких-либо ограничений со стороны экономической теории в части взаимозависимостей переменных [27]. С практической точки зрения высокий уровень точности прогнозирования, очевидно, куда более важен по сравнению с беспрекословным соблюдением догматов экономической теории, что и объясняет высокую востребованность VAR–моделей, особенно в байесовской спецификации, среди сотрудников органов государственного регулирования.

6. Динамические модели общего равновесия

С точки зрения учета максимально возможного числа объясняющих переменных динамические модели общего равновесия (DSGE) не имеют себе равных. Обратной стороной медали является высокая сложность их построения из-за трудоемкости сбора исходных данных и определения систем взаимосвязи используемых индикаторов. Вместе с тем результатами симуляций становятся прогнозы не одной–единственной переменной, а всей моделируемой экономики.

Среди первых попыток описания «малых» экономик при помощи DSGE–моделей выделяются работы Фюрера [28] и Дель Негро совместно с Шорфайдом [29]. В обоих исследованиях фигурировали всего три наблюдаемых переменных: совокупный выпуск, уровень инфляции и ставка процента.

Прорывные DSGE–модели «средних» экономик, включающие уровень цен, были представлены в работах Сметса и Воутерса [30,31]. В их более ранней статье была смоделирована экономика Еврозоны с учетом экономической деятельности домохозяйств, фирм и влияния технологий. Помимо среднего уровня цен в качестве эндогенных переменных экономики фигурировали: совокупный выпуск, объемы потребления и инвестиций, уровень заработной платы, фонд рабочего времени и ставка процента. В сравнении с VAR-моделями DSGE–модель показала высокую точность. В исследовании, посвященному американской экономике, использовался почти идентичный подход за исключением нескольких технических изменений. Полученные результаты также продемонстрировали превосходство DSGE–модели над разновидностями VAR–моделей.

DSGE-модель «большой» экономики была создана сотрудниками Федеральной резервной системы США [32]. Усложнение модели выразилось в разделении совокупного потребления на потребление товаров кратковременного использования и услуг и потребление товаров длительного пользования; инфляции – по той же схеме; совокупных инвестиций – на инвестиции домохозяйств и бизнеса. Как было показано в работе, увеличение числа наблюдаемых переменных способствовало росту точности прогнозирования всей моделируемой системы.

Любопытные оценки качества упомянутых DSGE–моделей были получены при сопоставлении их точности прогнозирования не только с VAR–моделями, но и с экспертными оценками [33]. Если VAR–модели проигрывали как каждой из DSGE–моделей в отдельности, так и усредненному прогнозу, то прогнозы, опубликованные в Зеленой книге ФРС США, также оказались ближе к реальным значениям.

Дальнейшее развитие DSGE–моделей происходило в русле их усложнения, т.е. добавления наблюдаемых переменных, «открытия» экономики, внедрения более изощренных математических приемов описания связей между параметрами. Модели такого класса уже стоят на вооружении центральных банков в разных странах помимо США (например, в Европейском центральном банке, центральных банках Канады, Швеции, Чехии, Швейцарии, а также в Международном валютном фонде) [34] и выступают в качестве рабочего инструмента прогнозирования динамики уровня цен. Вместе с тем динамические модели общего равновесия подвергаются серьезной критике, которая, в конченом счете, сводится к неспособности предсказания финансовых кризисов.

7. Нейронные сети

Нелинейность взаимосвязей между зависимыми и независимыми переменными не позволяет определить оптимальную форму модели. В последние годы эти проблемы стали решаться путем построения искусственных нейронных сетей, которые хоть и не имеют четкой аналитической формы, но характеризуются более точными предикативными возможностями.

Одной из первых работ в этой области стало прогнозирование месячных цен на живой скот и пшеницу в 1995 г. [35]. Индекс потребительских цен предсказывался в США в 1999 г. [36] – нейросеть оказалась точнее регрессионных моделей. Превосходство нейронный сетей над моделями ARIMA и VAR было продемонстрировано на примере инфляции в Еврозоне [37]. Исследования в данной сфере охватили как инфляцию в глобальной экономике (например, прогноз инфляции в странах ОЭСР [38]), так и флуктуации уровня цен в отдельных странах (Индия [39], Пакистан [40], Турция [41] и др.).

Отечественная научная мысль также не осталась в стороне от нового начинания. В 2005 г. было опубликовано исследование, посвященное построению нейросети месячной инфляции в РФ за 2003–2004 гг. [42]. В качестве зависимых переменных рассматривались ИПЦ на продовольственные товары, ИПЦ на непродовольственные товары и ИПЦ на потребительские услуги, а в качестве объясняющей – индекс цен производителей с лагами от 0 до 12 месяцев. Более широкий период (с 1991 по 2008 гг.) динамики инфляции в России был интегрирован в нейронную сеть с предпосылкой о зависимости текущего значения уровня цен от аналогичного показателя в каждом из предшествующих 12 месяцев [43]. Приемлемые ошибки получились при построении сетей для отдельных периодов, которые авторы работы классифицировали как «интервалы действия определенных экономических тенденций». Достаточно точные прогнозы помесячного изменения ИПЦ были достигнуты при учете более широкого перечня факторов: индексов цен производителей различных групп товаров, индекса тарифов на грузовые перевозки, сводного индекса цен строительной продукции, ВВП и денежной массы (периода анализа: с 2000 по 2010 г.) [44]. Уровень безработицы и валютный курс также оказались качественными предикторами инфляции в России [45]: модель, основанная на учете только прошлых значений уровня инфляции, дала менее адекватные результаты. Кроме того, в рамках указанной работы поквартальное прогнозирование изменения уровня цен дало более точные результаты по сравнению с прогнозными расчетами месячных колебаний.

Модели прогнозирования инфляции на основе искусственных нейронных сетей в подавляющем большинстве исследований оцениваются с точки зрения точности самих прогнозов и в сравнении с регрессионными моделями. К сожалению, высокой точности предсказания месячной инфляции добиться почти не удается, зато превосходство над регрессионными моделями, которые также не преуспели в этом деле, демонстрируется в краткосрочном и особенно в долгосрочном периодах. Хотя нейросети пока не стали надежным и широко распространенным инструментом прогнозирования инфляции и поддержки принятия мер монетарной политики, но потенциал у этого направления крайне высок.

8. Сравнительные характеристики качества моделей прогнозирования инфляции

В современных разработках одним в качестве основного критерия качества предлагаемых подходов используется более высокая точность по сравнению с разработанными ранее моделями. Причем иногда авторы используют уже готовую конфигурацию и расчетные оценки, а иногда – применяют «чужую» модель на собственной выборке. Итогом такой процедуры становится демонстрация превосходства авторской разработки над целым набором альтернативных подходов, причем зачастую с огромным отрывом. Однако в этом приеме скрыто определенное лукавство. Дело в том, что новые модели, выбираемые для сравнения, служат эталоном для разрабатываемого подхода, т.е. новая модель улучшается до тех пор, пока не превзойдет предыдущие. На этом фоне калибровка новых данных к уже известной схеме либо вообще не проводится, либо не отличается особым усердием. Таким образом, интерпретировать сравнительные преимущества предлагаемых моделей следует не в русле принципиальной смены парадигмы, а в более взвешенной конвенциональной формулировке: предложенная новая модель способна дать лучшие объясняющие или предиктивные свойства по сравнению с имеющимися аналогами на исследуемой выборке и при определенном наборе объясняющих переменных.

Однако в зарубежной научной литературе есть несколько работ, содержащих, по всей видимости, непредвзятое компаративное исследование различных моделей прогнозирования инфляции. Главное условие объективности – отсутствие собственной модели, достоинства которой раскрываются и доказываются по ходу изложения материала.

В настоящее время можно говорить о трех фундированных компаративных исследованиях, которые охватывают почти все разнообразие имеющегося модельного инструментария, включая экспертные оценки и статистические базы данных [3, 46, 47]. В табл.2 представлен набор моделей, попавших в зону сравнительного анализа (обозначены плюсом).

Таблица 2. Сравнение моделей прогнозирования инфляции.

Tabl. 2. Comparison of inflation forecasting models.

Источник: составлено по [3, 46, 47].

В работе Фауста и Райта 2009 г. ключевым выводом, полученным по итогам сопоставления моделей, стало превосходство экспертных оценок по сравнению со всеми моделями. Среди количественных методов большую точность продемонстрировали многофакторные модели. В связи с тем, что в статье рассматривались различные лаги для объясняющих регрессоров и различные горизонты планирования, то выделить одну или две лучшие модели проблематично, тем не менее, сами авторы отдают предпочтение байесовскому усреднению моделей и интегрированной факторно–расширенной модели векторной авторегрессии.

В более масштабном исследовании 2011 г. экспертные прогнозы вновь оказались самыми точными. Наименее адекватные прогнозы были получены по моделям прямой и рекурсивной авторегрессии, а также на основе кривой Филлипса. В рамках нескольких итераций методы усреднения моделей и VAR–модель оказались даже точнее экспертных данных. Кроме того, модель стохастической волатильности с ненаблюдаемой составляющей показала достойные результаты, если сравнивать ошибку по всем вариантам построения прогноза. DSGE–модель также получила достаточно высокую оценку, хотя точность прогноза, эквивалентная экспертному мнению, была достигнута только на одном горизонте планирования из шести смоделированных.

Экспертные оценки не были включены в перечень оцениваемых подходов прогнозирования инфляции в статье Дункана и Мартинеза–Гарсии, поскольку исследование было выполнено для 14 стран с развивающейся экономикой. По каждому из четырех протестированных горизонтов планирования наименьшую ошибку продемонстрировала модель случайного блуждания. Хотя по отдельным странам и с отдельно взятыми горизонтами планирования другие модели показывали лучше результаты (даже модели прямой авторегрессии), в целом же превосходство RW–модели получилось безоговорочным.

9. Заключение

Проведенное сравнение существующей практики прогнозирования инфляции позволяет сделать ряд принципиальных выводов.

Во-первых, деятельность по прогнозированию инфляции органично связана с процедурой выбора конкретного и наиболее подходящего инструментария. Накопленный к настоящему времени огромный арсенал методов и моделей предоставляет исследователю широкий набор альтернативных решений.

Во-вторых, сам акт выбора представляет собой нетривиальную процедуру, т.к. все преимущества имеющихся подходов имеют контекстный характер, т.е. принципиально зависят от количественной выборки, которая в свою очередь зависит от конкретного типа изучаемых стран, временных периодов анализа, наборов и спецификации переменных конструируемых моделей.

В-третьих, все современные прогнозы представляют собой агрегирование частных прогнозов, полученных с помощью разных инструментариев. Иными словами, вместо моно–прогнозов, основанных на применении одного подхода, формируются поли–прогнозы, учитывающие множество разных подходов. Такая практика связана с тем обстоятельством, что преимущества всех методов являются не абсолютными, а относительными (зависящими от конкретных статистических данных), в связи с чем и сами преимущества носят крайне неустойчивый характер. Попытки повысить устойчивость успеха подготавливаемых прогнозов требуют комбинирования и объединения потенциала разных инструментариев.

Последний указанный аспект требует особого комментария. Дело в том, что пока практика применения различных подходов осуществляется исключительно посредством применения «чистых» инструментальных подходов с последующим «сжатием» полученных прогнозных сценариев. Иными словами, разные способы моделирования осуществляются в автономном режиме, а дополнительная вычислительная процедура применяется уже только к подготовленным на их основе прогнозам. Вместе с тем во многом недоиспользованным остается потенциал построения «смешанных» моделей, когда разные виды прогнозного инструментария используются совместно, как правило, последовательно, на разных стадиях прогнозирования. Например, было бы целесообразно апробировать вариант моделирования, когда годовые темпы инфляции прогнозирутся с помощью DSGE–модели, а калибровка помесячного ИПЦ внутри года осуществляется с помощью VAR–модели. Авторами данной статьи был апробирован другой перспективный подход: построение многофакторной эконометрической модели инфляции на базе помесячной разбивки с последующей калибровкой прогнозных значений с помощью нейронной сети. При такой комбинации методов достигается двойной результат – обеспечивается теоретическая канва в понимании и объяснении явления на фоне требуемой высокой точности прогноза.

На наш взгляд, в ближайшее время можно ожидать прогнозирования инфляции, равно как и других экономических явлений, на основе синтетических модельных процедур – в рамках чистых либо смешанных модельных стратегий. Потенциал второго типа синтетического моделирования представляется наиболее перспективным.

Список источников

1. Lahiri K., Zhao Y. Determinants of consumer sentiment over business cycles: Evidence from the US surveys of consumers // Journal of Business Cycle Research. 2016. Vol. 12. №. 2. P. 187–215.

2. Behravesh N. Forecasting inflation: does the method make a difference // Business Review. 1976. Sep. P. 9–17.

3. Faust J., Wright J.H. Forecasting inflation // Handbook of economic forecasting. 2013. Vol. 2. P. 2–56.

4. Wright J.H. Forecasting US inflation by Bayesian model averaging // Journal of Forecasting. 2009. Vol. 28. №. 2. P. 131–144.

5. Dou W., Lo, A., Muley A., Uhlig H. Macroeconomic models for monetary policy: a critical review from a finance perspective. 2017. SSRN working paper. URL: https://ssrn.com/abstract=2899842.

6. Hjelm G. et al. Appropriate macroeconomic model support for the ministry of finance and the national institute of economic research: a pilot study. 2015. National Institute of Economic Research working paper. URL: https://ideas.repec.org/p/hhs/nierwp/0137.html.

7. Андреев А. Прогнозирование инфляции методом комбинирования прогнозов в Банке России // Банк России. Серия докладов об экономических исследованиях. 2016. №. 14. С. 2–11.

8. Турунцева М.Ю., Астафьева Е.В., Петренко В.Д. Прогнозирование инфляции: эмпирика и реальность // Экономика. Налоги. Право. 2014. №. 1. С. 53–57.

9. Atkeson A. et al. Are Phillips curves useful for forecasting inflation? // Federal Reserve bank of Minneapolis quarterly review. 2001. Vol. 25. №. 1. P. 2–11.

10. Stock J.H., Watson M.W. Why has US inflation become harder to forecast? // Journal of Money, Credit and banking. 2007. Vol. 39. P. 3–33.

11. Gordon R. Inflation, Flexible Exchange Rates, and the Natural Rate of Unemployment. In Workers, jobs and inflation. Ed. Baily M. Washington: Brookings, 1982. P. 88–152.

12. Gordon R. U.S. Inflation, labor’s share and the natural rate of unemployment. In Economics of Wage Determination. Ed. Konig H. 1990. Berlin: Srpinger–Verlag. 373 P.

13. Ball L., Mankiw N.G. The NAIRU in theory and practice // Journal of economic Perspectives. 2002. Vol. 16. №. 4. P. 115–136.

14. Calvo G.A. Staggered prices in a utility-maximizing framework // Journal of monetary Economics. 1983. Vol. 12. №. 3. P. 383–398.

15. Razin A., Yuen C.W. The ‘New Keynesian’Phillips curve: closed economy versus open economy // Economics Letters. 2002. Vol. 75. №. 1. P. 1–9.

16. Batini N., Jackson B., Nickell S. An open-economy new Keynesian Phillips curve for the UK // Journal of Monetary Economics. 2005. Vol. 52. №. 6. P. 1061–1071.

17. Rumler F. Estimates of the open economy new Keynesian Phillips curve for euro area countries // Open economies review. 2007. Vol. 18. №. 4. P. 427–451.

18. Мухин Д.А. Краткосрочная кривая Филлипса и инфляционные процессы в России // Экономика и математические методы. 2010. Т. 46. №. 2. С. 118–130.

19. Сергушкина Л., Кривая А. Филлипса в переходной экономике России // Научная сессия МИФИ: сборник научных трудов. 2006. Т. 6. С. 168–169.

20. Гафаров Б.Н. Кривая Филлипса и становление рынка труда в России // Экономический журнал Высшей школы экономики. 2011. Т. 15. №. 2. С. 155–176.

21. Соколова А.В. Инфляционные ожидания и кривая Филлипса: оценка на российских данных // Деньги и кредит. 2014. Т. 11. С. 61–67.

22. The Economist. The Phillips curve may be broken for good. 2017. URl: https://www.economist.com/graphic-detail/2017/11/01/the-phillips-curve-may-be-broken-for-good

23. Sims C.A. Interpreting the macroeconomic time series facts: The effects of monetary policy // European economic review. 1992. Т. 36. №. 5. С. 975–1000.

24. Bernanke B.S., Boivin J., Eliasz P. Measuring the effects of monetary policy: a factor-augmented vector autoregressive (FAVAR) approach // The Quarterly journal of economics. 2005. Vol. 120. №. 1. P. 387–422.

25. Dees S. et al. Exploring the international linkages of the euro area: a global VAR analysis // Journal of applied econometrics. 2007. Vol. 22. №. 1. P. 1–38.

26. Шестаков Д.Е. Канал издержек денежно-кредитной трансмиссии в российской экономике // Деньги и кредит. 2017. №. 9. С. 38–47.

27. Моисеев С.Р. Аналитика центральных банков: обзор эконометрических моделей // Финансы и кредит. 2000. №11. С. 119–124.

28. Fuhrer J.C. Inflation/output variance trade-offs and optimal monetary policy // Journal of Money, Credit, and Banking. 1997. P. 214–234.

29. Del Negro M., Schorfheide F. Priors from general equilibrium models for VARs // International Economic Review. 2004. Vol. 45. №. 2. P. 643–673.

30. Smets F., Wouters R. An estimated dynamic stochastic general equilibrium model of the euro area // Journal of the European economic association. 2003. Vol. 1. №. 5. P. 1123–1175.

31. Smets F., Wouters R. Shocks and frictions in US business cycles: A Bayesian DSGE approach // American economic review. 2007. Vol. 97. №. 3. P. 586–606.

32. Edge R.M., Kiley M.T., Laforte J.P. Natural rate measures in an estimated DSGE model of the US economy // Journal of Economic Dynamics and control. 2008. Vol. 32. №. 8. P. 2512–2535.

33. Wolters M.H. Evaluating point and density forecasts of DSGE models // Journal of Applied Econometrics. 2015. Vol. 30. №. 1. P. 74–96.

34. Christiano L.J., Eichenbaum M.S., Trabandt M. On DSGE models // Journal of Economic Perspectives. 2018. Vol. 32. № 3. P. 113–140.

35. Kohzadi N., Boyd M.S. Testing for chaos and nonlinear dynamics in cattle prices // Canadian Journal of Agricultural Economics. 1995. Vol. 43. №. 3. P. 475–484.

36. Aiken M. Using a neural network to forecast inflation // Industrial Management & Data Systems. 1999. Vol. 99. №. 7. P. 296–301.

37. Binner J.M. et al. A comparison of linear forecasting models and neural networks: an application to Euro inflation and Euro Divisia // Applied economics. 2005. Vol. 37. №. 6. P. 665–680.

38. Choudhary M.A., Haider A. Neural network models for inflation forecasting: an appraisal // Applied Economics. 2012. Vol. 44. №. 20. P. 2631–2635.

39. Thakur G.S.M., Bhattacharyya R., Mondal S.S. Artificial neural network based model for forecasting of inflation in India // Fuzzy Information and Engineering. 2016. Vol. 8. №. 1. P. 87–100.

40. Haider A., Hanif M.N. Inflation forecasting in Pakistan using artificial neural networks // Pakistan economic and social review. 2009. P. 123–138.

41. Catik A.N., Karaçuka M.A comparative analysis of alternative univariate time series models in forecasting Turkish inflation // Journal of Business Economics and Management. 2012. Vol. 13. №. 2. P. 275–293.

42. Зарова Е.В., Заров И.К. Нейронные сети как средство моделирования и прогнозирования инфляционных процессов // Вестник Самарского государственного технического университета. Серия Физико-математические науки. 2005. №. 34. С. 182–186.

43. Коваленко А.В., Уртенов М.Х. Нейросетевое моделирование инфляции в России // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2010. №. 61. С. 278 – 297.

44. Огородов А.П. Учет влияния ряда факторов при прогнозировании инфляционных процессов на базе нейронных сетей // Электроника и информационные технологии. 2011. №. 1. URL: fetmag.mrsu.ru/2011-1/pdf/Forecasting_Of_Inflationary.pdf.

45. Горшкова Т., Синельникова Е. Сравнительный анализ прогнозных свойств моделей российской инфляции //Научный вестник ИЭП им. Гайдара. 2016. №. 6. С. 34–41.

46. Faust J., Wright J.H. Comparing Greenbook and reduced form forecasts using a large realtime dataset //Journal of Business & Economic Statistics. 2009. Vol. 27. №. 4. P. 468–479.

47 .Duncan R., Martínez-García E. New Perspectives on Forecasting Inflation in Emerging Market Economies: An Empirical Assessment. 2018. Working paper. URL: https://www.dallasfed.org/~/media/documents/institute/wpapers/2018/0338.pdf.

Официальная ссылка на статью:

Балацкий Е.В., Юревич М.А. Прогнозирование инфляции: практика использования синтетических процедур// «Мир новой экономики», №4, 2018. С.20–31.