Одной из фундаментальных особенностей инновационных рынков является логистический закон их развития. Математически такой процесс описывается диффузионным дифференциальным уравнением и подлежит довольно простой проверке на практике. Вместе с тем данный подход в явном виде не учитывает фискальную среду, в которой действует инновационное предприятие, в то время как данный вопрос в ряде случаев оказывается решающим. Действительно, неблагоприятный налоговый климат может не только затормозить, но и полностью подавить начавшееся формирование инновационного рынка. Ниже рассмотрим возможность включения фискального фактора производства в схему развития инновационного рынка на базе диффузионной модели.
Прежде всего, выясним некоторые особенности классической диффузионной модели применительно к отдельной инновационной фирме, осуществляющей экспансию нового рынка:
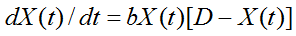 (1)
(1)
где X(t) – объем производства фирмы в момент времени t; D – потенциальный размер рынка, то есть спрос на продукцию фирмы; b – интенсивность осуществления фирмой экспансии нового рынка.
Главным и единственным параметром модели (1) является коэффициент b, который аккумулирует в себе все особенности моделируемого процесса. Так, в диффузионной модели не отражен в явной форме уровень прибыльности производства, который в частности зависит от уровня налоговой нагрузки. Не учтен в ней и факт сопротивления экономической среды экспансионистским действиям фирмы–инноватора и, в частности, со стороны ее конкурентов. Все это в агрегированной форме заложено в параметре b. Следовательно, модель (1) не позволяет изучать траектории развития фирмы в зависимости от регулирующих действий государства и, в частности, от устанавливаемого им уровня налоговой нагрузки. В связи с этим в дальнейшем наша задача будет состоять в «раскрытии» базовой модели (1) с учетом фискального фактора воспроизводственного цикла инновационного предприятия.
Для этого преобразуем уравнение (1) к модели следующего вида:
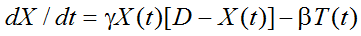 (2)
(2)
где T(t) – объем изымаемых с фирмы налогов в момент времени t; γ – параметр, характеризующий соответствующий товарный рынок; β – параметр, показывающий силу влияния и значимость налогового фактора на развитие предприятия. В соответствии с логикой модели выполняются условия: γ>0 и β>0.
Если предположить, что налоговое давление пропорционально объему производства фирмы, что наблюдается в реальности, и постоянно во времени, что также в целом не противоречит наблюдениям, то модель (2) примет окончательный вид:
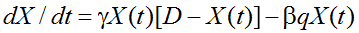 (3)
(3)
где q=T(t)/X(t) – доля налогов в объеме реализации (добавленной стоимости) предприятия.
Тогда решением дифференциального уравнения (3) будет логистическая функция следующего вида:
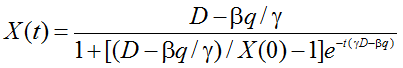 (4)
(4)
где X(0) – объем производства (реализации) предприятия в начальный период времени (через этот параметр фиксируются начальные условия).
Учитывая введенные обозначения, траектория налоговых сборов будет определяться по формуле:
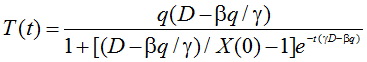 (5)
(5)
Полученные выражения (4) и (5) позволяют сделать целый ряд важных выводов.
Во-первых, влияние налоговой нагрузки q носит комплексный характер. Это непосредственно вытекает из того, то данный параметр участвует в формировании как предела производства (асимптоты) 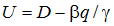 , так и динамических свойств рынка, входя под знак экспоненты. Кроме того, налоговый параметр входит в коэффициент при экспоненте, участвуя в формировании начальных условий. Следовательно, фискальный фактор пронизывает все стороны производства инновационной фирмы.
, так и динамических свойств рынка, входя под знак экспоненты. Кроме того, налоговый параметр входит в коэффициент при экспоненте, участвуя в формировании начальных условий. Следовательно, фискальный фактор пронизывает все стороны производства инновационной фирмы.
Во-вторых, налоги замедляют рост производства инновационного продукта. Это следует из анализа знака выражения под экспонентой.
В-третьих, рост налогов понижает производственную асимптоту, что эквивалентно факту сокращения потенциального спроса на инновационном рынке. Геометрически это означает, что асимптота–прямая под воздействием растущих налогов дрейфует вниз вплоть до приятия отрицательного значения, что означает полное разрушение инновационного рынка (предприятия). Таким образом, слишком высокие налоги могут полностью «раздавить» формирующийся сегмент инновационного рынка. Фискальная нагрузка q**, при которой U=0 и инновационный рынок «захлопывается» определяется по формуле: 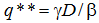 .
.
Надо сказать, что полученный вывод является довольно неожиданным, так как на первый взгляд кажется, что на предел производства налоги воздействовать не должны, ибо этот предел является внешним фактором по отношению к фирме–инноватору. Таким образом, налоги воздействуют не только на само предприятие, но и на инновационный рынок в целом, урезая совокупный спрос на нем.
Следует заметить, что влияние налогов на производственный предел U является линейным и не предполагает сложных эффектов. Иным образом обстоит дело с объемом фискальных сборов, для которых величина фискального предела (асимптоты) определяется квадратичной функцией q: 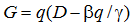 .
.
Данная формула позволяет сделать еще один вывод: налоговое бремя q нелинейно воздействует на предельную величину изымаемых налогов G и предполагает точку максимума q*:
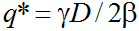 (6)
(6)
Учитывая, что 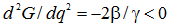 , стационарная точка (6) действительно является точкой максимума. Следовательно, эта величина должна восприниматься в качестве некоего разумного предела, превышение которого не только замедляет развитие инновационного предприятия и инновационного рынка, но и уменьшает собираемость налогов. В соответствии со сложившейся терминологией [1] существование точки (6) эквивалентно существованию точки А.Лаффера 2-го рода; точка А.Лаффера 1-го рода для случая инновационного сектора отсутствует. Разумеется, здесь речь идет лишь об определенной аналогии с традиционными лафферовыми эффектами, так как в чистом виде анализ провести невозможно из-за искажающего влияния временного фактора. Попутно заметим, что точка q* предъявляет более жесткие требования к настройке налоговой системы по сравнению с точкой q** (q**=2q*).
, стационарная точка (6) действительно является точкой максимума. Следовательно, эта величина должна восприниматься в качестве некоего разумного предела, превышение которого не только замедляет развитие инновационного предприятия и инновационного рынка, но и уменьшает собираемость налогов. В соответствии со сложившейся терминологией [1] существование точки (6) эквивалентно существованию точки А.Лаффера 2-го рода; точка А.Лаффера 1-го рода для случая инновационного сектора отсутствует. Разумеется, здесь речь идет лишь об определенной аналогии с традиционными лафферовыми эффектами, так как в чистом виде анализ провести невозможно из-за искажающего влияния временного фактора. Попутно заметим, что точка q* предъявляет более жесткие требования к настройке налоговой системы по сравнению с точкой q** (q**=2q*).
В точке предельно допустимого налогового бремени (6) максимальная величина фискальных сборов равна: 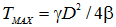 . Данная точка представляет собой чрезвычайно важный индикатор, так как на практике политика фискального регулирования должна строиться по следующему простому принципу: фактическая налоговая нагрузка должна быть не больше величины (6): q<q*. В противном случае бюджет будет проигрывать из-за проводимой государством политики чрезмерной жадности; динамика же производства будет иметь еще менее привлекательный рисунок.
. Данная точка представляет собой чрезвычайно важный индикатор, так как на практике политика фискального регулирования должна строиться по следующему простому принципу: фактическая налоговая нагрузка должна быть не больше величины (6): q<q*. В противном случае бюджет будет проигрывать из-за проводимой государством политики чрезмерной жадности; динамика же производства будет иметь еще менее привлекательный рисунок.
Проблема фискального регулирования инновационного рынка имеет и еще один аспект. Так, если основополагающее условие q<q* выполнено, то это еще не означает, что налоговая нагрузка определена оптимально. В этом случае возникает более тонкая задача по подбору такого уровня налогов, который давал бы максимальный выигрыш в собираемости налогов при умеренном уровне сдерживания производства. Чтобы осуществить соответствующий выбор следует воспользоваться дополнительными индикаторами. Так, для оценки кумулятивного эффекта воздействия той или иной ставки налогов на всю траекторию производства следует воспользоваться интервальным показателем объема произведенной продукции X(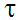 ,q):
,q):
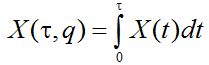 (7)
(7)
где .png) – временной интервал, на котором производится оценка влияния налогов.
– временной интервал, на котором производится оценка влияния налогов.
Аналогичным образом определяется кумулятивная величина фискальных сборов: 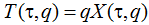 . Тогда для сопоставления двух разных траекторий, различающихся величиной налоговой нагрузки q1 и q2, следует воспользоваться величинами относительного выигрыша в налоговых поступления ΔT(
. Тогда для сопоставления двух разных траекторий, различающихся величиной налоговой нагрузки q1 и q2, следует воспользоваться величинами относительного выигрыша в налоговых поступления ΔT(.png) ,q1,q2) и проигрыша в объеме производства ΔX(
,q1,q2) и проигрыша в объеме производства ΔX(.png) ,q1,q2):
,q1,q2):
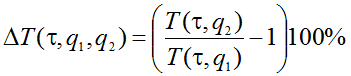 (8)
(8)
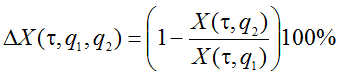 (9)
(9)
Для более полного учета величин налогового выигрыша и производственного проигрыша следует воспользоваться показателем эластичности Е, который позволяется соизмерить, какой процент налогового выигрыша приходится на каждый процент производственного проигрыша:
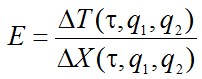 (10)
(10)
На наш взгляд, критерием отбора приемлемых вариантов фискальной политики может служить следующий принцип: E>1. В соответствии с данным подходом относительный выигрыш в налоговых поступлениях должен быть больше, чем относительный проигрыш в объемах производства. В противном случае пополнение государственной казны будет иметь слишком высокую цену в виде подавления активности инновационного предприятия, что, разумеется, никак не может считаться оправданной политикой. Показатели (8)–(10) предполагают проведение многочисленных вычислительных экспериментов для выявления наиболее приемлемых стратегий фискального регулирования. Принцип отбора прост: показатель (9) должен быть минимален, а показатель (10) – максимален (разумеется, при автоматическом выполнении условия E>1).
Для проведения прикладных расчетов можно воспользоваться точными аналитическими формулами для кумулятивных показателей (8) и (9):
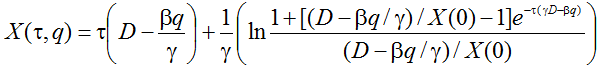 (11)
(11)
(соответственно 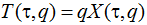 ).
).
Данные выражения недвусмысленно показывают, что исследовать проблему фильтрации «плохих» вариантов фискального регулирования аналитическими методами в общем случае нельзя. Поэтому проблема выбора и переносится в плоскость вычислительных экспериментов. Однако полученное аналитическое выражение (11), а также критическая точка (6) и принцип высокой эластичности E>1 позволяют существенно сократить число возможных экспериментов и целенаправленно продвигаться в направлении выявления лучших вариантов фискального регулирования.
Теперь рассмотрим ряд вопросов, связанных с использованием предложенного подхода на практике. Здесь, на наш взгляд, возможны два принципиально разных варианта – эконометрический и маркетинговый. Рассмотрим их более подробно.
При использовании эконометрического подхода следует построить регрессию следующего вида: .png) , где ΔX(t) – прирост объема производства за время [t;t+1]; α, γ и β – параметры модели, α>0, γ>0 и β>0. На основе оцененных параметров модели легко перейти к параметрам теоретической модели. Для этого необходимо определить потенциальную емкость инновационного рынка по формуле:
, где ΔX(t) – прирост объема производства за время [t;t+1]; α, γ и β – параметры модели, α>0, γ>0 и β>0. На основе оцененных параметров модели легко перейти к параметрам теоретической модели. Для этого необходимо определить потенциальную емкость инновационного рынка по формуле: 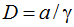 . В дальнейшем система параметров должна быть дополнена показателем фискальной нагрузки q, в качестве которого берется его средняя величина за исследуемый период. После этого все остальные расчеты проводятся автоматически по выведенным нами формулам.
. В дальнейшем система параметров должна быть дополнена показателем фискальной нагрузки q, в качестве которого берется его средняя величина за исследуемый период. После этого все остальные расчеты проводятся автоматически по выведенным нами формулам.
Особенность данного метода состоит в том, что он требует хорошего информационного обеспечения. Так, для построения удовлетворительной со статистической точки зрения регрессии необходимы ретроспективные ряды показателей X(t) и T(t) достаточной длины. Учитывая, что почти все инновационные процессы протекают в соответствии с логистической зависимостью, можно предположить, что конструирование регрессионной модели должно увенчаться успехом.
Идеология использования эконометрического метода такова: имеется информация о развитии инновационного предприятия, которая позволяет на основе регрессии определить роль фискального фактора, а также потенциальную емкость инновационного рынка D, экспансию которого осуществляет изучаемое предприятие. Таким образом, логика исследования идет от микроуровня к макроуровню.
При маркетинговом подходе логика исследования переворачивается и обобщения идут от макроуровня к микроуровню. Данный подход эффективен в тех случаях, когда изучается совсем «молодое» предприятие, в отношении которого еще не существует динамических рядов нужной длины. Такая ситуация вполне типична для новых, только что образованных инновационных предприятий. Алгоритм оценки параметров в данном случае таков. Сначала оценивается потенциальный спрос D на данном инновационном рынке. Затем оцениваются параметры модели, которые находятся в результате решения следующей системы уравнений относительно двух последовательных интервалов времени. Добавив к оцененным параметрам усредненную характеристику налоговой нагрузки q, мы получим полный набор показателей, необходимых для оценки роли налогового фактора для данного инновационного предприятия.
Основной предпосылкой применения маркетингового метода является факт развития предприятия в соответствии с логистическим законом. Учитывая, что данный факт установлен для подавляющего большинства новых и формирующихся рынков и хозяйственных структур, данная посылка может считаться не столь уж большой натяжкой. Если же принять данную посылку, то оценка параметров модели сводится к работе на основе данных только двух примыкающих друг к другу отчетных периодов; длинные статистические ряды в данном случае становятся информационно избыточными.
Теперь рассмотрим применение предложенного маркетингового подхода на условном примере. В данном случае нашей задачей является «прощупывание» как самого алгоритма работы диффузионной модели с фискальным фактором, так и тех числовых закономерностей, которые действуют в инновационной сфере.
Пусть у нас имеется предприятие, которое в начальный момент времени имело следующие характеристики: X0=100; T0=30 (все значения переменных даны в условных денежных единицах). В следующий период прирост продукции составил ΔX0=50. Предположим еще, что проведенный маркетинг показал, что потенциальная емкость рынка производимого продукта равна D=1000. Никаких других данных об истории процесса нет. Необходимо определить область эффективных значений налоговой нагрузки на данное инновационное предприятие.
В данном случае у нас есть информация только за один временной шаг. В этом случае все расчеты можно предельно упростить, рассматривая только одно уравнение за имеющийся временной период и полагая параметр β=1. Тогда имеем однопараметрическую задачу, для которой характерно следующее уравнение:
50=100x(1000–100)γ –30
Расчеты дают следующий результат: γ=0,000888. Тогда легко оценить величину предельно допустимого налогового бремени q*≈44,4%. Таким образом, данное инновационное предприятие не предъявляет серьезных требований к фискальной политике государства: налоговая нагрузка на него должна быть не больше 44% объема его реализации. Если провести вычислительные эксперименты с использованием формул (8)–(11), то можно сузить зону рациональных фискальных стратегий.
Несложно убедиться, что если все исходные параметры предприятия будут в 10 раз меньше, то фискальная нагрузка на предприятие должна практически отсутствовать. Эта ситуация имеет вполне осмысленную интерпретацию, а именно: если изначальная рыночная доля предприятия слишком мала, то никакая фискальная политика не дает положительных результатов. Наш пример показывает, что при значительной начальной рыночной доли предприятия ограничений на фискальную политику почти что нет и для таких инновационных фирм следует использовать стандартный фискальный режим. Для очень молодых и слабых предприятий наоборот необходимы налоговые каникулы хотя бы в течение некоторого времени. Иными словами, фискальная политика государства должна быть чрезвычайно гибкой и зависеть от стадии, в которой находится инновационное предприятие.
За рамками нашего анализа остался вопрос о целесообразности особого налогового режима для инновационных предприятий. Действительно, предлагаемые нами модельные расчеты направлены на уяснение складывающейся ситуации на нарождающемся инновационном рынке и установление такой налоговой нагрузки на инновационное предприятие, которое позволило бы этому предприятию осуществить намечаемую экспансию рынка, а государству – снять с этого процесса максимум налогов. Иногда государству целесообразно существенно снизить налоговую нагрузку на инновационное предприятие относительно среднего уровня. Однако данные действия должны детерминироваться тем обстоятельством, что в противном случае государство вообще может разрушить еще не до конца оформившийся инновационный рынок и не получить с этого вообще ничего. Поэтому в целом предлагаемый механизм представляется вполне оправданным. Разумеется, сама процедура назначения налоговых скидок должна базироваться на четкой экспертизе инновационных предприятий или целых комплексов таких предприятий (отдельных отраслевых сегментов промышленности).
[1] См.: Балацкий Е.В. Анализ влияния налоговой нагрузки на экономический рост с помощью производственно–институциональных функций// «Проблемы прогнозирования», №2, 2003. С.90.
Официальная ссылка на статью:
Балацкий Е.В., Лапин В.И. Диффузионная модель динамики инновационного рынка с учетом налогового фактора// «Финансовый бизнес», №4, 2004. С.36–40.