1. Введение: эконометрика vs нейронные сети
В настоящее время синхронно развиваются два процесса в прикладной экономической науке. Первый предполагает дальнейшее развитие традиционного экономического инструментария – эконометрики, второй ориентирован на поиски и внедрение в аналитическую практику нетрадиционных для экономики методов и средств. В число последних попадает аппарат нейронных сетей, который по своей природе и философии относится к арсеналу инструментария «Big Data».
Попытки построения разнообразных экономических прогнозов с помощью нейросетевых методов часто выступают в качестве альтернативы эконометрических и имитационных моделей. В ряде случаев используются оба инструментария с последующим сравнением результатов и выбором в пользу одного из них [1]. При этом настораживает тот факт, что при решении узких задач, связанных с прогнозированием, выбор в большинстве случаев оказывается за нейронными сетями, что ставит серьезные вопросы перед самой экономической наукой. Суть данной проблемы хорошо выразил лауреат нобелевской премии по экономике Ангус Дитон (Angus Deaton) 22 ноября 2016 г. в ходе ответов на вопросы после своей открытой лекции на III международном форуме в Финансовом университете при Правительстве РФ: «Если у вас есть Big Data, Вы можете не иметь экономической теории». Тем самым сообщество экономистов осознает, что использование в аналитической практике чисто технических методов, не имеющих экономической интерпретации, подрывает их позиции и выхолащивает экономическую науку.
Нейросети не предполагают никакой объяснительной модели, а лишь констатируют тот факт, что некоторый набор переменных может быть преобразован в искомую переменную с достаточно высокой точностью. При этом число входящих переменных может достигать нескольких сотен и даже тысяч, а настройка или обучение сети требует нескольких тысяч эпох (модельных экспериментов). При этом вся та масса переменных, которая не участвует в формировании выходной переменной, не отбраковывается как в эконометрическом моделировании, а нивелируется путем присвоения им минимального или нулевого весового коэффициента. Тем самым нейросетевая модель почти всегда характеризуется большой информационной избыточностью с одновременным отсутствием системного описания сущности моделируемого процесса. Это, пожалуй, главный недостаток нейросетевых моделей и именно он оставляет открытым вопрос о целесообразности широкого применения данного типа моделей в практике экономического прогнозирования. Вместе с тем совершенно недопустимо отрицать плодотворность аппарата нейронных сетей по причине отсутствия в нем рациональных объяснительных схем.
В связи с этим можно поставить вопрос о комбинации двух ведущих вычислительных инструментов – эконометрики и нейронных сетей. В данной статье будет показано, что такая комбинация возможна и дает хорошие результаты. Новизна используемого подхода состоит в использовании двухшаговой процедуры моделирования и краткосрочного прогнозирования инфляции, в которой на первом шаге строится малоразмерная эконометрическая модель, а на втором шаге отобранные регрессоры загружаются в нейронную сеть для последующей калибровки расчетов и повышения точности прогнозов. Такая процедура позволяет сохранить и эффективно совместить объяснительные возможности эконометрических моделей с вычислительными возможностями нейросетей. Предлагаемый подход можно считать универсальным, что позволяет его тиражировать на самый широкий класс задач макроэкономического прогнозирования.
2. Нейронные сети в экономической аналитике: краткий обзор
Как и ранее, сегодня по-прежнему основным инструментарием макроэкономического прогнозирования остается регрессионный анализ с широким набором вспомогательных математических приемов. Однако в силу сложности определения состава и характера влияния объясняющих переменных этот подход далеко не всегда позволяет осуществлять прогнозирование с высокой точностью. Нелинейность взаимосвязей между зависимыми и независимыми переменными зачастую не позволяет определить оптимальную спецификацию эконометрической модели. В последние годы выход из этой ситуации начали искать в построении искусственных нейронных сетей, которые хоть и не имеют четкой аналитической формы, но характеризуются более точными предикативными возможностями.
Первые попытки использования нейросетей в экономическом анализе датируются началом 1990-х гг. В пионерных работах этого времени определялся уровень риска банкротства фирм, исходя из их текущего финансового благополучия [2, 3]. Параллельно с этим направлением нейронные сети нашли применение в оценке уровня возвратности кредитов, выдаваемых частным лицам и организациям [4, 5]. Эти направления со временем перешли из чисто исследовательской сферы в область практического применения: например, Сбербанк России запустил нейронную сеть для оценки залоговой стоимости недвижимости [6].
Помимо группировки субъектов экономической деятельности на уровне микроэкономики, нейросети доказали свою эффективность при прогнозировании макроэкономических показателей. В частности, широкую известность получила модель предсказания ВВП в Канаде [7], в рамках которой были получены более точные прогнозы в долгосрочном периоде по сравнению с традиционными линейными эконометрическими моделями. Аналогичным образом для США было спрогнозировано квартальное изменение ВВП и помесячное изменение индекса промышленного производства [8]. Также был составлен достаточно точный прогноз динамики объема розничных продаж в Соединенных штатах [9].
Постепенно нейросети оказались востребованы в самых разных областях экономического прогнозирования: обменные курсы валют [10]; валовые объемы прибылей корпораций и потребительских расходов [11]; динамика фондовых индексов [12, 13] и т.п. Однако магистральным направлением нейросетевых приложений, которое ежегодно обогащается все новыми работами, признается прогнозирование динамики уровня цен.
Одной из первых работ в этой области стало прогнозирование месячных цен на живой скот и пшеницу в США в 1995 г. [14] Индекс потребительских цен предсказывался для США 1999 г. [15]; результат оказался ожидаемым – нейросеть давала прогнозы точнее регрессионных моделей. Превосходство нейронный сетей над моделями типа интегрированной модели авторегрессии на основе скользящего среднего (ARIMA) и векторной авторегрессии (VAR) было продемонстрировано на примере прогнозирования инфляции в Еврозоне [16]. Исследования в данной сфере охватили как инфляцию в глобальной экономике (например, прогноз инфляции в странах ОЭСР [17]), так и флуктуации уровня цен в отдельных странах (Индия [18], Пакистан [19], Турция [20] и т.д.).
Отечественная научная мысль также не осталась в стороне от генерального инструментального тренда. В 2005 г. было опубликовано исследование, посвященное построению нейросети месячной инфляции в России за 2003–2004 гг. [21]. В качестве зависимых переменных рассматривались: индекс потребительских цен (ИПЦ) на продовольственные товары; ИПЦ на непродовольственные товары; ИПЦ на потребительские услуги; в качестве объясняющей переменной выступал индекс цен производителей с лагами от 0 до 12 месяцев. Более широкий период (с 1991 по 2008 гг.) динамики инфляции в России был интегрирован в нейронную сеть с предпосылкой о зависимости текущего значения уровня цен от аналогичного показателя в каждом из предшествующих 12 месяцев [22]. Удовлетворительные ошибки получились при построении сетей для отдельных периодов, которые авторы работы классифицировали как «интервалы действия определенных экономических тенденций». Достаточно точные прогнозы помесячного изменения ИПЦ были достигнуты при учете более широкого перечня факторов: индексов цен производителей различных групп товаров; индекса тарифов на грузовые перевозки; сводного индекса цен строительной продукции; ВВП и денежной массы (для периода анализа с 2000 по 2010 гг.) [23]. Уровень безработицы и валютный курс также оказались качественными предикторами инфляции в России [1]; модель, основанная на учете только прошлых значений уровня инфляции, дала менее адекватные результаты. Кроме того, в рамках этой работы поквартальное прогнозирование изменения уровня цен дало более точные результаты по сравнению с месячными колебаниями.
Сегодня модели прогнозирования инфляции на основе искусственных нейронных сетей в подавляющем большинстве исследований оцениваются как с точки зрения точности самих прогнозов, так и в сравнении с регрессионными моделями. К сожалению, высокой точности предсказания месячной инфляции на базе нейросетей добиться почти не удается, однако их превосходство над регрессионными моделями, которые также не преуспели в этом деле, демонстрируется в краткосрочном и особенно в долгосрочном периоде.
3. Базовая эконометрическая модель инфляции
Не вдаваясь в детали поиска и отбора факторов инфляции, остановимся только на конечном результате моделирования на основе ежемесячных данных за 2016–2017 гг. Проведенные вычислительные эксперименты позволили получить следующую прикладную эконометрическую модель инфляции:
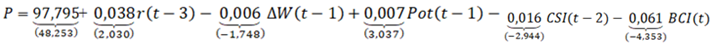 (1)
(1)
N=24; R2=0,805; DW=1,397; E=0,116%,
где P – месячный индекс ИПЦ, %; r – месячный индекс ключевой ставки, %; ∆W – месячный финансово–технологический индекс (производительность труда/заработная плата)*100%; Pot – месячный индекс цен на картофель, %; CSI – индекс потребительских настроений; BCI – индекс предпринимательской уверенности (среди предпринимателей добывающей промышленности); t – индекс текущего месяца. В скобках под коэффициентами регрессии приведены их t–статистики; E – ошибка аппроксимации (в процентах); остальные обозначения – стандартные. Статистические характеристики модели (1) позволяют ее рассматривать в качестве пригодной для прикладных целей.
Построенная модель (1) нуждается в детальном обсуждении.
Дело в том, если ИПЦ учитывать в качестве ежемесячного индекса цен в процентах, то его величина колеблется вокруг 100–процентной отметки, величина которой сама по себе довольно значительна. В этом случае точность модели (1) является фантастической, т.к. ее ошибка составляет десятые доли процента. Такой оптимистичный результат позволяет думать, что построенная модель является в высшей степени удачной и может с высокой эффективностью использоваться для краткосрочного прогнозирования. Однако учет инфляции в виде ее ежемесячных темпов, т.е. ИПЦ минус 100%, дает уже гораздо более умеренные оценки ошибки аппроксимации, хотя и в этом случае точность остается достаточно высокой. Так, из табл.1 видно, что ошибка по годам, равно как и общая ошибка за два года, находятся в пределах 5–6%, что можно считать очень хорошим результатом. Нельзя не отметить и тот факт, что даже в рамках 2–годового периода просматривается определенная неравномерность моделируемого режима: если в первый год происходит переоценка инфляции, то во второй – ее недооценка. Это связано с замедлением борьбы Банка России с инфляцией в 2017 году. В целом же точность модели такова, что рисунок фактической и прогнозной траекторий ИПЦ практически одинаковый, а их тренды почти полностью совпадают (рис.1).
Таблица 1. Распределение накопленной за год ошибки аппроксимации ИПЦ по модели (1), %.
|
Годы |
ИПЦ по модели (1) |
||
|
Расчет |
Факт |
Ошибка |
|
|
2016 |
6,1 |
5,8 |
5,5 |
|
2017 |
2,4 |
2,5 |
–4,5 |
|
Всего |
8,2 |
7,7 |
4,9 |
Источник: расчеты авторов.
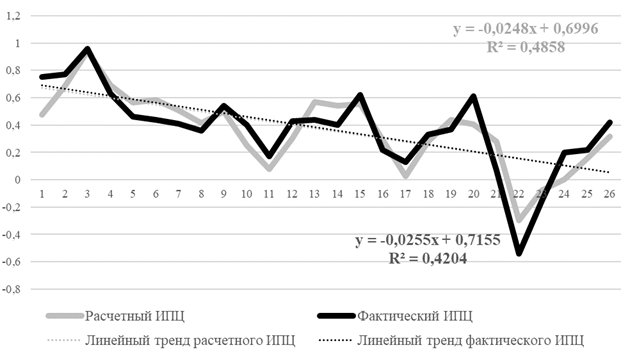
Рис.1. Фактические и расчетные траектории ИПЦ по модели (1).
Источник: расчеты авторов.
Вычислительный эксперимент с прогнозированием инфляции по модели (1) на три месяца вперед на контрольных ретроспективных данных за 11.2017–01.2018 показал, что месячная ошибка относительно темпа инфляции составила 28,77, 24,41 и 97,91% соответственно, что уже выходит за все допустимые рамки погрешности. Данный факт является ключевым для данной работы и предопределяет дальнейшие поиски способов прогнозирования ИПЦ.
4. Фундаментальная проблема атрибуции данных в макроэкономических моделях
Из рис.1 можно видеть почти идеальное наложение трендов фактической и прогнозной траекторий; расчеты показывают, что среднемесячная ошибка между значениями фактического и прогнозного трендов составляет 1,54%. Таким образом, генеральное направление изменения инфляции определяется с поразительной точностью. Ошибки же возникают в результате отклонений фактических и прогнозных значений от своих трендов. Наличие сильных флуктуаций фактических значений ИПЦ вокруг тренда приводит к отсутствию фиксированного диапазона изменений темпов инфляции, в зоне которого происходит реальная динамика. На практике фактические темпы периодически «пробивают» границы предполагаемой зоны устойчивости их значений. Кроме того, наблюдается достаточно четко проявляющаяся цикличность колебаний ИПЦ вокруг линии тренда, что ведет к периодическому усилению волатильности темпов инфляции. И, наконец, даже визуально видно увеличение амплитуды колебаний фактических темпов инфляции по мере снижения их абсолютных значений.
Указанные особенности динамики инфляции осложняют высокоточное краткосрочное (помесячное) прогнозирование инфляции. Эконометрические модели просто принципиально неспособны улавливать столь быстрые оперативные изменения в характере динамики цен. Однако главная проблема в прогнозировании ежемесячных темпов инфляции состоит в их малой величине. Так, в 2017 г. годовой темп инфляции в России составил 2,5%, что эквивалентно среднемесячному темпу в 0,206%. По отношению к этой микроскопической цифре любые ошибки оказываются не просто заметными, а недопустимо большими. Причем подавление инфляции почти до нулевого уровня автоматически приводит к «взрыву» относительной величины ошибки, так как ее величина начинает соотноситься почти с нулем и стремиться к бесконечности.
Надо сказать, что указанная проблема низкой точности является принципиально неразрешимой в рамках факторных эконометрических моделей. Фактически речь идет о глубинном противоречии между макроэкономическим характером конструируемых моделей и микроэкономической величиной моделируемой величины. Так, макромодели (даже прикладные) по самой своей сути направлены на уяснение «грубых», качественных эффектов, тогда как в практике краткосрочного прогнозирования инфляции требуется точность расчетов до второго знака после запятой. Малоразмерные линейные эконометрические модели просто не приспособлены к такой точности. Более того, в них есть и внутреннее противоречие, связанное со стремлением к максимальному уменьшению некоторых макроэкономических параметров почти до нуля, что автоматически ставит непомерные требования к точности прогнозов.
Сегодня существует множество способов и технических приемов обойти указанную проблему, однако ни один из них не может считаться универсальным и по-настоящему действенным. В связи с этим ниже будет предложена простая эвристическая процедура прогнозирования ИПЦ на базе модели (2).
Указанное противоречие между макроэкономической природой конструируемых прогнозных моделей с микроэкономической величиной выходной переменной будем называть фундаментальной проблемой атрибуции данных в макромоделях (ПАДМ).
Данное название, на наш взгляд, является обоснованным и полностью соответствует классическому пониманию рассматриваемого явления. В данном случае речь идет о том, что у аналитиков просматривается склонность объяснять ситуативные флуктуации ИПЦ диспозиционными (макроэкономическими) факторами. В практике прогнозирования данный эффект порождает невозможность «поймать» флуктуации агрегированного индекса цен с помощью малоразмерных эконометрических моделей.
Надо сказать, что данная проблемы так или иначе уже и раньше возникала в экономической науке. Достаточно указать на наличие огромного арсенала моделей формирования валютных курсов, которые основаны на совершенно разных теориях и группах объясняющих факторов. Такой плюрализм инструментальных подходов объясняется тем, что все модели «разводятся» по критерию временного кванта моделирования: одни направлены на прогнозирования каждодневных эффектов, другие – недельных, третьи – месячных, четвертые – квартальных и т.д. [24]. Иными словами, на разных временных отрезках действуют разные механизмы курсообразования. Разумеется, степень грубости используемых статистических агрегатов в таких моделях прямо пропорциональна величине временного кванта: чем больше период прогнозирования, тем более грубыми являются факторы, определяющие выходную величину, и тем меньше предъявляется требований к точности прогнозов.
В нашем случае ПАДМ продуцируется не совсем адекватным модельным аппаратом, используемым для прогнозирования инфляции со слишком малым временным квантом. Наличие неудовлетворительной точности прогнозов инфляции на основе эконометрических моделей продуцирует поиски технических подходов, которые позволили бы нивелировать ПАДМ.
5. Двухшаговая процедура прогнозирования инфляции: идеология и общие контуры
В настоящее время имеется большое число различных модельных инструментариев, с помощью которых ведется прогнозирование инфляции. Более того, для повышения качества прогнозных оценок строятся синтетические прогнозы, представляющие собой некое усреднение прогнозов, полученных разными методами. Нами же ниже предлагается несколько иной подход комплексного использования двух разных типов моделирования, а именно: эконометрическое моделирование и нейронная сеть «запускаются» в последовательно режиме. Раскроем суть предлагаемого подхода подробнее.
В данном случае вся процедура прогнозирования инфляции представляет два шага. На первом шаге строится малоразмерная эконометрическая модель инфляции (1) (далее будем ее обозначать как Eco–1, чтобы подчеркнуть ее эконометрическую природу), которая обеспечивает: отбор факторов влияния (регрессоров); объяснение процесса колебания значений ИПЦ; достаточно корректное воспроизведение фактического рисунка динамики инфляции. Однако, как уже указывалось ранее, главным камнем преткновения на этом этапе является слишком большая ошибка относительно прогнозных значений. Для устранения этого недостатка осуществляется второй шаг, предполагающий загрузку в нейронную сеть полученных в модели Eco-1 факторов инфляции с дальнейшей калибровкой расчетов с целью повышению точности прогнозных оценок.
Указанная процедура обладает целым рядом преимущество по сравнению с автономным использованием каждого типа инструментария – эконометрической модели и нейронной сети.
Во-первых, наличие модели Eco–1 позволяет сохранить теоретическую основу моделируемого процесса, очистить моделируемый процесс от незначимых факторов («шумов») и ограничиться небольшим числом понятных и хорошо верифицируемых факторов. Последующая чисто механистическая обработка базовой зависимости с помощью нейросети осуществляется уже для теоретически осмысленной зависимости, а не для хаотичного набора огромного числа потенциальных регрессоров.
Во-вторых, использование арсенала нейронной сети позволяет существенно повысить точность прогнозов за счет ее обучения без потери объяснительной способности общей модельной схемы. Фактически настройка нейросети и калибровка выходной переменной позволяют «превратить» теоретическую эконометрическую конструкцию Eco–1 в практически значимую модель, способную выдавать адекватные прогнозы.
В-третьих, наличие небольшого числа регрессоров в модели Eco–1 позволяет максимально экономно использовать вычислительные возможности нейросети и повысить эффективность работы с ней. Данный результат достигается за счет загрузки в нейросеть не сотен и тысяч потенциальных факторов инфляции, а только пяти регрессоров, уже прошедших статистические тесты и заведомо являющихся значимыми факторами процесса роста цен. Такое резкое усечение входных данных ведет к сокращению промежуточных слоев и в модели и числа эпох (экспериментов). Фактически это означает, что эффективная настройка нейросети требует вместо нескольких тысяч всего лишь несколько десятков эпох. Тем самым нейросеть не перегружается ненужными данными и дает возможность получить нужный результат в самые сжатые сроки.
Предложенная синтетическая процедура моделирования отличается от общепринятых. Например, традиционная схема синтеза предполагает параллельное прогнозирование инфляции на основе разных инструментариев (например, на основе эконометрических моделей и нейросетей) с получением вектора прогнозных оценок, который потом «сжимается» в одну оценку с помощью той или иной вычислительной операции. Наш подход предполагает последовательное использование разных инструментариев (эконометрических моделей и нейросетей) с получением итоговой скалярной прогнозной оценки. Тем самым нами создается своеобразный модельный комплекс, когда выходные характеристики одного инструментария (эконометрической модели) используются в качестве входных данных другого (нейронной сети) с получением консолидированного прогноза.
Важный плюс последовательной интеграции разных способов моделирования при прогнозировании инфляции состоит не в противопоставлении этих способов, а в их взаимном дополнении. Именно такое эффективное сопряжение двух видов инструментариев позволяет достигать качественно новых результатов на основе возникающего эффекта синергии.
6. Нейросетевая модель инфляции и особенности ее обучения
При построении искусственных нейронных сетей для предсказания экономических переменных на основе временных рядов не существует четких алгоритмов создания и улучшения модели. Из ранее приведенного анализа литературы можно вычленить следующие особенности построения нейросетей при прогнозировании макроэкономических величин:
– используются 1 или 2 скрытых слоев;
– количество нейронов не превышает число переменных входного слоя;
– обучение модели требует прохождения в среднем 3000 эпох;
– в качестве активационной функции обычно применяется гиперболический тангенс.
Процесс создания нейронной сети сводится к учету двух важных правил. С одной стороны, малое количество скрытых слоев или прохождение небольшого числа эпох приводит к тому, что нейросеть может быть недообучена, т.е. будет она будет генерировать высокую ошибку на тестовой выборке с крайне низким шансом получения точных прогнозов. С другой стороны, избыточные скрытые слои, чрезмерное число нейронов в них и отсутствие ограничений на число эпох является предпосылкой к переобучению сети, т.е. на выходе будет максимально точное описание влияния переменных на тестовых данных на фоне неверных прогнозов.
В нашем случае опасность недообучения нейросети практически исключена в силу малого числа входных переменных (5 показателей). Чтобы избежать опасности переобучения нами будет использован дополнительный фильтр на точность (подробнее об этом ниже).
При выборе в нейросети активационной функции важно учитывать характер связей, которые могут возникать между переменными. Например, в экономическом моделировании повсеместно распространены системы с положительными и отрицательными эффектами. В таких случаях, как правило, используется функция гиперболического тангенса, которая центрирована относительно нуля и выступает более подходящим инструментом по сравнению, например, с сигмоидой, принимающей значения от 0 до 1.
Создание нейронной сети Web–1 выполнено в программном продукте RStudio (пакет «neuralnet»). Процесс построения сети состоял из двух последовательных этапов ее обучения. На первом этапе обучение сети велось на основных ретроспективных данных (февраль 2016 г. – октябрь 2017 г.) с использованием критерия минимизации суммы квадратов ошибок. На втором этапе обучение велось на тестовых прогнозных данных, в качестве которых использовались последние три месяца ретроспективного ряда (ноябрь 2017 г. – январь 2018 г.); в качестве критерия точности использовалась минимизация средней абсолютной ошибки прогнозов.
Следует отметить, что примененный нами подход не является широко распространенным, поскольку обычно точность прогнозов считается главным признаком качества нейронной сети. В данном случае мы как бы усилили традиционный подход, введя два фильтра точности – основной (по ретроспективным данным) и дополнительный (по тестовым прогнозам).
Предварительно все данные модели Web-1 были нормализированы по стандартной формуле Xnorm=(Х–Xmin)/(Xmax–Xmin). Минимальная средняя ошибка прогнозов нормированных значений (0,5%) была достигнута при ошибке на тестовой выборке (0,7%) при следующих условиях: два скрытых слоя по 5 и 1 нейрону; 1121 эпоха обучения сети; активационная функция – гиперболический тангенс; функция ошибок задана через сумму квадратов ошибок; исключена активационная функция при переходе к выходному слою нейронов. Остальные параметры оказывали незначительное воздействие на процесс обучения. Структура наиболее эффективной нейронной сети представлена на рис.2.
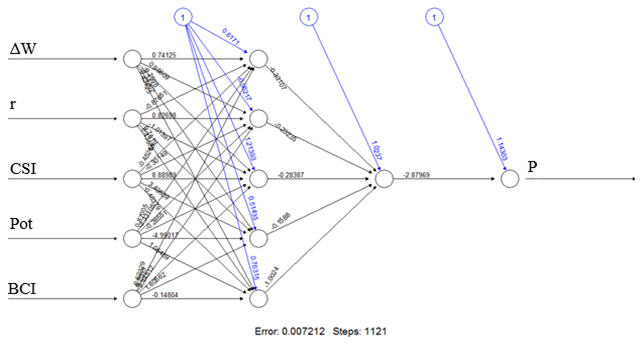
Рис.2. Структура нейронной сети ИПЦ.
Источник: расчеты авторов.
Для понимания степени успешности построенной модели Web–1 необходимо сравнить качество тестовых прогнозов темпов инфляции, полученных на основе эконометрической модели Eco–1 и модели Web–1. Как видно из табл.2, преимущество нейросети по критерию точности прогноза является тотальным. При этом главным обстоятельством здесь выступает тот факт, что по данному критерию использовать в аналитической практике модель Eco–1 категорически нельзя, тогда модель Web–1 – можно. Тем самым второй шаг в построении модели инфляции путем калибровки эконометрической зависимости Eco–1 посредством нейросети себя полностью оправдал.
Таблица 2. Прогнозы темпов инфляции по моделям Eco–1 и Web–1
|
Прогнозный период |
Фактический темп инфляции |
Прогноз темпов инфляции |
|
|
по модели Eco–1 |
по модели Web–1 |
||
|
Ноябрь 2017 |
0,22 |
0,1567 |
0,2269 |
|
Декабрь 2017 |
0,42 |
0,3174 |
0,4265 |
|
Январь 2018 |
0,31 |
0,0065 |
0,3141 |
|
Средняя ошибка аппроксимации прогноза, % |
– |
50,4 |
2,0 |
Источник: расчеты авторов.
Нельзя не отметить, что сравнение между собой модели Eco–1, выбранной по параметрам качества объяснения зависимости (коэффициент детерминации, значимость коэффициентов при переменных и т.д.), и нейросети Web–1, отобранной исключительно по признаку точности прогноза, содержит в себе определенный элемент несправедливости – преимущество нейросети изначально предопределено. Однако само это сравнение призвано показать не прогностический потенциал нейросети самой по себе, а ее возможности по повышению предикативных свойств первичной эконометрической модели Eco–1. При этом хорошие статистические параметры регрессионной модели Eco–1, как правило, гарантируют весьма точные прогнозы по модели Web–1, в то время как применительно к нейросетевым моделям, построенным в автономном режиме (без предварительного отбора факторов с помощью модели Eco–1), такой гарантии нет из-за отмеченного ранее риска переобучения.
В целом подчеркнем, что двухшаговая процедура прогнозирования представляет собой последовательное сочленение эконометрической и нейросетевой моделей, в связи с саму искомую синтетическую модель будем обозначать Eco–1/Web–1.
7. Заключение
Апробированный в данной статье подход к прогнозированию инфляции, предполагающий двухшаговую процедуру моделирования с помощью эконометрического аппарата и нейронных сетей позволил получить результата, который обладает рядом преимуществ по сравнению с уже предлагавшимися подходами.
Во-первых, последовательное использование двух типов моделирования в аналитической конструкции Eco–1/Web–1 снимает противоречие между ними. Как оказывается, они могут не только конкурировать между собой, но и эффективно дополнять друг друга. Не исключено, что похожие последовательные сопряжения разнотипных моделей могут быть реализованы и для других классов прогнозных инструментариев. На наш взгляд, такой подход представляется весьма перспективным и может быть тиражирован на другие модельные схемы.
Во-вторых, построенная синтетическая модель прогноза инфляции Eco–1/Web–1 позволила объединить в себе два ключевых достоинства имеющихся методов – адекватную теоретическую схему моделируемого процесса роста цен и высокую точность аппроксимации выходной переменной, в том числе и для прогнозных значений.
В-третьих, калибровка модели Eco–1/Web–1 до поразительно высокой точности прогнозных оценок позволила продемонстрировать не только принципиальную возможность решения фундаментальной ПАДМ, но и наметить путь, который ведет к этому решению. Можно сделать предварительный вывод, согласно которому повышение точности макромоделей для малых значений переменных предполагает специальный калибрующий фильтр наподобие нейронной сети. Более того, не исключено, что все виды модельного инструментария, не относящиеся изначально к экономическому, могут быть применены для решения экономических задач только «на подхвате», т.е., как в нашем случае, для калибровки результатов на завершающей стадии исследования.
Практическая работа с моделью Eco–1/Web–1 предполагает ее периодическое обновление либо на основе скользящей выборки, когда старые данные отсекаются и заменяются новыми, либо на основе дополненной, когда к старому временному ряду добавляются новые данные. При этом пересчету подвергаются обе части модельного комплекса – как Eco–1, так и Web–1. Вместе с тем хотелось бы подчеркнуть, что указанное обновление не предполагает ежемесячного режима; скорее всего, корректировка модели должна производиться раз в 3–4 месяца. Такая периодичность обновления позволит «сохранять» построенную модель в течение разумного времени для практической работы, после чего она все-таки будет нуждаться в перенастройке.
Список использованных источников
1. Горшкова Т., Синельникова Е. Сравнительный анализ прогнозных свойств моделей российской инфляции // Научный вестник ИЭП им. Гайдара. 2016. №. 6. С. 34–41.
2. Odom M.D., Sharda R. A neural network model for bankruptcy prediction // Neural Networks, 1990. IJCNN International Joint Conference. 1990. P. 163–168.
3. Rahimian E. et al. Bankruptcy prediction by neural network // Neural networks in finance and investing. 1993. P. 159–176.
4. Marose R.A. A financial neural-network application // AI Expert. 1990. Vol. 5(5). P. 50–53.
5. Jagielska I., Jaworski J. Neural network for predicting the performance of credit card accounts // Computational Economics. 1996. Vol. 9(1). P. 77–82.
6. ТАСС. Сбербанк запустил первую в России систему оценки недвижимости с помощью нейросети. [Электронный ресурс]. Режим доступа: http://tass.ru/ekonomika/4943437.
7. Tkacz G. Neural network forecasting of Canadian GDP growth // International Journal of Forecasting. 2001. Vol. 17(1). P. 57–69.
8. Aminian F. et al. Forecasting economic data with neural networks // Computational Economics. 2006. Vol. 28(1). P. 71–88.
9. Alon I., Qi M., Sadowski R.J. Forecasting aggregate retail sales: a comparison of artificial neural net-works and traditional methods // Journal of Retailing and Consumer Services. 2001. Vol .8(3). P. 147–156.
10. Kuan C. M., Liu T. Forecasting exchange rates using feedforward and recurrent neural networks // Journal of applied econometrics. 1995. Vol. 10(4). P. 347–364.
11. Swanson N.R., White H. A model selection approach to real-time macroeconomic forecasting using linear models and artificial neural networks // Review of Economics and Statistics. 1997. Vol. 79(4). P. 540–550.
12. Chen A.S., Leung M.T., Daouk H. Application of neural networks to an emerging financial market: forecasting and trading the Taiwan Stock Index // Computers & Operations Research. 2003. Vol. 30(6). P. 901–923.
13. Shen W. et al. Forecasting stock indices using radial basis function neural networks optimized by arti–ficial fish swarm algorithm // Knowledge–Based Systems. 2011. Vol. 24(3). P. 378–385.
14. Kohzadi N., Boyd M.S. Testing for chaos and nonlinear dynamics in cattle prices //Canadian Journal of Agricultural Economics. 1995. Vol. 43(3). P. 475–484.
15. Aiken M. Using a neural network to forecast inflation // Industrial Management & Data Systems. 1999. Vol. 99(7). P. 296–301.
16. Binner J.M. et al. A comparison of linear forecasting models and neural networks: an application to Euro inflation and Euro Divisia // Applied economics. 2005. Vol. 37(6). P. 665–680.
17. Choudhary M.A., Haider A. Neural network models for inflation forecasting: an appraisal // Applied Economics. 2012. Vol. 44(20). P. 2631–2635.
18. Thakur G.S.M., Bhattacharyya R., Mondal S.S. Artificial neural network based model for forecasting of inflation in India // Fuzzy Information and Engineering. 2016. Vol. 8(1). P. 87–100.
19. Haider A., Hanif M.N. Inflation forecasting in Pakistan using artificial neural networks //Pakistan economic and social review. 2009. P. 123–138.
20. Catik A.N., Karaçuka M. A comparative analysis of alternative univariate time series models in forecasting Turkish inflation //Journal of Business Economics and Management. 2012. Vol. 13(2). P. 275–293.
21. Зарова Е.В., Заров И.К. Нейронные сети как средство моделирования и прогнозирования инфляционных процессов // Вестник Самарского государственного технического университета. Серия Физико-математические науки. 2005. № 34. С. 182–186.
22. Коваленко А.В., Уртенов М.Х. Нейросетевое моделирование инфляции в России // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2010. №. 61. С. 278 – 297.
23. Огородов А.П. Учет влияния ряда факторов при прогнозировании инфляционных процессов на базе нейронных сетей // Электроника и информационные технологии. 2011. № 1. [Электронный ресурс]. Режим доступа:fetmag.mrsu.ru/2011-1/pdf/Forecasting_Of_Inflationary.pdf.
24. Балацкий Е.В. Факторы формирования валютных курсов: плюрализм моделей, теорий и концепций// Мировая экономика и международные отношения. 2003. №1. С.46–58.
Официальная ссылка на статью:
Балацкий Е.В., Юревич М.А. Использование нейронных сетей для прогнозирования инфляции: новые возможности// «Вестник УрФУ. Серия экономика и управление», Том 17, №5, 2018. С.823–838.