Объективность неравномерного экономического развития (краткий обзор теоретических моделей)
Экономическое развитие представляет собой процесс смены состояний относительного избытка и недостатка материальных благ. Иначе говоря, экономическая система функционирует в самоподдерживающемся режиме «перенакопление – дефицит». На сегодняшний день имеется обширная литература по теории экономического цикла, где исследуется возникновение как экзогенных, так и эндогенных экономических колебаний. Наибольший интерес для нас представляют модели, предполагающие рождение эндогенных циклов.
Среди обилия подобного рода работ следует особо выделить экономические модели типа «хищник – жертва», базирующиеся на гипотезе В.Вольтерра о встрече и формальном аппарате теории динамических систем. К числу таких моделей относится модель товарообмена В.П.Милованова, описывающая межрыночные (взаимодействия и, в частности, взаимодействие товарного и денежного рынков (сущность моделируемого процесса – встреча, конкуренция, обмен и выбор товаров на потребительских рынках [1]). Другим характерным примером является модель согласования движения рабочих мест с движением рабочей силы (модель Наумова–Коровкина), которая описывает обменные процессы внутри рынка труда (сущность моделируемого процесса – переход «потенциальных работников» на вакантные рабочие места [2]). Отражая сложный динамический процесс перекрестного взаимодействия и взаимной самонастройки экономических популяций, модели типа «хищник – жертва» в большинстве случаев предполагают неустойчивые, в том числе колебательные, решения. Таким образом, механизм взаимной адаптации экономических рынков и их элементов объективно приводит к неравномерности экономического развития.
Другой класс моделей основан на идее восстанавливания экономического равновесия путем его адаптивного «нащупывания». Так, например, модель Чанга–Смита описывает процесс настройки выпуска на отклонение инвестиций от сбережений при заданной динамике накопления основного капитала. В модели В.Торре отображается процесс адаптации выпуска на отклонение инвестиций от сбережений и ставки процента на избыточное предложение денег. Аналогичная схема «нащупывания» реализуется в моделях X.Роуза и Дж.Бенасси [3]. Для подобных моделей, как правило, характерно наличие предельного цикла при определенных величинах эластичностей исследуемых макрохарактеристик. Таким образом, при достижении необходимой степени чувствительности ключевых макропеременных на экономические возмущения для системы характерна неравномерность функционирования.
Большинство простых динамических моделей, как правило, сводится к системе динамических дифференциальных уравнений. Такова, например, инновационно-экономическая маятниковая модель С.В.Дубовского, интегрирующая в себе динамику выпуска, капитала и технологического уровня [4]. Формальный анализ ее решений показывает наличие периодических колебаний и позволяет выявить целый ряд свойств кондратьевского цикла, в основе которого лежит процесс истощения технологического потенциала по мере роста экономической активности. Таким образом, механизм колебаний в такого рода моделях идентичен механизму в моделях «хищник – жертва».
Помимо моделей, в той или иной форме учитывающих динамическую чувствительность к взаимным изменениям экономических сегментов и характеризующих их макропоказателей, имеется обширный класс моделей, отражающих эффект действия положительных прямых и обратных связей. Это прежде всего классические модели мультипликатора–акселератора П.Самуэльсона, Дж.Хикса и Р.Гудвина. Данные модели представляют собой динамические уравнения, переменные которых обладают свойством «динамической автозависимости» и сводятся к дифференциальным или разностным уравнениям. При достаточно сильной выраженности данного свойства в системе возникают колебательные процессы.
Достаточно интересную группу моделей продуцирует учет эффекта временных запаздываний. Так, например, одними из классических моделей ценообразования являются линейно–интегральная модель Ф.Дреша и ее модификации, которые предусматривают колебательные режимы для динамики цен [5]. Источником флуктуаций здесь является кумулятивное напряжение (дисбаланс) на товарном рынке, порождающее в системе информационные волны и неустойчивость цен. Примером влияния распределенных временных лагов на циклическую динамику инвестиций является модель равновесных колебаний С.П.Аукуционека [6].
Помимо «чистых» аналитических моделей имеются модельные построения смешанного типа. Так, например, в аналитико–имитационной модели В.В.Попова циклические колебания обусловлены механизмом воздействия неравномерного выбытия основного капитала на динамику нормы прибыли (сущность моделируемого процесса – динамическая взаимосвязь нормы прибыли со сроком службы основного капитала и связь основных макропеременных с нормой прибыли [7]).
Образцом синтеза процесса взаимодействия экономических сегментов (в том числе различных слоев населения) с учетом временных запаздываний и субъективных предпочтений во времени являются так называемые модели перекрывающихся (перекрещивающихся) поколений, которые в ряде случаев дают иррегулярные колебательные решения. Это прежде всего модели П.Самуэльсона, Дж.Бенхабиба и Р.Дэя, Ж.–М.Грандмо, П.Даймонда, Б.Джулиена. Сложный колебательный рисунок динамики макропеременных в таких моделях продуцируется, как правило, сильными предпочтениями потребителей во времени и разнонаправленностью межвременных эффектов дохода и замещения. Характерно, что модели статической оптимизации (нелинейного программирования) в данном случае сводятся к дифференциальным или разностным уравнениям, позволяющим в явном виде исследовать динамические свойства экономической системы. Имеются также работы по изучению цикличности экономических процессов с помощью простых статических оптимизационных моделей с последующим «полуформальным» динамическим анализом. К такого рода моделям относится модель синдрома дефицита М.Л.Вейцмана, из которой вытекает циклическая динамика образования потребительских запасов в условиях товарного дефицита. Искомая кривая имеет пилообразную форму, которая обусловлена стремлением потребителя минимизировать усилия по приобретению потребительских благ [8].
Таким образом, закономерность неравномерного экономического развития является, на наш взгляд, вполне доказанной с различных точек зрения благодаря использованию многообразных теоретико–методологических подходов. Тем не менее несмотря на обилие существующих моделей делового цикла в экономической теории пока все же остаются «белые пятна», касающиеся неравномерности экономической динамики. Ниже мы рассмотрим возможность появления «сильных» динамических флуктуаций в сфере производства и потребления с позиций, ранее не фигурировавших в аналитических построениях. Более конкретно задача представленного исследования заключается в строгом доказательстве факта возможного возникновения динамически неустойчивых системных «ячеек» в сферах производства и потребления даже в самых «безобидных» условиях. Именно факт сосуществования устойчивых и неустойчивых элементов экономической системы при стационарной результирующей их взаимодействия и будет предметом рассмотрения данной статьи.
Модель возникновения потребительских флуктуаций
Рассмотрим совокупность потребительских благ (для определенности будем полагать материальные блага) xj, j=1, т, которые приобретаются и потребляются экономическим субъектом. В соответствии с теорией субъективной полезности стратегия потребления этого блага зависит от функции его полезности U=U(X) (X – вектор потребительских благ); вид и форма кривой функции полезности предопределяет динамику потребления X(t), где t – время. Поскольку потребление изменяется во времени, то имеем U=U[X(t)], т. е. функция полезности потребительских благ зависит от времени опосредованно – через динамику их объемов. Данный методологический прием, позволяющий связать величину функции полезности со временем, достаточно важен и интересен, так как несмотря на то что в экономической теории свойства статической функции полезности U=U(X) достаточно хорошо изучены (как правило, такие зависимости выражаются логарифмическими и степенными функциями), закономерности изменения динамической функции полезности U=U(t) до сих пор практически не рассматривались. Таким образом, зависимость U=U[X(t)] позволяет «динамизировать» дальнейшие построения.
Учитывая сегментированность товарного рынка и множественность потребительских благ, агрегатная функция полезности U может быть представлена в виде аддитивной функции полезности
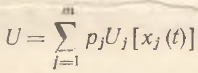
где Uj – частная полезность потребляемого j-го блага; весовые коэффициенты рj задают шкалу относительной значимости рассматриваемых благ (аналогичные построения возможны и при рассмотрении макроэкономики в целом; в этом случае U будет характеризоваться благосостояние общества, a pj=∂U/∂Uj – предельную социальную значимость j–ой группы потребительских благ). Несмотря на то что данный частный вид агрегатной функции полезности весьма упрощенно отражает действительность, его рассмотрение является позитивным подходом к принципиальному пониманию процесса из-за простоты последующих формальных конструкций. Заметим, что в теоретических исследованиях различные модификации аддитивных функций полезности используются достаточно широко. В дальнейшем без потери степени общности для проводимого анализа будем рассматривать лишь два потребительских блага: i и l. Такой прием вполне правомерен, так как любой набор благ может объединяться в небольшое число групповых благ. Таким образом, свертка всего потребительского множества в двухфакторную конструкцию – это лишь проблема соответствующего способа агрегирования (обобщение на m–мерный случай будет представлено ниже).
Исходя из сказанного, можно записать следующие условия первого и второго порядка для функции полезности:
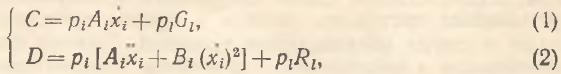
где 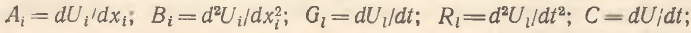 D=d2U/dt2. Понятно, что в общем случае величины Ai, Bi, Gl, Rl, С и D зависят от времени. Таким образом, система (1) – (2) позволяет определить стратегию потребителя xi(t) при заданных временных траекториях Ai(t), Bi(t), Gl(t), Rl(t), C(t) и D(t). При этом Ai(t) и Bi(t) отражают динамику вкусов и предпочтений потребителя во времени, Gl(t) и Rl(t) фиксируют скорость и ускорение, с которыми потребитель предполагает наращивать (уменьшать) полезность от владения благом xl, a C(t) и D(t) характеризуют скоростные свойства роста агрегатной функции полезности.
D=d2U/dt2. Понятно, что в общем случае величины Ai, Bi, Gl, Rl, С и D зависят от времени. Таким образом, система (1) – (2) позволяет определить стратегию потребителя xi(t) при заданных временных траекториях Ai(t), Bi(t), Gl(t), Rl(t), C(t) и D(t). При этом Ai(t) и Bi(t) отражают динамику вкусов и предпочтений потребителя во времени, Gl(t) и Rl(t) фиксируют скорость и ускорение, с которыми потребитель предполагает наращивать (уменьшать) полезность от владения благом xl, a C(t) и D(t) характеризуют скоростные свойства роста агрегатной функции полезности.
Если ввести характеристику темпа ускорения агрегатной полезности во времени α=D/C, то система (1) – (2) редуцируется к следующему уравнению:
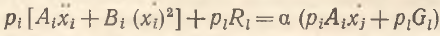 (3)
(3)
Рассмотрим частный, но очень важный случай. Так, если r=C/U – темп прироста полезности и он постоянен во времени, то α=r. В модели (3) показатель r позволяет отобразить направление изменения агрегатной функции полезности с учетом эффекта масштаба потребления. Пусть прирост частной полезности l-го блага также стабилен: Gl=const. Тогда Rl=0 и уравнение (3) в этом случае принимает вид
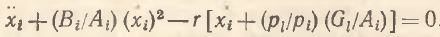 (4)
(4)
Введя показатель абсолютной антипатии к потреблению 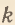 i=–Bi/Ai, обозначив ω=rplGl/piAi и полагая ω=const, а также опуская в дальнейшем индекс i, уравнение (4) окончательно сводится к следующему виду:
i=–Bi/Ai, обозначив ω=rplGl/piAi и полагая ω=const, а также опуская в дальнейшем индекс i, уравнение (4) окончательно сводится к следующему виду:
(r + .png) ẋ) ẋ – ẍ + ω = 0 (5)
ẋ) ẋ – ẍ + ω = 0 (5)
Данная модель является достаточно грубой, будучи лишь первым приближением моделируемого процесса. В дальнейшем уравнение (5) будет уточняться и детализироваться, однако его математическая структура останется неизменной.
В соответствии с ортодоксальной теорией полезности Ai>0 (в силу аксиомы ненасыщения), а Bi<0 (в силу закона Госсена) [9]. Одновременно с этим вкусы и предпочтения потребителей, по мнению А. Маршалла, со временем изменяются благодаря выработке соответствующих потребительских привычек («пристрастий» и «антипристрастий»), что означает изменение Аi, и Вi, pi и pl во времени. При этом если Аi и Вi характеризуют кривую полезности в зависимости от монотонного изменения xi, то величины С и D дают ясную характеристику полезности в зависимости от монотонного изменения времени. В этом смысле уравнение (5) задает траекторию потребления в зависимости от меняющихся вкусов и пристрастий потребителя при реализации им «принудительной» (целевой) стратегии в отношении увеличения своего благосостояния. Однако в соответствии с экономической доктриной Беккера–Стиглера, которая в настоящее время доминирует в экономической теории, вкусы и предпочтения потребителя полагаются стабильными во времени [10]. Это эквивалентно тому, что показатели .png) и ω в уравнении (5) не зависят от времени и вместе с r выступают в качестве параметров модели.
и ω в уравнении (5) не зависят от времени и вместе с r выступают в качестве параметров модели.
Здесь и в дальнейшем при изучении закономерностей динамики потребления мы будем абстрагироваться от тех социально–психологических факторов, которые оказывают на нее какое-либо влияние. Следуя этой линии рассуждения, мы не рассматриваем роль так называемого человеческого капитала, который в теории Стиглера – Беккера имеет ключевое значение. Подобная методологическая «узость» проводимого анализа представляется вполне оправданной, так как нас интересуют исключительно временные аспекты потребления. Тем самым центр тяжести теоретических построений переносится на выяснение «внешних» сил, формирующих динамику потребления, а не «внутренних» факторов, которые сами испытывают сильнейшие воздействия извне. Иными словами, динамика потребления оказывается зависимой от «чистых», рафинированных преференций субъекта в отношении потребительских благ и не зависит от структуры его постоянно эволюционирующей личности. Несмотря на столь явное огрубление действительности, именно такой подход является эффективным, так как позволяет понять законы потребления в абсолютно стабильной социальнопсихологической среде, что является необходимым первым шагом к изучению более сложных экономических эффектов.
Таким образом, уравнение (5) описывает динамику потребления i-го блага в стационарной экономике, под которой в широком смысле слова понимается экономика с постоянными во времени характеристиками роста [11]. Именно такой тип экономики будет рассматриваться в данной работе. Подобный подход позволяет доказать следующее предварительное утверждение о рождении потребительских флуктуаций в условиях стабильности вкусов экономических агентов: стратегия, обеспечивающая потребителю постоянный заданный темп прироста благосостояния (полезности) при стабильности его вкусов и предпочтений, описывается уравнением (5); при выполнении закона Госсена (закона убывания предельной полезности) и аксиомы ненасыщения для Gi=const>0 и 4.png) (pl/pi)(Gl/Ai)>r данная стратегия носит принципиально неустойчивый характер [12].
(pl/pi)(Gl/Ai)>r данная стратегия носит принципиально неустойчивый характер [12].
Содержательно сформулированное утверждение означает следующее: при определенной потребительской консервативности экономический агент, стремящийся наращивать свое благосостояние (полезность) достаточно плавным образом, оказывается, должен приобретать и потреблять блага отнюдь не равномерно. Причем динамика x(t) характеризуется достаточно резкой сменой «провалов» в потреблении со столь же стремительными всплесками потребительского спроса (рисунок). Следовательно, стабильность вкусов экономического агента сама по себе, как оказывается, не гарантирует от возникновения эндогенных флуктуаций в спросе и потреблении. Данный вывод на первый взгляд представляется парадоксальным, так как правомерно было бы ожидать, что в подобных условиях потребительская стратегия должна выражаться гладкой функцией. По-видимому, это один из тех случаев, когда кратчайший путь не является оптимальным.
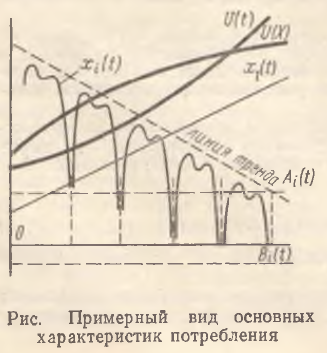
Заметим, что утверждение сформулировано для ситуации с достаточно большим числом степеней свободы. Некоторые экономические факторы отражены в параметрах уравнения (5). Так, например, срок службы товара, а также интенсивность его физического и морального износа косвенным образом аккумулируются в показателе абсолютной антипатии к потреблению. Однако в модели (5) не учитываются бюджетные ограничения, возможность создания запасов, дискретность экономических сделок и процессов потребления и ценообразования, не отображены ценовые эффекты, а также динамические эффекты замены и взаимодополняемости благ (в этом смысле .png) представляет собой свертку «чистых» потребительских вкусов и преференций, а показатель r – свертку скоростных показателей стратегии потребителя в отношении своего благосостояния). В реальности же все перечисленные ограничения фигурируют в качестве активных, что деформирует гипотетические траектории потребления, а также сами потребительские установки. Формально это означает, что учет указанных эффектов будет способствовать аберрации исходной кривой x(t) (рисунок) и «срезать» или, наоборот, усиливать флуктуации в решении (6).
представляет собой свертку «чистых» потребительских вкусов и преференций, а показатель r – свертку скоростных показателей стратегии потребителя в отношении своего благосостояния). В реальности же все перечисленные ограничения фигурируют в качестве активных, что деформирует гипотетические траектории потребления, а также сами потребительские установки. Формально это означает, что учет указанных эффектов будет способствовать аберрации исходной кривой x(t) (рисунок) и «срезать» или, наоборот, усиливать флуктуации в решении (6).
Потребительские дисконты как источник колебаний
Остановимся кратко на том, каким образом потребительские нормы и привычки влияют на форму траектории потребления. Во-первых, в условиях сформулированного утверждения объем потребления со временем сокращается, а имеющие место колебания происходят вокруг положительного линейного тренда, обладающего магистральным, притягивающим свойством (рисунок). Во-вторых, чем больше величина абсолютной антипатии к потреблению и чем ниже темп прироста агрегатной функции полезности, тем больше частота колебаний объема потребления. Это означает, что чем выше предельная полезность потребляемого блага и чем слабее выражен закон Госсена, тем неустойчивее потребительская стратегия, т. е. при низкой субъективной оценке блага экономический агент меньше склонен к «шараханию» в потреблении данного блага, период рождения потребительских флуктуаций растягивается и динамика x(t) имеет более стабильный характер. Кроме того, частота флуктуаций возрастает по мере увеличения социальной значимости альтернативного l-го блага по сравнению с i-м благом. В-третьих, чем больше абсолютная антипатия к потреблению и социальная значимость l-го блага, тем выше амплитуда экономических колебаний, т. е. чем выше предельная полезность блага и чем слабее; происходит насыщение спроса по мере потребления, тем больше размах колебательных тенденций в динамике потребления. В-четвертых, чем ниже темп прироста агрегатной функции полезности, тем медленнее происходит снижение объема потребления.
На наш взгляд, причина, вызывающая потребительские колебания, заключается в своеобразном, достаточно сложном, способе временного взвешивания (дисконтирования) экономическим агентом потока потребления. В качестве дисконтирующих коэффициентов выступают характеристики 1-го и 2-го порядков частной функции полезности, что и отражено в уравнении (5). Таким образом, потребительские циклы вызываются действием закона Госсена и аксиомы ненасыщения.
Если рассматривать упрощенный случай, когда имеет место только один товар, то стратегия потребления будет также описываться уравнением (5) при ω=0. В этом случае траектория потребления задается монотонно возрастающей функцией без экстремумов. Это означает, что процесс потребления является стабильным лишь в простейшем случае для п=1. При этом данный процесс чрезвычайно неустойчив и малейшее стороннее возмущение (появление ω=0) может вывести систему из стационарного режима, сбивая ее на детерминированные циклические колебания и ведя к перестройке фазового портрета уравнения (5). Таким образом, одна из основных причин образования потребительских флуктуаций – наличие множества благ. Именно действие дополнительных благ (не важно, комплементарных или взаимозаменяемых) и является тем «возмутителем спокойствия», который заставляет экономического агента придерживаться сложной динамики потребления.
Учитывая специфику конфигурации ω и то, что dUi/dUl = –pl/pi, отношение pl/pi представляет собой не что иное, как предельную норму замещения полезностей соответствующих видов потребительских благ. Следовательно, правомерно предварительное утверждение о том, что специфика дисконтирования потребления, отражаемая уравнением (5), является необходимым условием рождения экономических флуктуаций, а наличие нескольких благ, обладающих свойством взаимокомпенсирующей полезности, – достаточным условием.
Кратко остановимся на том факте, что решение (6) порождает два интересных парадокса. Первый связан с понижательным характером линейного тренда (магистрального луча) в условиях экспоненциального роста агрегатной полезности и линейного возрастания альтернативного блага, второй – с бифуркацией решения уравнения (5) при переходе от ω=0 к ω>0, когда монотонно возрастающая функция трансформируется в нисходящую траекторию с периодическими биениями. Прокомментируем данные эффекты.
Первый парадокс достаточно хорошо известен в экономической теории. Яркими примерами такого рода динамических эффектов являются теоремы Столпера–Самуэльсона и Рибчинского в форме Р.Джонса: у Рибчинского экзогенные изменения в темпах прироста объемов факторов производства приводят к непропорционально большим изменениям в объемах выпуска; у Столпера–Самуэльсона экзогенные изменения в темпах прироста товарных цен обусловливают более сильную реакцию цен макрофакторов [13]. Таким образом, в рассмотренной нами модели (5) имеет место, по сути дела, тот же эффект акселерации Р.Джонса, что и в простых малоразмерных моделях экономического равновесия.
Второй парадокс также хорошо изучен в различных разделах математики и прежде всего в теории бифуркаций. С точки зрения вариационного исчисления, динамического программирования и оптимального управления нетривиальная форма траекторий, обеспечивающих реализацию простых целевых установок, является также вполне естественным явлением. В качестве простейшей аналогии полученного результата можно привести способ движения корабля, следующего заданным курсом: борясь с различными подводными течениями и потоками ветра, капитан корабля вынужден лавировать вокруг заданной линии движения, постоянно отклоняясь от нее, что и приводит к волнообразной траектории пути следования судна.
Развитие модели. Генерация производственных циклов
Все полученные результаты достаточно наглядны, но, как указывалось выше, справедливы лишь для частного случая агрегатной функции полезности. В этой связи выполним некоторые важные обобщения. Для этого будем рассматривать, как и прежде, двухфакторную схему, где U=U[xi(t), xi(t)] – агрегатная функция полезности произвольного вида. В отличие от предыдущего случая, где функция полезности зависела лишь от объема потребляемых благ, здесь она зависит еще и от способа комбинации (вида взаимосвязи) этих благ. Иначе говоря, рассматриваемый случай позволяет в явном виде учесть возможные взаимодействия между факторами потребления. Тогда условия 1-го и 2-го порядков для функции полезности примут следующий вид:
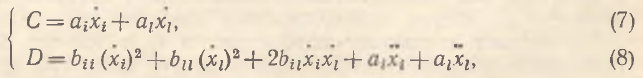
где 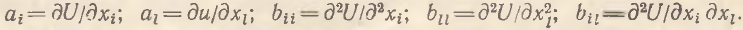
В соответствии с ортодоксальной теорией ai>0, аl>0 (аксиома ненасыщения), bii<0, bll<0 (закон Госсена), bij>0. При этом все показатели используются в канонической (классической) форме. Система (7) – (8), как и в предыдущем случае, редуцируется к уравнению
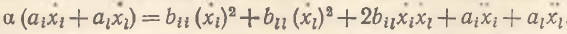 (9)
(9)
Теперь, как и ранее, примем ряд упрощающих обозначений и гипотез: r=const, ẋl=λ=const, .png) = –bii/ai – абсолютная антипатия к потреблению i-гo блага; θ=bil/аi, σ=bii/ai, µ=dxi/dxl – предельная норма замены i-го блага l-ым (в соответствии с принципом взаимозамещения µ<0); λ, θ, σ, µ и
= –bii/ai – абсолютная антипатия к потреблению i-гo блага; θ=bil/аi, σ=bii/ai, µ=dxi/dxl – предельная норма замены i-го блага l-ым (в соответствии с принципом взаимозамещения µ<0); λ, θ, σ, µ и .png) также являются константами. Тогда ẍl=0 и уравнение (9) принимает окончательный вид (индекс i для простоты опускаем):
также являются константами. Тогда ẍl=0 и уравнение (9) принимает окончательный вид (индекс i для простоты опускаем):
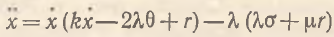 (10)
(10)
Несложно видеть, что уравнение (10) по структуре идентично уравнению (5); различие между ними состоит лишь в более сложной конфигурации параметров (10). Как и в уравнении (5), решение (10) бифурцирует к неустойчивому типу при нарушении условия
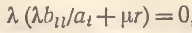 (11)
(11)
которое может трактоваться как условие отсутствия экономическикх колебаний (соответственно нарушение (11) – условие 1-го порядка неустойчивости экономического развития). Условие 2-го порядка для возникновения периодических флуктуаций в потреблении xi, задается бифуркационным неравенством
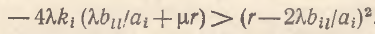 (12)
(12)
Анализ знаков фигурирующих здесь параметров показывает, что при λ>0 и r>0 левая часть (12) всегда больше нуля. Следовательно, строгое выполнение неравенства (12) отнюдь не тривиально и возможно лишь при определенном сочетании скоростных характеристик модели (10) и набора входящих в нее показателей эластичности. Несложно видеть, что, как и в случае модели (5), в (10) основным возмущающим фактором служит эффект замены двух благ. Таким образом, в модели (10) в явной форме фигурируют перекрестные эффекты взаимозамещения и комплементарности. Данные эффекты дополняются показателями bll и bil.
Рассмотренные динамические эффекты в сфере потребления могут быть распространены и на производственную сферу. В этом случае вместо потребительских благ xi и xl будут фигурировать традиционные макрофакторы – труд и капитал, понятие полезности (благосостояния) заменяется на выпуск продукции, а сама функциональная зависимость U=U[xi(t), xl(t)] превращается в обыкновенную производственную функцию. Поскольку уравнение (10) выведено для функций произвольного вида, то оно истинно и для таких зависимостей, как функция Кобба – Дугласа и CЕS–функция, традиционно используемых в макроанализе. Тогда в новой интерпретации r характеризует темп экономического роста, .png) означает абсолютную антипатию к использованию рассматриваемого макрофактора. При этом аксиома ненасыщения превращается в постулат о неотрицательной предельной производительности (эффективности) макроресурса, закон Госсена – в закон убывающей отдачи затрат, а принцип отрицательности нормы замены потребляемых благ – в принцип отрицательности предельной нормы замещения производственных факторов. Введенные предположения относительно стабильности коэффициентов в уравнении (10) содержательно означают отсутствие научно–технического прогресса.
означает абсолютную антипатию к использованию рассматриваемого макрофактора. При этом аксиома ненасыщения превращается в постулат о неотрицательной предельной производительности (эффективности) макроресурса, закон Госсена – в закон убывающей отдачи затрат, а принцип отрицательности нормы замены потребляемых благ – в принцип отрицательности предельной нормы замещения производственных факторов. Введенные предположения относительно стабильности коэффициентов в уравнении (10) содержательно означают отсутствие научно–технического прогресса.
Заметим, что двухфакторная модель (10) чрезвычайно удобна и информативна именно в производственных терминах. Так, например, для микроэкономической ситуации эффект возникновения эндогенных флуктуаций означает следующее. При постоянных во времени приростах инвестиций (для определенности анализа в качестве экзогенного фактора будем рассматривать именно этот производственный ресурс) достаточно активный стационарный рост производства фирмы возможен лишь при нестабильной динамике использования рабочей силы. Иными словами, стабильные капиталовложения приводят к устойчивому росту производства только при достаточно гибкой стратегии в отношении рабочей силы, выражающейся в оперативном избавлении фирмы от ее излишков и, наоборот, сверхбыстром восполнении появляющихся вакансий. Следовательно, стационарное расширение производственных возможностей фирмы возможно только благодаря высокой степени адаптируемости ко всем нюансам технологического процесса хотя бы одного из используемых ею макрофакторов. При этом в рассматриваемой теории фирмы, как и в теории потребления, одним из источников, провоцирующих эндогенные колебания, является эффект ненулевой эластичности замещения труда и капитала.
Понятно, что данные рассуждения аналогичны и для макрослучая, когда рассматривается стационарный рост всей макроэкономики. Если эндогенным фактором, как и ранее, рассматривать рабочую силу, то дихотомическое условие (12) характеризует режим возникновения циклов занятости. Следовательно, при определенной комбинации параметров (10) циклы занятости (а соответственно и безработицы) являются необходимым условием стабильного расширенного воспроизводства. В обратной ситуации, когда труд является экзогенным ресурсом, из уравнения (10) вытекает теория инвестиционных циклов, предполагающая неравномерность обновления и загрузки производственных мощностей. Кроме того, из (6) следует, что амплитуда циклических колебаний отнюдь не постоянна, а тяготеет к периодическим катастрофическим скачкам (рисунок). По-видимому, такие точки разрыва в кривой х(t) соответствуют периодам кризисов, когда производство и потребление сокращаются практически до нуля. В этой связи можно констатировать, что общая циклическая траектория расщепляется на «малые» (незначительные динамические флуктуации) и «большие» (кризисные спады) циклы.
Обобщенная теорема о рождении эндогенных флуктуаций
Рассмотрим теперь предельно общий многомерный случай, когда число потребительских благ (факторов) равно m. Тогда функция полезности (макропродукт) U=U(X), где X={xj, 1=m̅} и условия 1-го и 2-го порядков выглядят следующим образом:
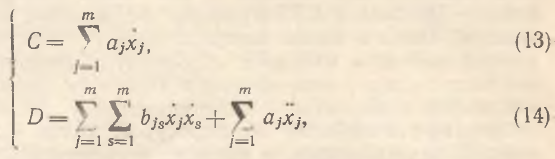
где 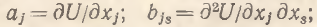 j и s – индексы потребляемых благ (производственных факторов). При прежних постулатах с учетом того, что ẋj=λj=const для всех
j и s – индексы потребляемых благ (производственных факторов). При прежних постулатах с учетом того, что ẋj=λj=const для всех 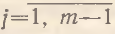 , искомая модель, описывающая динамику т-го блага (фактора), принимает вид
, искомая модель, описывающая динамику т-го блага (фактора), принимает вид
.png) (15)
(15)
Здесь, как и ранее, 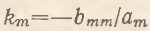 – абсолютная антипатия к потреблению (использованию) т-го блага (фактора);
– абсолютная антипатия к потреблению (использованию) т-го блага (фактора); 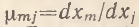 – предельная норма замены т-го блага (фактора) j-ым. Для удобства также введены обозначения
– предельная норма замены т-го блага (фактора) j-ым. Для удобства также введены обозначения
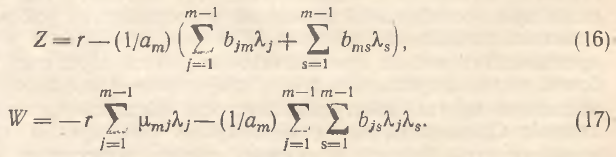
Уточненная таким образом модель позволяет сформулировать обобщенную теорему о рождении эндогенных флуктуаций в стационарно расширяющейся (сжимающейся) экономике.
Теорема: Если потребитель (производитель) потребляет (использует) т различных благ (факторов) таким образом, что т–1 из них изменяются постоянным темпом ẋj=λj, .png) , а динамика полезности (макропродукта) характеризуется постоянным темпом прироста r=U̇/U, то стратегия потребления т-го блага (фактора) при соблюдении условия 8
, а динамика полезности (макропродукта) характеризуется постоянным темпом прироста r=U̇/U, то стратегия потребления т-го блага (фактора) при соблюдении условия 8.png) mW>Z2 носит принципиально неустойчивый характер [14].
mW>Z2 носит принципиально неустойчивый характер [14].
Таким образом, при стационарном росте благосостояния потребителя (объема производства) и стабильном увеличении потребляемых благ (производственных факторов) при указанных условиях среди них всегда найдется хотя бы одно благо (один фактор), потребление (использование) которого будет подвержено стабильным, незатухающим флуктуациям [15]. Это означает также, что для моделируемой системы выполняется принцип взаимной динамической зависимости потребляемых благ (производственных факторов). Помимо этого, динамика каждого элемента хj зависит от широкого спектра перекрестных эластичностей. Учитывая зависимость динамики производства и потребления от особенностей движения цен, можно констатировать, что для моделируемого процесса характерна вальрасовская система цен, т. е. динамика каждой микроцены на потребительское благо (производственный ресурс) зависит от динамики всех остальных цен и показателей эластичности [16]. Данный факт является принципиальным, так как, во-первых, он полностью согласуется с классической теорией экономического равновесия, а во-вторых, данный результат получен исходя из методологических принципов, несколько отличающихся от тех, на которых базируется закон Вальраса [17]. Кроме того, следует отметить, что в рассмотренном случае имеет место явное усиление закона Вальраса, так как последний охватывает одновременно сферы производства и потребления, в то время как модель (15) отражает закономерности функционирования названных экономических секторов независимо друг от друга. Таким образом, вальрасовский принцип всеобщей взаимообусловленности пронизывает не только экономическую систему в целом, но и ее отдельные части. Организующим и синтезирующим началом подобной взаимосвязи между рассеянными в пространстве и времени потребительскими благами (производственными ресурсами) являются субъективные экономические интересы личности потребителя (производителя).
Уравнение (15) вместе с формулами (16) и (17) позволяет аккуратно классифицировать группы факторов, которые предопределяют характер динамики рассматриваемого блага (фактора). Методологически это означает рассмотрение возможности выполнения дихотомического условия 8.png) mW>Z2. В общем случае можно выделить шесть групп возмущающих воздействий.
mW>Z2. В общем случае можно выделить шесть групп возмущающих воздействий.
Первая группа – предельная полезность (производительность) αm. Для наиболее интересного случая, когда r>0 и λj>0, .png) , предельная полезность (производительность) оказывает, как правило, стабилизирующее воздействие на динамику хт. Это связано с тем, что при увеличении αm увеличивается значение возмущающего параметра W в модели (15), уменьшается абсолютная антипатия
, предельная полезность (производительность) оказывает, как правило, стабилизирующее воздействие на динамику хт. Это связано с тем, что при увеличении αm увеличивается значение возмущающего параметра W в модели (15), уменьшается абсолютная антипатия .png) m и возрастает Z. Такой эффект уменьшает вероятность выполнения условия, при котором возникают циклические колебания. Таким образом, рост αm способствует более целенаправленному поведению потребителя (производителя).
m и возрастает Z. Такой эффект уменьшает вероятность выполнения условия, при котором возникают циклические колебания. Таким образом, рост αm способствует более целенаправленному поведению потребителя (производителя).
Вторая группа – закон Госсена (закон убывающей отдачи затрат) – {bjj}. Данная группа факторов действует прямо противоположным образом первой группе факторов в отношении .png) m и Z и аналогичным образом в отношении W, тем самым дестабилизируя экономическую динамику и увеличивая разброс в действиях потребителей и производителей.
m и Z и аналогичным образом в отношении W, тем самым дестабилизируя экономическую динамику и увеличивая разброс в действиях потребителей и производителей.
Третья группа – перекрестные эффекты {bjs}, j≠s. Данный фактор уменьшает величину как W, так и Z. Таким образом, влияние рассматриваемых эффектов неочевидно. Однако учитывая квадратичную зависимость Z в соответствующем дихотомическом условии, по-видимому, они в большинстве случаев гасят возможные циклические колебания.
Четвертая группа – скорость разрастания рассматриваемой экономической системы (для макрослучая) или ее сегмента (для микрослучая) r. В большинстве случаев данный фактор по достижении некоторого порогового значения способствует более устойчивым тенденциям в развитии.
Пятая группа – скорость разрастания элементов рассматриваемой экономической системы (для макрослучая) или ее сегмента (для микрослучая) {λj}, .png) . О воздействии данной группы факторов в общем случае ничего нельзя сказать, так как все зависит от конкретных значений приростов и их комбинации между собой.
. О воздействии данной группы факторов в общем случае ничего нельзя сказать, так как все зависит от конкретных значений приростов и их комбинации между собой.
Шестая группа – принцип взаимозаменяемости потребительских благ (принцип взаимозаменяемости производственных факторов) {µтj;}. Чем сильней проявляется данный закон, тем больше W и, следовательно, тем выше вероятность рождения эндогенных флуктуаций. Данный вывод представляется наиболее интересным и важным, так как он по сути означает следующее: чем сильней эффект замены, тем сложней экономическая динамика. Такой результат полностью согласуется с основными положениями современной экономической теории.
Таким образом, рассмотренные группы факторов свидетельствуют о том, что их воздействие на динамику хт весьма неоднозначно и может быть сколь угодно разнообразным. Так, например, группы r и {λj} образуют своеобразные динамические потенциалы системы, которые балансируются достаточно сложным образом, в то время как первая, вторая, третья и шестая группы факторов представляют собой совокупность дисконтов, с помощью которых и происходит данная балансировка. При этом, как видно из уравнения (15), ускорение потребления ẍт и квадрат его скорости (ẋт)2 взвешиваются с помощью простых коэффициентов, которые не включают динамические характеристики других благ (факторов). Данный факт является вполне естественным, так как компоненты ẍт и (ẋт)2 отображают более тонкие эффекты (эффекты 2-го порядка) и лишь нивелируют возможный динамический дисбаланс. В этом смысле параметры при них образуют «медленную» составляющую системы дисконтов, в то время как параметры Z и W, аккумулируя в себе возмущения 1-го порядка, зависят от динамических факторов r и {λj} и образуют тем самым «быструю» составляющую.
В целом рассмотренные группы факторов позволяют уяснить себе, какие «силы» экономической системы, взаимодействуя и «борясь» между собой, приводят к новым сложным эффектам, иллюстрируя тем самым такое общее системное свойство, как эмерджентность. Тот же факт, что подавляющее большинство этих «сил» представляют собой универсальные законы и принципы экономической теории, свидетельствует о плодотворности используемого в данной работе подхода, продолжающего традицию современного маржинализма.
Остановимся теперь на бихевиористическом аспекте анализа. Дело в том, что рождение эндогенных колебаний происходит лишь при выполнении дихотомического условия 8.png) mW>Z2. В остальных режимах система обладает вполне удовлетворительной динамической устойчивостью. Логично задать вопрос: в какой степени поддержание динамической устойчивости системы является регулируемым процессом? Ответ на этот вопрос вытекает из проведенного анализа групп факторов, влияющих на характер дихотомии. В широком смысле слова регулированию подлежат все шесть групп, в узком смысле – параметры r и {λj}, так как первая, вторая, третья и шестая группы факторов в реальности слабоуправляемы и образуют комплекс псевдоэкзогенных социально–экономических условий, на фоне которых потребитель (производитель) реализует свои стратегии r и {λj}. Манипулируя именно объемами потребления {λj} и аккуратно подстраивая под них свои целевые установки в отношении темпа роста r, экономический агент может воздействовать на процесс в том или ином направлении. При этом практически всегда можно за счет более умеренного потребления некоторых благ (факторов) сохранять стационарность процесса. И наоборот, излишняя «жадность» в использовании некоторых благ (факторов) порождает циклы производства и потребления. Данные выводы несколько новы и неожиданны, пожалуй, лишь применительно к сфере потребления. Что касается производственной сферы, то относительно нее можно считать уже устоявшимся мнение о дестабилизирующем влиянии экономических «перегревов» на устойчивость экономического развития.
mW>Z2. В остальных режимах система обладает вполне удовлетворительной динамической устойчивостью. Логично задать вопрос: в какой степени поддержание динамической устойчивости системы является регулируемым процессом? Ответ на этот вопрос вытекает из проведенного анализа групп факторов, влияющих на характер дихотомии. В широком смысле слова регулированию подлежат все шесть групп, в узком смысле – параметры r и {λj}, так как первая, вторая, третья и шестая группы факторов в реальности слабоуправляемы и образуют комплекс псевдоэкзогенных социально–экономических условий, на фоне которых потребитель (производитель) реализует свои стратегии r и {λj}. Манипулируя именно объемами потребления {λj} и аккуратно подстраивая под них свои целевые установки в отношении темпа роста r, экономический агент может воздействовать на процесс в том или ином направлении. При этом практически всегда можно за счет более умеренного потребления некоторых благ (факторов) сохранять стационарность процесса. И наоборот, излишняя «жадность» в использовании некоторых благ (факторов) порождает циклы производства и потребления. Данные выводы несколько новы и неожиданны, пожалуй, лишь применительно к сфере потребления. Что касается производственной сферы, то относительно нее можно считать уже устоявшимся мнение о дестабилизирующем влиянии экономических «перегревов» на устойчивость экономического развития.
Нестационарный случаи с наличием экзогенных шоков
Выше рассматривалась стационарная экономика, для которой оказалось возможным построить вполне удовлетворительную теорию экономических флуктуаций. Однако условия стационарности, накладываемые прежде всего на такие динамически неустойчивые показатели, как α и ẋj, в реальности абсолютно невыполнимы. Тем не менее, как показал анализ, даже в стационарных условиях возможно возникновение циклических экономических колебаний. Именно в этом контексте имеет принципиальное значение сформулированная теорема о рождении эндогенных флуктуаций.
Что же касается вопроса о возможности построения общей теории для нестационарного случая, то на него можно дать отрицательный ответ. Так, например, если предположить, что все параметры в модели (15) изменяются во времени по каким-то своим собственным законам, то в этом случае динамика хт будет описываться уравнением
.png) (18)
(18)
Поскольку зависимость коэффициентов (18) от времени строго задана, то это равносильно наличию в системе экзогенных шоков (возмущений), которые и формируют эндогенную динамику xm(t).
Путем подстановки ẋт=ут уравнение (18) сводится к уравнению
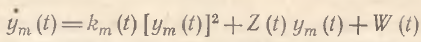 (19)
(19)
которое в теории известно как дифференциальное уравнение Риккати, в общем случае неразрешимое в квадратурах [18]. Данным фактом и обусловлена невозможность построения общей динамической теории экономических флуктуаций. Можно утверждать лишь то, что в подавляющем большинстве случаев интегральная кривая уравнения (18) будет иметь достаточно сложную форму с наличием локальных экстремумов, доказывая тем самым закономерный характер неравномерности динамики макро– и микропоказателей.
Как уже указывалось выше, модель (15) не учитывает в явном виде возможные ограничения; она содержит экзогенный вектор {λj}, который, однако, в реальности может включать отнюдь не любые значения. Действительно, постоянные во времени приросты т–1 благ (факторов) подразумевают, что потребитель (производитель) в соответствующие моменты времени может приобрести эти блага (факторы) в нужном количестве. Однако если эти приросты слишком велики, то такого количества благ (факторов) может не оказаться на товарном рынке (рынке ресурсов). Возможен случай, когда необходимые закупки могут быть произведены лишь с определенным запозданием. Не исключен также вариант, когда некоторые товары (ресурсы) устаревают (истощаются) и вообще исчезают с рынка. В этом случае каждая потребительская (производственная) стратегия может быть получена лишь с некоторой ненулевой вероятностью, что равносильно трансформации исходной агрегатной функции полезности (производственной функции) в функцию полезности фон Неймана–Моргенштерна и рассмотрению динамических потребительских лотерей (способов производства). Такие построения приводят уравнение (15) к стохастическому виду, в котором вероятностные оценки означают возможные нарушения экзогенных траекторий.
В данной работе не рассматривались также последствия возникающих эндогенных флуктуаций в сферах производства и потребления. Однако и без детального анализа ясно, что существование товаров, производство и потребление которых сильно осциллирует, в длительной перспективе не может не оказывать воздействия на остальные сегменты экономики. Такие возмущения, распространяясь по рыночным каналам связи, будут приводить к сбою в производстве и потреблении других товаров, захватывая все большее их число. В этом смысле товары с осциллирующими характеристиками производства и потребления образуют внутри системы своего рода ядро динамических флуктуаций, которое постоянно генерирует внутренние экономические шоки и тяготеет к детерминированному саморазрастанию. Это в свою очередь ведет к нарастанию в системе энтропии и увеличению нестационарности и стохастичности ее функционирования.
[1] См.: Милованов В.П. Об одном подходе к моделированию механизмов ценообразования//Экономика и мат. методы. 1994. Т. 30. Вып. 1.
[2] См.: Коровкин А.Г., Наумов А.В. Социально-экономические проблемы формирования рациональной занятости//Экономика и мат. методы. 1990. Т. 26. Вып. 5.
[3] См.: Поманский А.Б., Трофимов Г.Ю. Математические модели в теориях экономического цикла//Экономика и мат. методы. 1989. Т. 25. Вып. 5.
[4] См.: Дубовский С.В. Цикл Кондратьева как инновационно-экономический маятник с социальными последствиями//Экономика и мат. методы. 1994. Т. 30. Вып. 1.
[5] См.: Klein L.R., Preston R.S. Stochastic nonlinear models/Econometrica. 1969. Vol. 37. № 1; Балацкий E.В. Осциллирующие траектории в моделях динамики цен//Вестн. Моск. ун-та. Сер. Экономика. 1995. № 1.
[6] См.: Аукуционек С.П. Современные буржуазные теории и модели цикла. М., 1984.
[7] См.: Попов В.В. Экономический цикл и норма прибыли в США. М., 1989.
[8] См.: Вейцман М.Л. Модель синдрома дефицита//Экономика и мат. методы. 1990. Т. 25. Вып. 6.
[9] См.: Интрилигатор М. Математические методы оптимизации и экономическая теория. М., 1975.
[10] См.: Стиглер Дж., Беккер Г. О вкусах не спорят//США – экономика, политика, идеология. 1994. № 1–2.
[11] В узком смысле слова стационарной экономикой в нашем случае является экономика, в которой r=0; режим r>0 соответствует расширяющейся экономике, а состояние r<0 – коллапсирующей экономической системе. Здесь и далее без потери степени общности будем рассматривать случай расширяющейся экономики, который является наиболее репрезентативным.
[12] Доказательство данного утверждения тривиально и основывается на рассмотрении решения уравнения (5), соответствующего условиям утверждения. При интегрировании данного уравнения имеем (γ и β – постоянные интегрирования; ∆=4.png) ω–r2 – бифуркационная комбинация):
ω–r2 – бифуркационная комбинация):
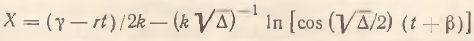 (6)
(6)
Таким образом, решением данного уравнения является квазипериодическая функция, что и требовалось доказать.
Может показаться, что утверждение о неравномерности потребления охватывает чрезвычайно узкий диапазон возможных случаев. Однако конфигурация ∆ свидетельствует, что это не так.
[13] См.: Линдерт П.X. Экономика мирохозяйственных связей. М., 1992.
[14] Аналитические условия выполнимости теоремы традиционны: функция U (•) является дважды дифференцируемой, имеет непрерывные частные производные и ее матрица Гессе отрицательно определена; все переменные хj попарно независимы (немультиколлинеарны) и дважды дифференцируемы по времени. Доказательство теоремы вытекает из анализа решений (15).
[15] В данной статье намеренно не рассматриваем альтернативный режим функционирования экономической системы, так же как и свойства сепаратрисы, для которой 8.png) mW=Z2.
mW=Z2.
[16] См.: Балацкий Е.В. О дискретном характере процесса ценообразования//Вестн. Моск. ун-та. Сер. Экономика. 1994. № 5.
[17] Из экономической теории известно, что в состоянии равновесия µmj= –pj/pm, где pj и рт – цены j-го и т-го товаров (ресурсов) соответственно. В этом случае относительные цены выступают в качестве возмущающего фактора в явном виде.
[18] См.: Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся вузов. М., 1986.
Официальная ссылка на статью:
Балацкий Е.В. Эндогенные флуктуации в расширяющейся экономике// «Вестник Московского университета. Серия 6, Экономика», №6, 1995. С.32–46.