Общие принципы моделирования динамики цен
На сегодняшний день можно констатировать отсутствие общей теории динамики цен, несмотря на то что экономико–математические и эконометрические разработки в данной области значительны. Оговоримся: в данной работе нас будут интересовать именно динамические свойства цен; – теоретические вопросы, связанные с формированием цен в статике не рассматриваются.
Рассмотрение динамики цен предполагает два аспекта. Первый из них связан с анализом переходных процессов в ценообразовании. При этом особое значение представляет факт дискретных переходов цен из одного состояния в другое [1]. Второй аспект проблемы связан с изучением направленности таких ценовых сдвигов на протяжении более длительных периодов времени. В этом случае дискретность ценообразования не имеет значения, и цена может восприниматься как непрерывная во времени функция, для которой в общем случае характерно наличие колебательных (волнообразных) тенденций. На рисунке схематично показана связь дискретных и волновых явлений в ценообразовании. Таким образом, для динамики цен характерен своего рода дискретно–волновой дуализм. В данной работе наше внимание будет сфокусировано на втором аспекте процесса ценообразования.
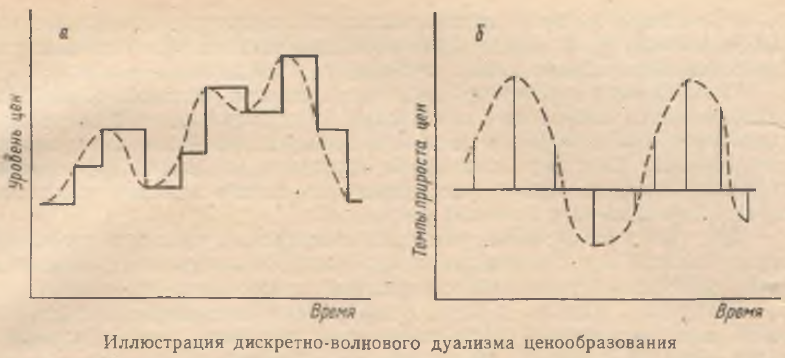
Основным положением исследований динамики цен является закон их изменения, вытекающий из теории равновесия. В самой общей постановке данный закон на понятийном уровне формулируется следующим образом: изменение цены на товар зависит от соотношения на рынке спроса и предложения. Используя понятие избыточного спроса, данное положение может быть несколько конкретизировано: изменение цены на товар зависит от состояния избыточного спроса. Именно такая обобщенная формулировка закона формирования цен является общепринятой. Конкретная же формализация данного положения весьма неоднозначна и связана с различными так называемыми схемами «нащупывания» равновесных цен [2].
Обобщенная модель «нащупывания» цен имеет следующий вид: ṗ=F[D(p)–S(p)], где р – цена анализируемого товара; D и S – спрос и предложение товара; F – оператор, задающий соответствие между величиной избыточного спроса и изменением цен. Как правило, спрос и предложение полагаются зависящими от цены. Такой подход позволяет с помощью одного уравнения описать основные поведенческие свойства экономической системы, включающей прямые и обратные связи (обратная связь замыкается именно через зависимости D(р) и S(p)). Однако понятно, что при использовании только одного уравнения движения цены описание процесса ценообразования является неполным, так как необходимо наличие по крайней мере еще двух уравнений, задающих в явной форме зависимость спроса (предложения) от цены. Именно в этом направлении возникает дополнительная проблема, без решения которой не удается построить полную и непротиворечивую теорию динамики цен.
Помимо неоднозначности функциональной связи между изменением цены и избыточным спросом инструментальная трудности при моделировании ценообразования осложняется тем, что в отношении обратной зависимости между спросом (предложением) и ценой также не существует достаточной ясности. Наиболее простой и часто используемый подход в данном случае предполагает линейные зависимости вида: D=mp+m*; S=np+n*, где т, п, т* и п* – структурные параметры [3]. Философия такого подхода основана на представлении о том, что все реальные процессы линейны в малом. Однако в реальности довольно часто возникают специфические эффекты, которые не вписываются в жесткие рамки линейных конструкций. Например, из приведенных зависимостей следует, что ∂D/∂p=m. Если т<0 и m=const, то имеем описание естественного случая, когда анализируемый товар является обыкновенным; существование же так называемого гиффиновского эффекта, когда ∂D/∂p>0, противоречит полученному следствию. Таким образом, использование линейной формы связи соответствует существенному огрублению и искажению действительности, так как, во-первых, потеря гиффиновских эффектов недопустима в силу их чрезвычайной важности, а, во-вторых, чувствительность спроса по цене во все периоды времени предполагается одинаковой, что практически исключено и не имеет экономического смысла. Аналогичные рассуждения справедливы и для зависимости «предложение–цена».
По-видимому, при построении теоретических моделей ценообразования попытки построения конкретных видов зависимостей экономического типа между спросом (предложением) и ценой являются нецелесообразными. Поэтому ниже будем изучать предельно общие модели, в рамках которых можно рассмотреть поведение цен для различных типов товаров на качественном уровне.
Для того чтобы рассмотреть динамические свойства цен различных» групп товаров при построении и верификации конкретных модельных схем, необходимо учитывать следующие методические принципы.
Во-первых, модель должна генерировать следующие виды траекторий цен: монотонный рост, монотонное снижение, стационарный и колебательный режимы. Во-вторых, осциллирующие тенденции в общем случае должны иметь иррегулярный характер, так как наблюдаемые в реальности колебания весьма далеки от строго периодических. В-третьих, возникающие в системе эндогенные колебания цен должны предусматривать возможности к затуханию, нарастанию и самоподдерживанию. В-четвертых, колебательные движения цен в общем случае могут обладать тремя видами трендов: понижательным, повышательным и стационарным.
Идеальная теоретическая модель динамики цен должна соответствовать всем четырем положениям одновременно. Только в этом случае модельное отображение может претендовать на удовлетворительную адекватность реальным процессам.
Классификация товаров
Очевидно, что для различных типов товаров характерны различные траектории цен, свидетельствующие о неодинаковой степени их динамической устойчивости. Так, например, трудно предположить, что для нормального и гиффиновского товаров динамика цен будет одинаковой, даже если спрос и предложение на них будут изменяться абсолютно синхронно. В этой связи дадим классификацию товаров в зависимости от характера реакции спроса и предложения на цены (таблица 1).
Таблица 1. Классификация товаров
|
Реакция предложения |
Реакция спроса |
|
|
нормальные товары |
товары Гиффина |
|
|
Прибыльные товары |
I традиционные товары |
II перспективные товары |
|
Неприбыльные товары |
III неперспективные товары |
IV псевдоперспективные товары |
Разумеется, названия товаров, фигурирующие в таблице, носят условный характер. Эффекты, связанные с переключением спроса при изменении цены, достаточно хорошо изучены. В связи с этим прокомментируем лишь эффекты, связанные с переключением предложения. Так, например, случай ∂S/∂p>0 соответствует стандартной ситуации, когда увеличение цены приводит к росту прибыли у производителя, что и стимулирует рост производства, а следовательно, и предложения. Если же ∂S/∂p<0, то это может означать следующее: либо данный товар является «отмирающим», который вытесняется с рынка более новыми и прогрессивными заменителями (товары, попадающие в квадрант III); либо дальнейшее производство данного товара сопряжено с ростом издержек (например, из-за истощения соответствующих сырьевых рынков и удорожания факторов производства) и снижением прибыльности (группа товаров IV квадранта); либо данный товар придерживается торговыми дилерами, которые ожидают дальнейшего еще большего роста цены (товары IV квадранта). В качестве особого товара можно рассматривать ценные бумаги, предложение которых подчиняется весьма сложным законам. В частности, довольно хорошо известны случаи использования иррациональных стратегий инсайдерами на рынке капиталов. Так, например, аномальные эффекты в предложении ценных бумаг могут порождаться возникающими на рынке капиталов информационными «шоками», когда искажения истинной информации, прокатываясь по всем участкам торгов, приводят к псевдооптимальному поведению инсайдеров [4].
Таким образом, комбинация возможных стратегий в поведении потребителя и производителя дает возможность систематизировать товары на 4 группы, для каждой из которых характерны свои особенности динамики цен.
Линейные модели динамики цен
Наиболее простым случаем линейных систем «нащупывания» цен является модель, предложения П.Самуэльсоном: ṗ=ω[D(p)–S(p)], где ω>0 – структурный параметр, характеризующий скорость адаптации цен на несбалансированность спроса и предложения [5]. При параметризации показателей чувствительности спроса и предложения к изменениям цены, т.е. ∂D/∂p=α и ∂S/∂p=β, модель П.Самуэльсона преобразуется к уравнению
p̈ + (β–α) ωṗ = 0 (1)
решением которого является экспоненциальная траектория р=А+Вехр(α–β) ωt/, где t – время; А и В – постоянные интегрирования, зависящие от начальных условий.
Уравнение (1) имеет преимущество по сравнению с исходной моделью П.Самуэльсона в том смысле, что позволяет исследовать динамические свойства цен различных типов товаров, указанных в таблице. Рассмотрим подробнее возможные случаи.
Так, например, из уравнения (1) видно, что траектория p(t) непосредственным образом не зависит от соотношения спроса и предложения. Данный факт уже сам по себе является весьма ценным. Например, из модели П.Самуэльсона следует, что цена остается неизменной лишь в случае сохраняющегося равновесия на товарном рынке, в то время как из (1) вытекает, что независимо от конкретной величины избыточного спроса цена, как оказывается, может обладать свойством стационарности. Для этого достаточно, чтобы величины потенциальной чувствительности спроса и предложения по цене совпадали и были постоянными во времени: α=β=const. Таким образом, динамика цены оказывается зависимой от обратной реакции спроса и предложения на ценовые сдвиги. Тем самым цена, спрос и предложение изменяются одновременно в едином динамическом режиме.
Понятно, что цена р=А+В в данном случае отнюдь не обязательно является равновесной ценой. Учитывая причинно–следственную взаимозависимость характеристик р, S и D, рассмотренный случай в реальности соответствует такой ситуации, когда какое-либо произвольное изменение цены приводит к однонаправленным одинаковым по величине сдвигам в объемах спроса и предложения, в результате чего система попадает в устойчивое стационарное состояние. Нарушиться последнее может лишь из-за внешних возмущающих воздействий или при изменении чувствительностей α и β. Заметим, что анализируемый случай соответствует товарам из II и III групп таблицы и является маловероятным, так как величины α и β, вообще говоря, тяготеют к разнонаправленное. Тем не менее рассмотрение такого переходного процесса имеет определенное значение.
Теперь рассмотрим случай, наиболее характерный для конкурентной экономики, когда анализируемый товар соответствует I группе таблицы. Оказывается, в этом случае для цены характерна устойчивая тенденция, к снижению, причем ее нижней асимптотой является величина р=А, которая, по-видимому, может интерпретироваться в качестве себестоимости товара, ниже которой цена не может упасть. Данный результат представляется весьма сильным, ибо он приводит к утверждению, что в нормальных условиях цена на традиционный товар имеет объективную тенденцию к снижению. В условиях постоянства издержек производства данный процесс соответствует снижению удельной нормы прибыли производителя. Понятно, что полученный результат имеет смысл лишь для небольших временных интервалов, когда параметры чувствительности спроса и предложения по цене неизменны.
Прямо противоположная ситуация характерна для товара IV группы. В этом случае цена имеет повышательную тенденцию, которая ничем не ограничена. Такое положение представляется достаточно естественным, так как увеличение цены в силу специфической реакции системы приводит к росту рассбалансированности спроса и предложения, что в свою очередь оказывает на нее повышательное воздействие. Подобный механизм действия положительных прямых и обратных связей между ценой и избыточным спросом возможен лишь в весьма специфических условиях. В частности, данный механизм настройки цен действует в период стагфляции (гиперинфляции).
Два других случая уже менее однозначны. Так, например, для товара группы III цена неограниченно возрастает, если |α|>|β| и убывает при |α|<|β|. Для товара группы II цена имеет повышательный тренд при |α|>|β| и понижательный при |α|<|β|. Полученные результаты адекватны простейшим экономическим процессам и соответствуют эмпирическим наблюдениям относительно поведения цен.
Таким образом, рассмотрение возможных типов траектории цен уравнения (1), а следовательно, и модели П.Самуэльсона, Позволяет сделать следующие выводы. Наиболее вероятным типом для динамики цен является монотонная тенденция к убыванию, которая реализуется в естественных экономических условиях. Менее вероятней' является тенденция к росту цен, так как условия, обеспечивающие такую динамику, соответствуют более специфическим экономическим эффектам. Еще менее вероятным для динамики цен оказывается стационарный режим.
К числу недостатков модели (1) следует отнести тот факт, что она выпускает из рассмотрения чрезвычайно важный динамический вариант, связанный с возможными колебаниями цен. Учитывая, что осциллирующие тенденции могут быть как экзогенными, так и эндогенными, модель (1) принципиально не способна порождать именно эндогенные циклы. Что касается экзогенных возмущений, то их можно ввести двумя способами.
Первый способ связан с введением в правую часть уравнения (1) возмущающей функции G(t). Тогда решения (1) будут деформироваться и, в частности, могут иметь колебательную природу. Исходная модель П.Самуэльсона в этом случае будет трансформироваться к стохастическому виду ṗ=ω[D(p)–S(р)]+ʃG(t)dt. Учитывая, что G(t) – случайный процесс (белый шум), модель (1) может иметь достаточно естественную экономическую интерпретацию: помимо детерминированного формирующего фильтра ω(D–S) на динамику цен могут оказывать влияние случайные факторы, в качестве которых могут выступать ожидания будущих изменений, цен, спроса и предложения; действие торговых барьеров на микрорынках; политические инциденты типа войны в Персидском заливе; проведение государством фискальных рестрикций; дезинформация на экономических рынках и т.п.
Второй способ связан со снятием нереалистичной гипотезы о постоянстве чувствительности спроса и предложения по ценам, которая использовалась лишь в аналитических целях. В этом случае в уравнении (1) коэффициенты аир зависят от времени и экзогенное задание их траекторий позволяет проводить чрезвычайно интересные численные эксперименты по изучению их возмущающего воздействия на характер движения цены. Понятно, что последняя может осциллировать каким угодно образом – как строго циклически, так и апериодически.
Линейно–интегральные модели динамики цен
Одним из подходов к моделированию динамики цен являются линейно-интегральные схемы нащупывания. Частным и вместе с тем достаточно общим случаем такого подхода является модель Ф.Дреша [6]:
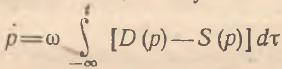
Основным отличием модели Ф.Дреша от модели П.Самуэльсона является учет всей предшествующей информации о динамике спроса и предложения при формировании цены. В этом смысле модель Ф.Дреша улавливает имеющиеся временные лаги в реакции системы на изменяющуюся величину избыточного спроса. Несложно видеть, что модель Ф.Дреша является естественным обобщением модели П.Самуэльсона; последняя предполагает «схлопывание» всей ценовой информации до точки текущего момента времени. Однако, на наш взгляд, модель Ф.Дреша также имеет ряд недостатков. Во-первых, в соответствии с современной экспектационной теорией цена должна зависеть не только от прошлых, но и от будущих изменений спроса и предложения. Во-вторых, бесконечный нижний предел интегрирования является определенной идеализацией, так как экономические агенты учитывают ситуацию за ограниченный ретроспективный период. В этой связи бесконечные пределы интегрирования могут быть заменены на конкретные параметры, характеризующие горизонт прошлых и будущих периодов, учитываемых при ценообразовании. Более того, в реальности величина таких периодов является весьма незначительной и существенно различается в зависимости от вида товара. Так, например, для группы товаров длительного пользования продолжительность указанных периодов, вероятно, больше, чем для группы товаров с коротким жизненным циклом. Учитывая сказанное, модель Ф.Дреша может быть обобщена следующим образом:
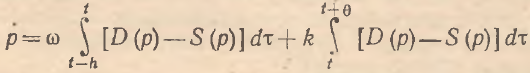 (2)
(2)
где 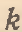 структурный параметр, аналогичный ω; h и θ – соответственно ретроспективный и перспективный периоды, учитываемые при ценообразовании.
структурный параметр, аналогичный ω; h и θ – соответственно ретроспективный и перспективный периоды, учитываемые при ценообразовании.
Преобразуем модель Ф.Дреша к более удобному для нашего анализа виду: p̈=ω[D(p)–S(р)]. Сравнение данного уравнения и модели П.Самуэльсона позволяет выявить их принципиальное различие с несколько иной стороны. Так, если в модели П.Самуэльсона дисбаланс на товарном рынке в конкретный момент времени определяет изменение цены (или ее скорость), то в полученной модификации модели Ф.Дреша имеющийся избыточный спрос влияет на скорость этого изменения (или на ускорение движения цены). Заметим, что к аналогичной модификации модели Ф.Дреша приводит также следующая обобщенная линейно–интегральная модель: ṗ=ω∫[D(р)–S(p)]dt. Дополнительные преобразования исходной схемы Ф.Дреша приводят к следующему уравнению:
 (3)
(3)
Здесь как и в уравнении (1) динамика цены не зависит непосредственным образом от соотношения спроса и предложения. Характеризуя конкретные случаи, отметим, что свойством стационарности цена в модели (3) обладает при тех же условиях, что и в (1): при α=β. Для перспективных и неперспективных товаров (группы III и II) характерна монотонная экспоненциальная траектория цены при α–β>0 (конкретное направление кривой цен, вверх или вниз, зависит от значений постоянных интегрирования). Динамике цен псевдоперспективных товаров (группа IV) также присуща гладкая тенденция независимо от конкретных значений α и β. Для остальных же случаев и прежде всего для наиболее репрезентативного варианта традиционных товаров (группа I) характеристические корни уравнения (3) оказываются комплексными, и формула цены имеет вид синусоиды, т. е. цена подвержена периодическим колебаниям.
Таким образом, в естественных условиях для цены обыкновенного товара характерны регулярные колебания. Данное положение противоречит следствию, вытекающему из уравнения (1). Следовательно, исходные модели П.Самуэльсона и Ф.Дреша по-разному описывают движение цен на различные группы товаров. Простейшие эвристические рассуждения приводят к выводу о большей реалистичности уравнений (3) по сравнению с (1). Кроме того, исходная модель Ф.Дреша, на которой базируется уравнение (3), генерирует эндогенные колебания цен, что отсутствует в альтернативной модели (1). Тем самым линейно-интегральная схема формирования цен описывает реальную экономическую динамику более полно, чем линейная схема.
Учитывая, что в экономических исследованиях большое внимание уделяется выявлению механизмов; индуцирующих возникновение циклических колебаний в системе, целый ряд вопросов может сниматься путем идентификации так называемых эндогенных циклов. В этом смысле линейно-интегральная модель (3) имеет достаточно большое значение, так как из нее следует, что для колебательных тенденций в динамике цены достаточно, чтобы зависимость ее изменений от величины избыточного спроса предусматривала временные распределенные запаздывания (упреждения).
Для привнесения в уравнение (3) экзогенных флуктуаций допустимы те же два подхода, что и при работе с уравнением (1).
Некоторые нелинейные схемы формирования цен
Проводимые экономические исследования показывают, что подавляющее большинство экономических зависимостей имеет нелинейный характер. В связи с этим можно предположить, что взаимосвязь между изменениями цен и объемами спроса и предложения также является не столь простой, как это предполагается в линейных и линейно–интегральных моделях.
Одной из простейших нелинейных схем является модель, в которой скорость изменения цены зависит не от абсолютной величины избыточного спроса, а от относительного дисбаланса на товарном рынке [7]: ṗ=ω[D(p)/S(р)–1]. Полагая величины чувствительности спроса и предложения постоянными и сохраняя прежние обозначения, данная модель может быть сведена к уравнению: (S/ω)р̈+(βD/S–α)ṗ=0. Однако даже столь простое уравнение нельзя полностью параметризовать в силу априорной подвижности спроса и предложения. Единственной возможностью поддерживания величин S и D на неизменном уровне является их полная нечувствительность к изменениям цены. Таким образом, исходная модель оказывается весьма неудобной для аналитического исследования.
Рассмотрим теперь модели, описывающие восстановительный процесс нащупывания цен. В соответствии с данным подходом силы, стремящиеся вернуть систему в состояние равновесия, обладающее своеобразным «притягивающим» свойством, напряжены тем больше, чем значительнее расхождение между заданным и равновесным состояниями системы [8]. Таким образом, темпы восстановительного процесса должны замедляться по мере приближения к равновесной цене. В этом случае вместо характеристики скорости изменения цен в моделях используется показатель темпа прироста. Так, например, в соответствии с принципом восстановления модель П.Самуэльсона может быть сведена к следующему нелинейному виду: ṗ/p=ω[D(р)–S(р)]. Такая модель эквивалентна дифференциальному уравнению
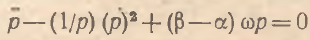 (4)
(4)
По составу параметров уравнение (4) достаточно удобно, однако его формальная сложность существенно ограничивает заложенные в нем аналитические возможности.
Применительно к линейно–интегральной модели принцип восстановления приводит к следующей конструкции: 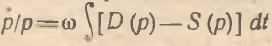 , которая равносильна уравнению
, которая равносильна уравнению
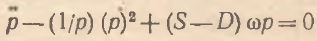 (5)
(5)
Если полагать, что в данном уравнении величины S и D принудительно поддерживаются на неизменном уровне, то можно рассмотреть долговременное воздействие избыточного спроса на динамику цен. Тем не менее аналитические возможности такой модельной схемы также весьма незначительны.
Представленная выше структурно–нелинейная модель предполагает многочисленные модификации. Например, ṗ=ω[1–S(p)/D(p)]. Кроме того, возможно рассмотрение ее интегрального аналога. Дополнительное усложнение таких модельных разновидностей дает принцип восстановления. Механизм анализа подобных модельных схем идентичен рассмотренным выше случаям.
Таким образом, рассмотренные нелинейные модели оказываются значительно сложнее линейных схем, не давая при этом заметных преимуществ в расширении аналитических возможностей. Из приведенных уравнений наиболее приемлемыми представляются (4) и (5). По-видимому, в идеале динамика цены должна описываться нелинейным дифференциальным уравнением третьей степени [9], включающем в качестве параметров показатели α и β; величины D и S в явной форме должны отсутствовать. Лишь в этом случае могут продуцироваться, эндогенные колебания иррегулярного типа, предполагающие различные частные случаи в зависимости от комбинаций α и β.
Синтетические модели ценообразования
Как указывалось выше, все рассмотренные модельные механизмы ценообразования предполагают определенные комбинации при их синтезе. Ниже рассмотрим простейшую модель, основанную на синтезе линейной и линейно–интегральной схем формирования цены:
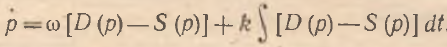 (6)
(6)
Такой механизм нащупывания цен соответствует представлению о том, что изменение цены зависит как от кумулятивного избыточного спроса, так и от величины избыточного спроса в рассматриваемый момент времени. Причем влияние каждого фактора неодинаково, что и показывают коэффициенты ω и .png) . Модель (6) позволяет перейти к следующему уравнению динамики цен:
. Модель (6) позволяет перейти к следующему уравнению динамики цен:
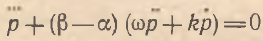 (7)
(7)
Несложно видеть, что структура решения уравнения (7) сложнее, чем для линейных и линейно–интегральных моделей. Так, например, траектории цен в (7) могут иметь как монотонно–экспоненциальный, так и колебательный характер. При этом из анализа характеристических корней уравнения (7) вытекает, что тип траектории цен напрямую зависит от значений эластичности α и β. Причем периодические колебания наблюдаются лишь при выполнении следующего дихотомического условия: α<β<α+4.png) /ω2. Данное условие характеризует диапазон возможных значений β при заданном α, который ограничивается полосой
/ω2. Данное условие характеризует диапазон возможных значений β при заданном α, который ограничивается полосой 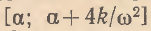 (
(.png) >0, ω>0) и обеспечивает циклические колебания цен. Заметим, что в отличие от линейной и линейно–интегральной схем ценообразования характер решения (7) непосредственным образом зависит от скоростных параметров модели ω и
>0, ω>0) и обеспечивает циклические колебания цен. Заметим, что в отличие от линейной и линейно–интегральной схем ценообразования характер решения (7) непосредственным образом зависит от скоростных параметров модели ω и .png) . В случае попадания β в область, очерченную приведенным выше дихотомическим условием, динамическое уравнение цены имеет вид
. В случае попадания β в область, очерченную приведенным выше дихотомическим условием, динамическое уравнение цены имеет вид
 (8)
(8)
где 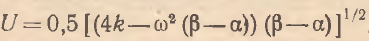 .
.
Как видно из (8), решение исследуемой синтетической модели имеет экспоненциальный мультипликатор, который определяет затухание или расхождение колебаний в зависимости от комбинации величин чувствительности спроса и предложения по ценам. В частности, для традиционного товара I группы при выполнении дихотомического условия цена подвержена затухающим циклическим колебаниям, т. е. такое сочетание эластичностей оказывает стабилизирующее влияние на колебания цены. Таким образом, в естественных условиях цена тяготеет к некоему состоянию равновесия, которое в рассматриваемом случае является устойчивым. При тех же условиях, но при наличии гиффиновского эффекта (α<0) положение не изменяется, если данный эффект проявляется недостаточно сильно, т. е. α–β<0. Сильный гиффиновский эффект, когда α–β>0, дестабилизирует положение равновесия, генерируя нарастающие колебания в динамике цены.
Если помимо основных сил, действующих на товарном рынке (спроса и предложения), в экономической системе имеются какие-либо внешние воздействия, то за счет введения возмущающей функции G(t), которая в данном случае отнюдь не обязательно имеет стохастическую природу, уравнение (7) превращается в неоднородное дифференциальное уравнение. В этом случае, как известно, в динамике цен могут возникать еще более сложные эффекты. В частности, если внешняя сила подвержена периодическим колебаниям, то при определенных условиях в системе могут возникать резонансные эффекты, которые приводят к росту амплитуды колебаний цены, что негативно сказывается на функционировании товарного микрорынка. Возможно также возникновение так называемых биений в динамике цены [10]. В этой связи интересен следующий факт: несмотря на то что биения имеют периодическую природу, экономическими агентами они могут восприниматься как неупорядоченные флуктуации. При субъективности восприятия такого явления и при хаотической смене комбинаций параметров модели α и β возникает динамический процесс, эквивалентный существованию иррегулярных колебаний. Таким образом, модель (6) более полно охватывает возможные ценностные эффекты и, следовательно, более адекватно отражает реальные экономические процессы по сравнению с рассмотренными ранее модельными схемами.
Полученные результаты не исчерпывают аналитических возможностей сконструированной нами модели (6). Однако более детальное обсуждение свойств решений уравнения (7) и всех возможных комбинаций α и β нецелесообразно в виду их громоздкости.
Несмотря на то что возможны и другие многочисленные случаи синтетических моделей динамики цен, по-видимому, наиболее простой и содержательной является рассмотренная модель (6).
Динамическое агрегирование цен
Выше были получены динамические уравнения микроцен для конкретных механизмов нащупывания конкурентного состояния равновесия. Данные результаты являются частными случаями так называемой «паутинообразной» схемы ценообразования. Их ценность достаточно высока, так как в реальности товарный макрорынок сегментирован на множество микрорынков, каждый из которых в результате игры спроса и предложения порождает свои собственные траектории цен, которые, «переплетаясь» между собой, определяют характер движения совокупного уровня цен и воздействуют на эмиссионный процесс. В теоретических и статистических исследованиях указанный феномен порождает чрезвычайно сложную проблему агрегирования микроцен. Сущность данной проблемы состоит в оценке агрегатного индекса цен и анализе его тенденций, без чего невозможно корректное исследование динамики экономического роста. При этом используется процедура «сжатия» имеющейся информации о движении микроцен с помощью определенных весовых коэффициентов. Данная проблема агрегирования цен не имеет общего решения, несмотря на многочисленные подходы, позволяющие в той или иной мере приблизиться к нему.
Ниже мы дадим лишь возможную экономико–математическую трактовку весовых коэффициентов, используемых при динамическом агрегировании цен. Для этого инвертируем традиционную постановку задачи следующим образом. Если совокупный индекс цен и его динамика определяются величинами и динамикой микроцен, то что представляют собой весовые коэффициенты, с помощью которых происходит «свертка» цен микрорынков? Действительно, всегда существует некий совокупный индекс (уровень) цен P(t), который аккумулирует все ценовые характеристики микрорынков pi(t), где i – индекс микрорынка (товары), так что в общем виде зависимость между ними задается тривиальным тождеством
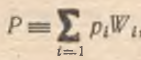 (9)
(9)
где Wi – весовые агрегирующие коэффициенты, i=1̅,̅I̅.
Для конкретизации дальнейшего анализа рассмотрим, простое тригонометрическое агрегирование, т. е. агрегирование осциллирующих цен, которые задаются динамическими уравнениями, являющимися решениями (3). В этом случае тождество (9) перепишется следующим образом:
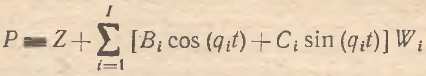 (10)
(10)
где qi=[βi–αi)ωi]1/2 – частотная характеристика, α параметр Z представляет собой своеобразный масштабирующий коэффициент и отражает автономные эффекты в динамике микроцен типа условно–постоянных издержек производства. Иными словами, компонент Z задает базовый уровень совокупного индекса цен (математическое ожидание), вокруг которого происходят колебания. Тогда второй компонент (10) отражает непосредственно динамические эффекты в динамике P(t). На наш взгляд, идентификация весовых коэффициентов актуальна в основном именно для динамической составляющей совокупного уровня цен Р(t). Рассмотрим их возможный вид.
Если переобозначить амплитудные параметры bi=WiBi, ci=WiCi, b0/2=Z, аргументы тригонометрических функций, входящие в (10), переписать в виде qi=πqi*/T, где Т – период исследования динамики цен, и использовать гипотезу о практической необозримости микрорынков, т. е. I→∞, то уравнение (10) преобразуется к квазитригонометрическому ряду Фурье. Если же все гармоники полученного ряда проранжировать в порядке возрастания, то получим канонический вид ряда Фурье:
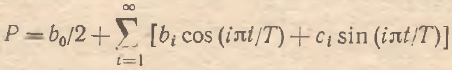 (11)
(11)
На наш взгляд, переход к (11) вполне правомерен, так как, учитывая бесконечное множество ценовых гармоник, «разбросанных» по различным частотам, их всегда можно упорядочить таким образом, чтобы получить ряд (11).
Хорошо известно, что для того чтобы разложение (11) существовало, параметры αi, и bi должны представлять собой коэффициенты Фурье. Однако определение весовых коэффициентов динамической составляющей P(t) независимо от его автономного компонента может привести к тому, что подстановка полученных значений агрегирующих коэффициентов нарушит равенство (11). Для этого необходимо скорректировать все коэффициенты на константу о (существование такой константы не требует специального доказательства). Учитывая также введенные нормирующие условия Wi=biBi=ciCi, получаем, что искомые весовые коэффициенты Wi представляют собой также некие аналоги коэффициентов Фурье:
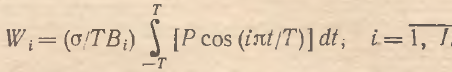 (12)
(12)
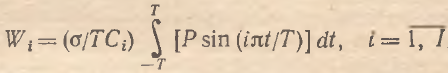 (13)
(13)
Автономный компонент в общем случае имеет вид
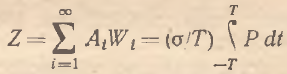 (14)
(14)
Из полученных зависимостей вытекает достаточно интересная интерпретация агрегирующих коэффициентов, которая позволяет сделать следующие качественные выводы.
Во-первых, весовые коэффициенты напрямую зависят от величины временного интервала, на котором анализируются ценовые эффекты. Следует иметь в виду, что данное утверждение является истинным лишь для абсолютных значений коэффициентов. Во-вторых, величина агрегирующих коэффициентов зависит от частоты и амплитуды колебаний микроцены. Такой вывод представляется достаточно интересным и неожиданным, так как в традиционном понимании «вклад» микроцены в макроценовую динамику зависит от «мощности» соответствующего микрорынка, которая в свою очередь определяется его товарной емкостью. В данном же случае оказывается, что «вес» микроцены зависит от ее собственных динамических свойств, а не от объемных характеристик микрорынка. Из (12) и (13) следует также, что чем больше амплитуда колебаний микроцен, тем меньше величина их агрегирующих коэффициентов. Иными словами, наиболее существенное влияние на формирование динамики совокупного уровня цен оказывают именно те микрорынки, которые характеризуются незначительными колебаниями своих ценовых параметров. Из (14) следует, что чем больше абсолютный уровень микроцен, тем меньше величина агрегирующих коэффициентов, т. е. по мере возрастания уровня микроцен относительная значимость их динамических свойств для динамики совокупного уровня цен постепенно нивелируется. Другими словами, данный вывод означает, что чем выше цены на товарных микрорынках, тем менее гибко реагирует экономическая макросистема на их изменения.
Теперь покажем, что использованное выше тригонометрическое агрегирование, вообще говоря, является достаточно общим случаем динамического агрегирования цен. Для этого достаточно свести монотонные экспоненциальные траектории к тригонометрическим функциям.
Это можно сделать с помощью разложения экспоненты в ряд Фурье. Так, например, решение (1) в этом случае принимает вид [11]
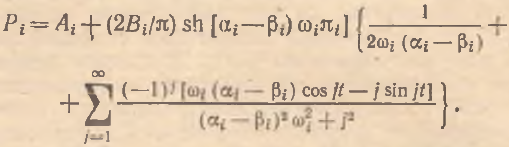 (15)
(15)
Из (15) видно, что помимо гармонической составляющей микроцена включает еще гиперболический мультипликатор, который можно внести под знак суммы и в результате процедур преобразования, переобозначения и ранжирования при макроагрегировании можно получить обыкновенный ряд Фурье с содержательными выводами, аналогичными случаю тригонометрического агрегирования.
Учитывая возможность, разложения в ряд Фурье любой монотонной функции, имеем достаточно элегантное формальное объяснение того факта, что при крайне неустойчивой динамике микроцен могут наблюдаться весьма гладкие тенденции совокупного индекса цен, выражающиеся в плавном экономическом росте и денежно–кредитной стабильности.
В заключение покажем, как соотносятся между собой агрегирующие коэффициенты Wi и объемные характеристики микрорынков. Для этого запишем очевидное агрегирующее тождество
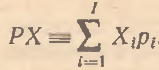 (16)
(16)
где Xi – объем i-го товарного микрорынка в натуральном выражении. Понятно, что (16) истинно как для переменных спроса D и Di, так и для переменных предложения S и Si. Из (16) следует, что
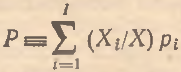 (17)
(17)
Таким образом, из сравнения (17) и (9) ясно, что весовые коэффициенты определяются объемными характеристиками: Wi=Xi/X. Однако величина X является не менее абстрактной, чем Р, так как предполагает своеобразное «слияние» всех разнородных и несопоставимых товаров в единую характеристику товарной массы. Очевидно, что уже само по себе такое «слияние» возможно только в ценовых терминах, что и определяет зависимость агрегирующих коэффициентов от динамических свойств микроцен.
Отметим, что существуют и другие подходы к построению совокупного уровня цен, не учитывающие индивидуальные свойства микрорынков [12]. Кроме того, заметим следующее. Дело в том, что в реальности не существует совокупного уровня цен, чем и объясняется абстрактный характер всех агрегатных построений. Тем не менее макроэкономическая теория имеет дело именно с агрегированными показателями. В этой связи выявление свойств последних служит для своеобразного укрепления теоретического «каркаса» макроэкономических построений, чем и определяется значимость данной проблемы.
Рассмотренные теоретические модели динамики цен основаны на гипотезе зависимости изменения цены от соотношения спроса и предложения. Основной и, на наш взгляд, достаточно продуктивный методический прием анализа таких моделей заключался в параметризации коэффициентов чувствительности спроса и предложения по ценам, т. е. предполагалась их стабильность во времени. Это позволяет более тонко изучить динамические эффекты в формировании цен на различные группы товаров (прежде всего для обыкновенных товаров и для товаров Гиффина). Для этих целей в зависимости от комбинаций параметров эластичностей спроса и предложения по ценам дана более полная классификация товаров по типам, что имеет существенное значение при рассмотрении ценовых эффектов в динамике. Из рассмотренного множества моделей ценообразования, по-видимому, наиболее предпочтительной следует признать модель (7).
Используемое предположение о постоянстве эластичностей спроса и предложения по ценам существенно огрубляет реальные процессы. В этой связи такие модели эффективно описывают ценовые эффекты на коротких интервалах времени. Понятно, что при изменении конфигурации параметров модели автоматически модифицируется вид траектории цен. Таким образом, динамический процесс ценообразования может быть представлен кривой, отдельные «куски» которой соответствуют определенному набору параметров эластичности. Однако используемый подход не позволяет выяснить особенности переходных процессов, которые характеризуются переключением параметров с одной величины на другую. Некоторые свойства таких процессов могут быть изучены путем проведения численных экспериментов.
Представленные модельные схемы, характеризующие функционирование товарных микрорынков, могут быть также использованы и для описания макропроцессов. В частности, можно исследовать динамику заработной платы на рынке труда. Рассмотренный способ агрегирования траекторий микроцен позволяет «нащупать» направления макро–микросинтеза.
[1] Данный аспект проблемы подробно анализируется в работе: Балацкий Е.В. О дискретном характере процесса ценообразования//Вестн. Моск. ун-та. Сер. Экономика. 1994. № 5.
[2] См.: Интрилигатор М. Математические методы оптимизации и экономическая теория. М., 1975.
[3] См.: Казанцев С.В. Теоретические модели цен (критический анализ буржуазных концепций). Новосибирск, 1987.
[4] См.: Антонов М.В., Трофимов Г.Ю. Аномальные эффекты торговли инсайдеров//Экономика и мат. методы. 1994. Т. 30. Вып. 2.
[5]См.: Казанцев С.В. Указ. соч.
[6] Klein L.R., Preston R.S. Stochastic nonlinear models//Econometrica. 1969. Vol. 37, No. 1.
[7] См.: Журавлев С.Н. Переход к свободным ценам: возникнет ли безработица?//Экономика и мат. методы. 1991. Т. 27. Вып. 5.
[8] См.: Белых А.А. В.А.Базаров как экономист–математик//Экономика и мат. методы. 1989. Т.25. Вып.6.
[9] См.: Поманский А.Б., Трофимов Г.Ю. Математические модели в теориях экономического цикла//Экономика и мат. методы. 1989. Т. 25. Вып. 5.
[10] См.: Карташев А.П., Рождественский Б.Л. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. М., 1986.
[11] См.: Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. М., 1986.
[12] См.: Вейцман М.Л. Простая макроэкономическая теория участия в прибылях//Экономика и мат. методы. 1989. Т.25. Вып.6.
Официальная ссылка на статью:
Балацкий Е.В. Осциллирующие траектории в моделях динамики цен// «Вестник Московского университета. Серия 6, Экономика», №1, 1995. С.26–39.