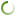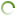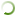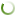Одна из основных экономических проблем современности – безработица. Методы косвенного государственного регулирования предполагают решение данной проблемы путем стимулирования деловой активности и, соответственно, уровня занятости. Со времен Дж. М. Кейнса ключевая роль в использовании макроэкономических рычагов отводится механизму мультипликатора. На сегодняшний день экономической теории известно множество разнообразных мультипликативных эффектов, которые пронизывают отдельные сферы экономики. Однако комплексная теория регулирования занятости с точки зрения действия экономических мультипликаторов пока отсутствует. Нет и унифицированной системы самих экономических мультипликаторов, позволяющей проследить взаимосвязи между отдельными мультипликативными механизмами. В свою очередь, отсутствие адекватного теоретико–методического инструментария не позволяет хотя бы приблизительно оценить возможности государства при решении проблемы безработицы.
Рассмотрим весь экономический кругооборот, начинающийся с государственных макровоздействий и завершающийся приростом численности занятых. Подобный анализ базируется на отслеживании цепочки мультипликаторов, задействованных в указанном кругообороте. При этом все рассматриваемые мультипликаторы будут построены в максимально общем и вместе с тем предельно простом виде. Следует отметить, что мы не будем учитывать отдельные частные случаи мультипликативных зависимостей, которые присутствуют в многочисленных современных теоретических моделях, сфокусируем все внимание на анализе только "классических" макроэкономических мультипликаторов. Основная же цель работы – в системном изложении мультипликативной теории макроэкономического регулирования занятости и возможностей ее применения в современных условиях.
Денежно-кредитное регулирование занятости
Говоря о денежно–кредитной политике в отношении занятости необходимо четко представлять все звенья данного регулятивного процесса. Рассмотрим их более подробно.
Прежде всего о сущности денежно–кредитной политики, под которой понимается возможность государства управлять объемом предложения денежной массы. Однако в реальности такое управление напрямую невозможно и осуществляется косвенным образом посредством эмиссионного механизма. Конкретно данная акция реализуется в виде эмиссии или детезаврации Центральным банком страны так называемых центральных денег R, которые представляют наличные платежи денежно–кредитной системы [1][1]. Технически выпуск или ликвидация центральных денег осуществляется государством путем проведения Центральным банком операций на открытом рынке по купле = продаже ценных бумаг; возможна и прямая денежная эмиссия банкнот (или их уничтожение). Мероприятия по увеличению R одновременно подкрепляются политикой ликвидных средств, заключающейся в строгой регламентации нормы резервирования п: доля n средств коммерческих банков, хранимых в Центральном банке в виде центральных (наличных) денег, строго определена. В этом случае денежная масса М складывается из обязательных резервов R и банковских денег (кредитов) К, то есть безналичных платежей: М=К+R. Выпуск коммерческими банками "бухгалтерских" (расчетных) денег К лимитирован коэффициентом ликвидности n: К=(1–n)М [1]. Тогда прирост всей денежной массы ∆M в результате эмиссии центральных денег ∆R составит: ∆М =A∆R, где А=1/n – кредитный мультипликатор (иногда А фигурирует в теории под названиями банковского мультипликатора, мультипликатора текущих счетов [2], мультипликатора создания денег [3]).
Так как банковская система реагирует на рост ∆R увеличением кредитов в соответствии с коэффициентом обязательных резервов n, то это позволяет государству, задействуя эффект кредитного мультипликатора, повышать денежно–кредитную активность экономической системы в необходимых ему размерах. Разумеется, монетарная политика государства не ограничивается регулированием денежных резервов R. Последняя предполагает также активную политику процентных ставок, введение лимитов кредитования, предоставление льгот по кредитам, выделение целевых кредитов, поддержание определенного соотношения между краткосрочными и долгосрочными кредитами, законодательные изменения и корректировки кредитного механизма и т.п. Однако удовлетворительно формализовать воздействие большинства таких мер на уровень деловой активности, как правило, не удается. В данной работе ограничимся рассмотрением макроэкономических последствий вариации переменных R и n.
Согласно Ж. Денизе, точка зрения которого отражает современные представления о хозяйственном механизме [3], именно инъекция денежной массы ∆M определяет объемы производства и инвестиций. Формально данная связь имеет вид: М–Z=kY, где Z – объем денежных средств, тезаврируемых экономическими агентами; Y – объем производства (доход или выпуск) в стоимостном выражении (валовой внутренний продукт); k – коэффициент А. Маршалла, который представляет собой долю номинального дохода экономических субъектов, хранимого в виде номинальных денежных остатков; в некоторых случаях вместо k удобно использовать показатель скорости обращения денег V=1/k [4][2]. Методологическая основа проводимых построений – учет возможного изъятия из оборота определенной части денежных средств путем их временного "связывания". Как правило, факт тезаврации отражает намерения экономических субъектов в отношении будущих вложений своих средств. По сути дела, введение в анализ феномена тезаврации означает учет спекулятивного спроса на деньги [4]. Последний в соответствии с кейнсианской теорией в общем случае зависит от процента, отражая тем самым проблему выбора экономическим агентом сферы вложения наличных денег: депонирование в банке или купля ценных бумаг. Мотив предосторожности Кейнса, связанный с резервированием наличности на непредвиденные цели, распределяется между трансакционным и спекулятивным спросом [4].
Если предположить, что объем тезаврации составляет фиксированную долю β от сбережений S домашних хозяйств, то Z=βS=β(Y–С0), где С0 – объем потребления в стоимостном выражении. Введя понятие предельной склонности к потреблению с=dC0/dY, равной удельному весу потребления в общей массе дохода с=C0/Y, и учитывая налоговые платежи, получим: Z=βY [1–с(1–θ)], где θ – налоговая ставка. Параметр θ в рассматриваемом случае позволяет учесть влияние налоговой системы на масштабы потребления и сбережений путем вычитания из дохода Y соответствующих налоговых рестрикций θY: С0=(1–θ)сY. Величина kY в данном контексте представляет собой трансакционный спрос на деньги, то есть операционный спрос на деньги для проведения экономических операций по обслуживанию товарных потоков. Используя положение о постоянстве в краткосрочном периоде общей структуры хозяйственных сделок k, легко получить выражение: ∆Y=В∆М, где В=1[k+β(1–с(1–θ))] – денежный мультипликатор. Без учета действия налоговой системы (θ=0) мультипликатор В превращается в денежный мультипликатор Л. Столерю [3].
Следует отметить, что при выведении формулы денежного мультипликатора В косвенно предполагалось ограничение Z<R, то есть объем тезаврируемых средств не может превышать величины наличных денег, циркулирующих в экономической системе. Чтобы учесть данное ограничение, предположим, что тезаврируется доля α всей суммы центральных денег: Z=αR. Тогда формула для денежного мультипликатора будет иметь вид: В–V(1–αn). Последняя отличается от формулы, выведенной ранее, составом переменных и их конфигурацией. В дальнейшем обе формы денежного мультипликатора можно использовать как равноправные.
Использование понятий кредитного и денежного мультипликаторов позволяет получить простую зависимость между ростом производства и денежно–кредитной политикой государства: ∆Y=AB∆R. В системе макроэкономических расчетов получение значения ∆Y часто является самодостаточным и дальнейшее построение цепочки мультипликативных связей можно прекратить. Уже на данном этапе можно приблизительно оценить возможный прирост занятости, исходя из того, что Y =πN, где N – численность всех занятых в народном хозяйстве; π – средняя производительность труда. Тогда ∆Y=π∆N+N∆π. Используя показатель темпа прироста производительности труда υ=∆π/π, получим соотношение
∆N = –υ N + (АВ/π)∆R (1)
Формула (1) позволяет оценить воздействие денежно–кредитных рычагов на рост занятости исходя из предполагаемого роста производительности труда. Однако показатель производительности в реальности, как правило, оказывается слабопредсказуемым. Это обусловлено многими причинами, в том числе связью производительности с тенденциями научно–технического прогресса, которые имеют чрезвычайно неустойчивый характер. В этой связи, чтобы выразить ∆N через более стабильные институциональные параметры, продолжим рассмотрение мультипликативных эффектов. Для этого необходимо пойти в обратном направлении, анализируя процесс распределения валового внутреннего продукта (см. рис.). В данном случае нас будет интересовать связь объема производства с величиной инвестиций I. В самом общем виде указанная связь может быть отображена следующим макроэкономическим балансом [3]: (Y–С0)+(J–E)=I+G, где J – импорт страны (во внутренних ценах); Е – объем экспорта (во внутренних ценах); G – государственные расходы. Так как Со=сY(1–θ), то записанное соотношение по сути дела выступает как уравнение экономического равновесия, одновременно учитывающее государственные доходы и расходы и внешнеторговые операции.
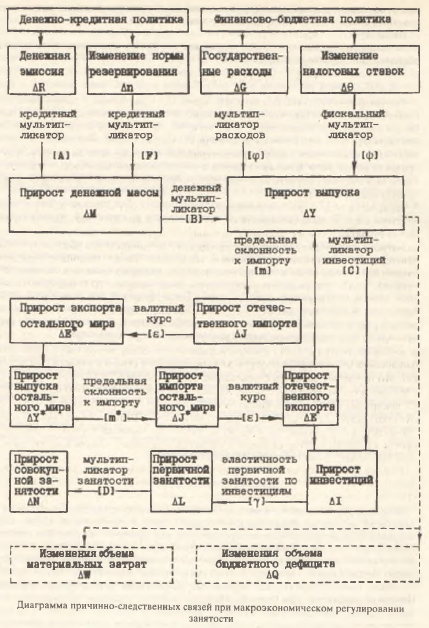
Вводя понятие предельной склонности к импорту т=dJ/dY (то есть т представляет долю импорта в валовом внутреннем продукте т=J/Y) с учетом сказанного уравнение общего равновесия перепишется в виде:
[1 + m – c (1 – θ)] Y – E = I + G (2)
Соотношение (2) является ключевым при анализе связи между приростами дохода и инвестиций. Учитывая, что G фиксировано, изменение Y в общем случае вызывает сдвиги не только в объеме инвестиций, но и экспорта. Исходя из того, что потолком для экспорта E служит спрос на экспортируемую продукцию со стороны "остального мира" [5], с которым торгует рассматриваемая страна, итоговую формулу для прироста инвестиций ∆I можно вывести с учетом реакции зарубежных доходов. Для этого необходимо получить значение ∆Е, для чего проследим следующую экономическую цепочку (см. рис.).
Прирост дохода в рассматриваемой стране вызывает прирост импорта в соответствии с предельной склонностью к импортированию: ∆J = m∆Y. Данная величина импорта равна объему экспорта остального мира: ∆Е* = ɛ∆J, где ɛ – величина валютного курса между денежными единицами торгующих стран (звездочкой обозначаются соответствующие переменные остального мира). Подобное расширение внешней торговли ведет к увеличению дохода остального мира на величину ∆Е*, то есть ∆Y* = ∆Е*. В свою очередь, полученный прирост ∆Y* распределяется в соответствии с устоявшейся структурой расходов и, в частности, определенная его часть идет на увеличение импорта с учетом предельной склонности к импортированию, сложившейся в остальном мире: ∆J* = m*∆Y*. Так как импорт ∆J* является экспортом для рассматриваемой нами страны, то ∆Е=(1/ɛ)∆J*=mm*∆Y. Таким образом, благодаря отклику доходов внешнеторговых партнеров часть национальной финансовой утечки в виде импорта ∆J возвращается в страну в качестве экспорта ∆E. Все это позволяет записать соотношение: ∆Y = С'∆I, где С'=1/[1+т(1–т*)–с(1–θ)] – мультипликатор инвестиций. Характерно, что при т* = 0, θ = 0 мультипликатор С' превращается в мультипликатор внешней торговли [5] (иногда его называют мультипликатором расходов в открытой экономике). Если же пренебречь и внешнеэкономическими связями (т=0), мультипликатор внешней торговли трансформируется в мультипликатор расходов в закрытой экономике, то есть в не что иное, как мультипликатор инвестиций Дж. М. Кейнса [6].
Строго говоря, выведенная формула для мультипликатора инвестиций предполагает, что вся импортируемая продукция идет на потребление. Однако в большинстве случаев это не так. Многие страны ввозят высокотехнологичную инвестиционную продукцию в виде производственного оборудования и ноу-хау. Это означает, что общий объем инвестиций должен учитывать и величину инвестиционного продукта иностранного происхождения, долю которого в составе импорта обозначим через η=J0/J, где J0 – стоимость импортной продукции инвестиционного назначения. Тогда суммарный объем капиталовложений складывается из внутренних и внешних инвестиций: ∆I=(1/С')∆Y+mη∆Y. Итоговое соотношение примет вид: ∆Y =С∆I, где С=1/[1–с(1–θ)+т(1–т*+η))] – обобщенный мультипликатор инвестиций. Несложно видеть, что при η → 0 С → С'[3].
Построенный мультипликатор инвестиций позволяет увязать прирост инвестиционных средств с денежно–кредитными мероприятиями правительства по стимулированию деловой активности: ∆I=(AB/C)∆R. Следующее звено экономического кругооборота связано с возрастанием первичной занятости L, порождаемым инвестиционной порцией ∆I (см. рис.). Данное аналитическое звено является совершенно естественным, так как прирост инвестиций оказывает непосредственное воздействие лишь на численность занятых в инвестиционных отраслях L. Следуя методологии Дж. М. Кейнса [6], связь между ∆I и ∆L можно отразить с помощью коэффициента эластичности первичной занятости по инвестициям γ = (I/L) (∂L/∂I). Тогда искомое выражение принимает вид: ∆L = (γL/I)∆I. В данном соотношении конструкция ∂L/∂I= γL/I выступает в качестве своеобразного инвестиционно–кадрового мультипликатора.
Последним шагом в нашем анализе является учет связи между приростом численности занятых во всей экономике ∆N и в инвестиционной сфере ∆L (см. рис.). Учитывая, что N=L+L0, где L0 – численность занятых в потребительском секторе, можно ввести коэффициент r=L0/N, характеризующий долю занятых в неинвестиционных отраслях. По аналогии с предыдущими случаями показатель r можно рассматривать как предельную склонность к расширению потребительского сектора экономики: r=dL0/dN. В результате имеем: ∆N=D∆L, где D=1/(1 – r) – мультипликатор занятости Р. Кана [6].
Общим итогом цепочки мультипликативных связей является соотношение ∆N=(γABDL/CI)∆R. Базируясь на понятиях кредитного и денежного мультипликаторов, а также мультипликаторов инвестиций и занятости, оно показывает зависимость между денежной политикой государства и ростом занятости в стране. Развернутая форма данного соотношения:
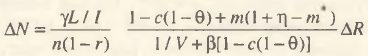 (3)
(3)
Рассмотрим полученный результат (3) и сравним его с альтернативным подходом (2).
Во–первых, во всей цепочке причинно–следственных связей ∆R → ∆N "узким местом" является кадрово–инвестиционный мультипликатор. Это связано с тем, что если показатели п, т, т*, с, r, V, β и θ представляют структурные параметры, то γ по сути своей является характеристикой динамической. Безусловно, структурные параметры тоже подвержены определенным флуктуациям даже в абсолютно стабильной среде. Однако эластичность первичной занятости по инвестициям в любом случае оказывается более подвижной. Вместе с тем в практике краткосрочных прогнозов (1 год) данный факт не составляет слишком уж существенного осложнения для процедуры макроэкономических расчетов. В этом смысле использование ретроспективных значений эластичности γ дает все же более точные результаты, нежели показатель возможного изменения производительности труда в формуле (1). Действительно, γ характеризует внутреннюю воспроизводственную структуру инвестиционной сферы, в то время как π отражает конечные результаты деятельности всего экономического организма и является менее предсказуемой. Производственная структура издержек всегда неизмеримо более инерционна, чем все ее выходные характеристики. Примечательно, что именно на стадии анализа "инвестиции – занятость" в цепочку детерминированных мультипликаторов вклинивается производственный эффект, который в формальном и содержательном плане уже достаточно жестко связан с аппаратом производственных функций, хотя непосредственно к нему и не сводится.
Во-вторых, все мультипликаторы в (3) кроме кадрово–инвестиционного представляют заведомо положительные величины. Относительно же знака эластичности γ в общем случае ничего нельзя утверждать наверняка. В обычных условиях приток инвестиций в отрасль ведет к расширению ее материально–технической базы, что сопровождается ростом численности занятых (γ > 0). Однако можно легко представить случай, когда инвестиционные вливания вызывают обновление основного капитала на трудосберегающие прогрессивные технологии (γ < 0). Данный пример — принципиален. Дело в том, что при неизменной структуре экономики, в абсолютно "спокойной" экономической среде, когда все предельные преференции экономических субъектов остаются постоянными, при γ < 0 экспансионистская денежно–кредитная политика государства может оказывать разрушительное действие на занятость. В этом случае вся цепочка макроэкономических мультипликаторов срабатывает таким образом, что только усиливает негативное действие эмиссионных мероприятий. Из сказанного вытекает, что фактором, способным опрокинуть стимулирующие монетарные действия государства, является трудосберегающий научно-технический прогресс.
Формула (1) также позволяет с несколько другой стороны рассмотреть роль технологических инноваций. В соответствии с ней прирост или сокращение занятости зависят от того, какое из воздействий оказывается сильнее: государственное стимулирование деловой активности или рост производительности труда. Если вторая группа факторов перевешивает, то все попытки стимулировать уровень занятости будут нейтрализованы. Таким образом, интенсивный научно-технический прогресс может приводить к такому вытеснению рабочей силы, что снова задействовать ее в производстве (разумеется, в течение текущего года) будет уже невозможно. Все это ведет к образованию так называемой технологической безработицы. При этом эффект мультипликатора и эффект научно–технического прогресса, выраженный через показатель производительности труда, оказываются разнонаправленными, а связь между ними не столь однозначной и категоричной, как в (3). Так, например, в благоприятных условиях государственные меры перекрывают "сдавливающее" воздействие роста производительности труда, что в итоге приводит к росту занятости. В (2) эффект научно–технического прогресса через эластичность γ органично вплетается в общую систему мультипликаторов, вызывая однозначное усиление позитивных (γ>0) или негативных (γ<0) импульсов, идущих со стороны системы государственного регулирования. Следовательно, социальные приоритеты государства требуют жестких денежно-кредитных рестрикций (∆R<0) для "борьбы" со слишком активным капиталоемким техническим прогрессом. Если же тенденция к трудосбережению в инвестиционном секторе становится устойчивой, то и кредитные рестрикции должны принимать системный характер.
Кратко рассмотрим другой вариант монетарного регулирования, связанный с изменением не величины самих резервов ∆R, а лишь нормы резервирования ∆n. Централизованное уменьшение доли наличных средств эквивалентно росту денежной массы, которая, в свою очередь, вызывает соответствующие макроэкономические возмущения, влияющие на уровень деловой активности в стране. Различие будет наблюдаться только на первой стадии цепочки экономических связей. В этом случае ∆М=FR∆n, где F=–1/n2 – модифицированный банковский мультипликатор. Несложно видеть, что F=–А/n. Тогда ∆Y=–(ABR/n)∆n. Прирост занятости может быть представлен в виде выражения, аналогичного (1). Это позволяет оценить масштабы происходящих сдвигов в численности безработных U
∆U = (ABR/πn)∆n+[h+υ(1 – ω)]H (4)
где Н – предложение рабочей силы, U=Н–N; h – темп прироста рабочей силы, h = ∆Н/Н; ω – уровень безработицы, ω = U/Н = 1 – N/H. Величина прироста предложения труда ∆Н в выражении (4) является квазиэкзогенной, так как она по сути дела аккумулирует в себе группу как экзогенных (временная структура рождаемости и смертности населения), так и эндогенных (уровень трудовой активности трудоспособного населения) факторов. Таким образом, изменение численности безработных зависит от трех народнохозяйственных аспектов: научно–технического прогресса; социально–демографических характеристик; чисто экономического фактора, связанного с регулятивной функцией государства. При этом из (4) хорошо видна принципиальная ограниченность государственного вмешательства. Роль последнего при воздействии на масштабы безработицы оценивается первым компонентом в правой части (4); второй компонент фиксирует влияние автономных экономических сдвигов, которые зависят от тенденций, сложившихся в предшествующие периоды времени, и не подлежат непосредственной целенаправленной оперативной корректировке под нажимом государства.
Аналогично формуле (3) прирост занятости при изменении нормы резервирования в развернутом виде с учетом всех мультипликативных зависимостей может быть представлен следующим образом
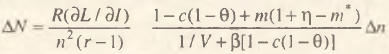 (5)
(5)
Если Центральный банк оперирует обоими рычагами ∆R и ∆n одновременно (например, уменьшая норму резервирования и увеличивая объем наличности), то суммарный прирост занятости оценивается путем сложения (3) и (5). Здесь уместно отметить ограниченность варьирования ∆n и ∆R. Особенно это касается нормы резервирования; в подавляющем большинстве случаев диапазон ∆R значительно шире. В этом смысле сочетание обоих денежно–кредитных регуляторов n и R позволяет снизить нагрузку, приходящуюся на каждый из них при монетарном монорегулировании.
В заключение рассмотрим два условных примера, показывающих возможное практическое применение формул (3) и (5).
ПРИМЕР 1. Пусть предельная склонность к импортированию в анализируемой стране равна 20%, а в остальном мире – 10%; предельная склонность к потреблению внутреннего продукта – 60%; средняя норма налоговых изъятий – 25%; скорость обращения денег – 0,5 оборот/год; предельная склонность к тезаврации – 15%; норма резервирования – 20%; доля занятых в потребительском секторе – 50%; эластичность занятости в инвестиционном секторе по объему инвестиций – 0,3; объем инвестиций в первоначальный момент времени – 60 млрд. долл. (для определенности в качестве денежной единицы будем использовать доллар); численность занятых в инвестиционной сфере в начальный момент времени – 35 млн. человек; объем наличности в экономике в начальный момент времени – 120 млрд. долл.; инвестиционный продукт в составе импорта отсутствует.
Необходимо определить, насколько изменится численность занятых при денежной эмиссии в 10 млрд. долл.
Используя формулу (3), получим, что для заданной структуры экономики и начальных значений макропеременных денежно–кредитный мультипликатор занятости, связывающий ∆N и ∆R, равен 0,61. Отсюда автоматически вытекает, что прирост наличности (эмиссия) на 10 млрд. долл. ведет к увеличению численности занятых в экономике на 6,1 млн. человек.
ПРИМЕР 2. Для исходных параметров экономики, заданных в примере 1, необходимо определить изменение уровня занятости, вызванное уменьшением нормы резервирования на 2%.
Использование формулы (5) показывает, что величина модифицированного денежно–кредитного мультипликатора, связывающего ∆N и ∆n, равна 366. Это означает, что 2%–ное послабление в отношении нормы резервирования равносильно увеличению численности занятых на 7,3 млн. человек.
Финансово-бюджетное регулирование занятости
Рассмотрим теперь воздействие финансово–бюджетной политики государства на масштабы занятости. К числу рычагов финансово–бюджетной политики относятся государственные расходы и налоговые ставки. Манипулируя данными величинами, государство может влиять на уровень деловой активности в стране, тем самым формируя необходимую экономическую среду для расширения занятости (см. рис.).
С методологической точки зрения финансово–бюджетное регулирование в отличие от кредитно–денежной политики достигает поставленной цели более "коротким" путем, напрямую воздействуя на совокупный выпуск ∆Y. Это связано с тем, что экзогенные сдвиги в государственных расходах и налоговых ставках представляют собой не косвенное, а непосредственное регулирование денежной массы в обращении. Так, например, рост государственных расходов может покрываться либо за счет денежной эмиссии, либо за счет роста государственного долга в результате осуществления внутренних или внешних государственных займов. Монетарный характер фискальных изъятий очевиден.
Проанализируем более подробно связь между уровнем выпуска и объемами государственных расходов. Для этого воспользуемся подходом П.Х. Линдерта [5]. Упрощенные выкладки по усеченной схеме внешнеторговой цепочки показывают, что в этом случае ∆Y = φ∆G, где φ – мультипликатор государственных расходов: φ = 1/[1 + т (1 – т*) – с (1 – θ)]. Несложно видеть, что мультипликатор государственных расходов φ совпадает с выведенным ранее мультипликатором инвестиций при η = 0. Данное утверждение является истинным как для полной схемы международного сотрудничества, учитывающей весь мультипликативный цикл (в этом случае φ̴̃= С̃, где η = 0), так и для ее усеченного варианта. Дальнейшая цепочка экономических связей аналогична той, что действует при монетарном регулировании (см. рис.). Однако в этом случае при η = 0 получаем ∆I = ∆G, то есть вся величина государственных расходов направляется на внутреннее инвестирование. Это не совсем верно и получается из-за того, что нами дважды учитывается эффект возрастания экспорта – за счет ∆G и за счет ∆Y. Чтобы нейтрализовать погрешности, возникающие в результате двойного счета внешнеторговых эффектов, мультипликатор инвестиций в данной схеме должен вычисляться без учета реакции зарубежных партнеров, то есть при т* = 0. Инвестиционно-кадровый мультипликатор и мультипликатор занятости Р. Кана при бюджетном регулировании не изменяются и общий прирост занятости в результате прироста государственных расходов в условиях постоянного фискального давления составит
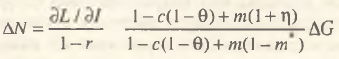 (6)
(6)
Если государство манипулирует налоговыми ставками, то в этом случае зависимость между выпуском ∆Y и изменением величины налогов ∆θ будет выражаться в виде: ∆Y = ѱY∆θ, где ѱ – фискальный мультипликатор: ѱ = –с/[1 – с (1 – θ) + т (1 – m*)] [4]. В дальнейшей цепочке мультипликатор инвестиций, как и в случае государственных расходов, берется для т* = 0, а мультипликатор занятости и инвестиционно–кадровый мультипликатор остаются прежними. Тогда общий прирост занятости, вызванный изменением налоговых ставок, равен
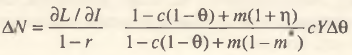 (7)
(7)
Отметим, что отличие проведенных фискальных построений от традиционных [2], [3] заключается в том, что мы рассматриваем изменение ставки самого налога, а не величины налоговых поступлений. Последний подход предполагает так называемый паушальный (аккордный) налог [2], который дает одну и ту же величину налоговых поступлений при любой величине валового внутреннего продукта и не позволяет рассмотреть роль конкретного макроэкономического рычага, используемого государством при проведении политики занятости. Кроме того, паушальный налог соответствует регрессивной налоговой системе, в то время как для большинства промышленно развитых стран типичны прогрессивные или пропорциональные (как в нашем случае) системы налогообложения.
Проиллюстрируем выведенные формулы на условных примерах.
ПРИМЕР 3. Для экономики с объемом валового внутреннего продукта 150 млрд. долл. и параметрами, заданными в примере 1, необходимо определить прирост численности занятых, вызванный ростом государственных расходов на 15 млрд. долл.
Используя формулу (6), получим величину интегрального мультипликатора, связывающего ∆N и ∆G, равную 0,36. Это означает, что при росте государственных расходов на 15 млрд. долл. занятость увеличивается на 5,4 млн. человек.
ПРИМЕР 4. Для экономики, имеющей параметры, заданные в примере 3, необходимо определить прирост численности занятых, вызванный уменьшением налоговых ставок в среднем на 2%.
Расчеты по формуле (7) показывают, что 2%–ные налоговые скидки в заданных условиях могут привести к росту масштабов занятости на 6,5 млн. человек.
Подчеркнем, что выведенные в данной работе формулы (3), (5), (6) и (7) дают оценку автономных, независимых друг от друга, действий государства. В реальности проблема безработицы практически никогда не решается за счет какого-либо одного макроэкономического рычага. Одновременное использование средств, имеющихся в распоряжении государства, позволяет, во-первых, достичь более ощутимых результатов за счет их совместного действия, а, во-вторых, так скомбинировать все виды мероприятий, чтобы не допустить чрезмерной нагрузки на какие-либо из них. Последний момент чрезвычайно важен, так как диапазон возможных эффективных изменений ∆R, ∆n, ∆G и ∆θ весьма ограничен. Выход данных переменных за полосу допустимых значений ведет либо к негативным побочным последствиям, которые делают экономическую систему слабоуправляемой, либо к тому, что на дальнейшие изменения регулируемых переменных система прекращает реагировать адекватным (запланированным) образом. В этой связи в прогнозных расчетах целесообразно использовать формулы (3), (5)–(7) совместно, для чего необходимо просто сложить их правые и левые части. В этом случае общий прирост занятости будет зависеть от четырех различных государственных мероприятий, каждое из которых может играть лидирующую роль в зависимости от экономической ситуации. Подобная схема позволяет проводить вариантные расчеты при разработке мер государственного регулирования занятости. Благодаря имеющемуся эффекту взаимозаменяемости рассматриваемых макроэкономических рычагов возможны их синхронизация и координация, исходя из априорно заданных целей и социальных приоритетов.
Более подробное рассмотрение фискальных эффектов связано с изучением влияния агрегированного налога на инвестиции и экспортно–импортных тарифов. Методология анализа остается прежней: в исходном уравнении (2) показатели т, Е и I будут домножаться на соответствующие налоговые ставки. Совместное рассмотрение уравнения (2) для "нашей" страны и для остального мира позволяет получить формулы мультипликаторов для налоговых ставок и таможенных тарифов. Во многих случаях варьирование ставками таможенных пошлин оказывает заметное влияние на уровень деловой активности в стране. Кроме того, аккумулируемые государством денежные средства от внешней торговли могут быть вторично использованы для стимулирования занятости путем расширения государственных расходов.
Включение в аналитическую схему монетарных эффектов, связанных с международной открытостью экономики, также возможно и достигается благодаря использованию так называемого депозитного (евродепозитного) мультипликатора [7], [8]. Однако в связи с наличием множества спорных вопросов в этой области детальное рассмотрение таких эффектов в данной работе проводить не будем.
Эффекты, сопутствующие государственной политике занятости
Выше рассматривались последствия государственных мероприятий для масштабов занятости и безработицы. Однако совершенно очевидно, что возможно возникновение важных побочных эффектов в результате задействования макрорычагов. В частности, один из аспектов государственного регулирования – проблема сбалансированности бюджета. В свете данной проблемы все государственные воздействия должны анализироваться с точки зрения их влияния на бюджетный дефицит Q. Учитывая, что ∆Q = ∆G – ∆Т, где Т – налоговые поступления в бюджет (Т=θY), выведенные формулы для макроэкономических мультипликаторов позволяют достаточно просто оценить изменения в сумме налоговых платежей, а, следовательно, и сдвиги в бюджетном дефиците. Для примера запишем формулу для прироста налоговых поступлений, вызванных изменением величины налоговой ставки. Так как ∆Т=θ∆Y+Y∆θ, то имеем зависимость ∆Т=(1+θѱ)Y∆θ. Тогда формула для сдвигов в масштабах бюджетного дефицита при осуществлении государственных расходов AG и изменении налогов ∆θ выглядит следующим образом [5]:
∆Q = ∆G – [(1 + ѱθ) Y∆θ + φθ∆G] (8)
В квадратных скобках здесь обозначена величина налоговых поступлений ∆Т, которая учитывает возврат части государственных расходов в результате их трансформации в доходы налоговой системы. Аналогичным образом могут быть получены соотношения, связывающие ∆Q с ∆R и ∆n. При выборе государственной политики занятости все макроэкономические воздействия должны быть скоординированы таким образом, чтобы рост бюджетного дефицита был по возможности минимальным.
Полученная формула (8) позволяет сделать ряд дополнительных выводов и уточнений относительно способов бюджетного регулирования. Прежде всего это касается концепции так называемого мультипликатора сбалансированного бюджета [2], который показывает увеличение валового внутреннего продукта в результате одновременного увеличения государственных расходов и доходов; причем сдвиги в расходах и доходах государства одинаковы по величине и, следовательно, масштабы бюджетного дефицита при этом не изменяются. Если в начальный момент времени бюджет был сбалансирован, то подобное регулирование позволяет стимулировать рост производства при сохраняющемся бюджетном равновесии (указанный факт и определил название данного мультипликатора). По-видимому, излишне доказывать важность такого "аккуратного" способа финансово–бюджетного регулирования.
Вывод мультипликатора сбалансированного бюджета достаточно очевиден. Для этого необходимо выразить ∆θ из уравнения (8) через ∆G с учетом того, что ∆Q = 0. Учитывая, что в данном случае задействованы два экономических рычага ∆θ и ∆G, то совокупный прирост дохода ∆Y будет складываться из двух величин: ∆Y = φ∆G + ѱY∆θ. Тогда получим формулу ∆Y = λ∆G, где λ=(1–с)/[1–с+т(1–т*)] – мультипликатор сбалансированного бюджета и ∆G=∆Т. Легко видеть, что без учета внешнеэкономических эффектов (т=0) данный мультипликатор равен единице, как это и утверждается в [2] [6]. Если в регулирование занятости "вмешиваются" монетарные рычаги ∆R и ∆n, то полученная формула естественным образом обобщается. В некоторых случаях точкой отсчета при разработке доходно–расходной государственной политики служит уровень бюджетного дефицита (как правило, относительно валового национального продукта), на который желательно выйти в очередном финансовом году. Формула (8) позволяет провести соответствующие расчеты с учетом элементарных корректировок.
Другим важным результатом стимулирующей государственной политики является рост материальных затрат. Причем приросты затрат и валового внутреннего продукта связаны между собой мультипликативной зависимостью. Учитывая ограниченность, а иногда и острый дефицит многих природных ресурсов, а также истощение действующих сырьевых баз, изношенность и дороговизну связанных с ними иммобильных фондов, оценка роста материальных затрат во многих случаях представляет собой особую важность.
Наибольшую разработанность в методическом отношении данный вопрос находит в схемах межотраслевого баланса. Так, например, в модели В. Леонтьева фигурирует матрица полных затрат или матричный мультипликатор [9], которому в некоторых случаях отводится роль мультипликатора затрат [10]. Однако матричная конфигурация данной конструкции не позволяет использовать ее в сводных макроэкономических расчетах. В этой связи произведем необходимую для наших целей процедуру агрегирования. Для этого "сожмем" векторное информационное поле межотраслевой модели в точку; именно точечное значение всех параметров межотраслевого баланса и позволяет перейти к макроэкономическому рассмотрению процесса.
Исходным для нас является соотношение [II]; 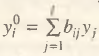 ; где
; где 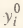 – валовой выпуск i-ой отрасли;
– валовой выпуск i-ой отрасли; 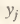 – конечный продукт j-ой отрасли; –bij – коэффициенты полных затрат i-ой и j-ой отраслей. С учетом Y0 = Y + W, где Y0 – общий объем производства;
– конечный продукт j-ой отрасли; –bij – коэффициенты полных затрат i-ой и j-ой отраслей. С учетом Y0 = Y + W, где Y0 – общий объем производства; 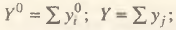 W – материальные затраты, соответствующие промежуточному (внутриотраслевому) потреблению; uj, = yJ/Y получим соотношение
W – материальные затраты, соответствующие промежуточному (внутриотраслевому) потреблению; uj, = yJ/Y получим соотношение
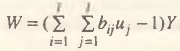 (9)
(9)
Из данной формулы автоматически вытекает зависимость ∆W = μ∆Y, где коэффициент μ равен выражению в скобках в (9) и представляет собой макроструктурный мультипликатор затрат (название обусловлено его макроэкономическим характером, учитывающим отраслевую структуру ВВП). Полученные соотношения позволяют достаточно просто рассчитать эффект увеличения материальных затрат в результате проведения тех или иных макромероприятий. Так, например, изменение денежной наличности ведет к росту материальных издержек ∆W = μAB∆R.Отметим, что помимо всего прочего мультипликатор затрат играет большую роль в ценообразовании [7]. Данный факт предопределяет особенно осторожное отношение к возможному нарастанию холостых (промежуточных) издержек производства.
Оценка побочных эффектов ∆Q и ∆W позволяет определить своего рода "бюджетоемкость" и "ресурсоемкость" всех мероприятий по стимулированию занятости. Можно предположить, что результаты подобных расчетов в ряде случаев могут оказаться настолько негативными, что будут стимулировать отказ либо от некоторых макроэкономических рычагов, либо вообще от стимулирующей политики занятости.
Применимость идеологии мультипликатора
Рассмотренная доктрина мультипликатора, несмотря на имеющиеся в ней интересные чисто теоретические аспекты, в конечном счете носит ярко выраженный прикладной характер. Мультипликаторная концепция регулирования занятости ориентирована на проведение базисных прогнозных расчетов на начальной стадии выработки макроэкономической политики. Действительно, данная концепция дает нам методический аппарат, состоящий всего лишь из нескольких простейших формул типа (3), (5) – (8) и позволяющий проигрывать различные варианты государственной политики. Результатом таких расчетов являются черновые сценарии экономических последствий действия макроэкономических регуляторов. Правда, даже самые грубые прикидки на основе теории мультипликатора возможны только при выполнении определенных условий. Для понимания этих условий проанализируем, что лежит в основе идеологии мультипликатора как таковой.
Во-первых, идеология мультипликатора базируется на принципах маржинализма, который предполагает широкое применение в экономической теории предельного анализа. Практически все современные микро– и макропостроения имеют маржиналистскую окраску, что проявляется прежде всего в активном использовании показателей эластичности, характеризующих степень гибкости тех или иных экономических переменных. В этом смысле использование в теории мультипликатора различных показателей предельных склонностей по существу представляет собой частный случай коэффициентов эластичности. Характерно, что уже Дж. М. Кейнс в полной мере использовал классические показатели эластичности наряду с показателями предельных склонностей [6]. В методическом плане указанная особенность теории мультипликатора порождает проблему вычислительных погрешностей при проведении прогнозов. Это связано с тем, что анализ бесконечно малых оперирует с непрерывными величинами, в то время как все экономические измерения носят принципиально дискретный характер. Для устранения указанного недостатка многие формулы теории мультипликатора следует переписать в конечно-разностной форме, учитывающей так называемые нераспределенные остатки.
Во-вторых, все зависимости теории мультипликатора вытекают из простых балансовых соотношений и предполагают неизменность структуры используемых балансов. Однако в реальности все структурные оценки являются неустойчивыми и флуктуируют в относительно широком диапазоне. Это означает, что соотношения типа (3), (5)–(8) должны записываться более строго (в форме частных производных), а общий прирост занятости представляет собой дифференциал и должен включать эффекты от изменения структурных параметров. Пренебрежение данным моментом может привести к серьезным погрешностям в расчетах. Трудность в решении данной проблемы заключается в случайности и непредсказуемости отклонений структурных параметров от своей нормальной (устоявшейся) величины.
В-третьих, большинство показателей (в том числе структурных) в балансовых соотношениях теории мультипликатора сложным образом связаны между собой, что порождает проблему мультиколлинеарности данных. Это проявляется в том, что изменение определенного экономического показателя в мультипликативной цепочке, воздействуя на основную выходную характеристику, оказывает систематическое воздействие и на целый ряд других характеристик. Так, например, изменение налоговых ставок способно приводить к изменению не только объемов выпуска, но и его структуры распределения. Повышательное действие на предельную склонность к потреблению и скорость обращения денег оказывают инфляционные тенденции, которые представляют оборотную сторону стимулирующей политики занятости. Учет таких эффектов требует отдельных довольно тонких исследований, результаты которых должны "навешиваться" на базовые соотношения теории мультипликатора, тем самым дополняя агрегатные расчеты.
В–четвертых, все показатели теории мультипликатора фигурируют в стоимостной форме. Денежное представление экономических переменных во внутренних ценах порождает центральную проблему всей теории мультипликатора – проблему разделения двух экономических эффектов: роста реальных (физических) объемов продукции и инфляционного роста цен. Особенно остро данный момент проявляется в отношении внешнеторговых агрегатов, включающих в себя такую подвижную характеристику, как валютный курс. Учитывая, что формальной теории передаточного механизма (способа, с помощью которого влияние денежных потоков распределяется между изменением цен и изменением реального производства [12]) не существует (и вряд ли может существовать), то указанная проблема в рамках теории мультипликатора остается по существу открытой. В этой связи отметим, что в прогнозных расчетах необходимо учитывать хотя бы ориентировочный ожидаемый темп инфляции 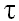 . Если Y = РХ, где X – физический объем валового внутреннего продукта; Р – средний уровень цен, то прирост номинального дохода распадается на два субэффекта: ∆Y = Х∆Р + Р∆Х. Так как для наращивания занятости имеют смысл только реальные инвестиции, исходящие из выпуска Р∆Х, то именно к величине Р∆Х в дальнейшем должна применяться вся цепочка мультипликаторов: P∆X = ∆Y –
. Если Y = РХ, где X – физический объем валового внутреннего продукта; Р – средний уровень цен, то прирост номинального дохода распадается на два субэффекта: ∆Y = Х∆Р + Р∆Х. Так как для наращивания занятости имеют смысл только реальные инвестиции, исходящие из выпуска Р∆Х, то именно к величине Р∆Х в дальнейшем должна применяться вся цепочка мультипликаторов: P∆X = ∆Y – .png) Y, где
Y, где .png) = ∆Р/Р. Тогда, например, для регулятора ∆R скорректированный прирост занятости ∆Ncкор должен рассчитываться по уточненной формуле (3)
= ∆Р/Р. Тогда, например, для регулятора ∆R скорректированный прирост занятости ∆Ncкор должен рассчитываться по уточненной формуле (3)
∆Nскоp = ∆N + δ.png) , (10)
, (10)
где δ = –γL [1 – с (1 – θ) + т (1 – m*)] [(1 – с)/(1 –.png) )]. Таким образом, оценка δ
)]. Таким образом, оценка δ.png) очищает эффект прироста занятости от искажающего влияния инфляции. Из приведенных формул видно, что стагфляция ∆Х < 0 начинается при
очищает эффект прироста занятости от искажающего влияния инфляции. Из приведенных формул видно, что стагфляция ∆Х < 0 начинается при .png) >
> .png) 0, где
0, где .png) 0 = ∆Y/Y. Чтобы эффект от государственных мероприятий не обнулился, правительство вынуждено наращивать усилия по стимулированию номинального дохода, чтобы обогнать ожидаемый темп прироста цен
0 = ∆Y/Y. Чтобы эффект от государственных мероприятий не обнулился, правительство вынуждено наращивать усилия по стимулированию номинального дохода, чтобы обогнать ожидаемый темп прироста цен .png) . Несложно видеть, что за пределами
. Несложно видеть, что за пределами .png) 0, когда процесс гиперинфляции (точнее слампфляции [12]) разворачивается в полной мере, теория мультипликатора способна только приводить либо к принципиально ошибочным выводам, либо в лучшем случае к позиции государственного невмешательства. Следовательно, формулы типа (10) работают только для определенного диапазона
0, когда процесс гиперинфляции (точнее слампфляции [12]) разворачивается в полной мере, теория мультипликатора способна только приводить либо к принципиально ошибочным выводам, либо в лучшем случае к позиции государственного невмешательства. Следовательно, формулы типа (10) работают только для определенного диапазона .png) , когда экономика является достаточно устойчивой и хорошо управляемой. Полоса устойчивости для
, когда экономика является достаточно устойчивой и хорошо управляемой. Полоса устойчивости для .png) , по-видимому, может определяться только эмпирически.
, по-видимому, может определяться только эмпирически.
В-пятых, идеология мультипликатора может быть охарактеризована как концепция "пассивного" прогнозирования. Все мультипликативные зависимости нацелены на сглаживание и усреднение экономических оценок реальных процессов. Тем самым оказываются неучтенными тенденции движения народнохозяйственной конъюнктуры, циклические особенности обновления основного капитала, сдвиги в сфере международных экономических отношений, инновационные шоки со стороны научно–технического прогресса и т.д. При этом игнорируются как текущие, так и долгосрочные (вековые) закономерности. Все названные эффекты могут улавливаться более частными моделями, результаты которых можно накладывать на мультипликаторные расчеты в качестве экзогенной информации, позволяющей более объективно оценить действенность предполагаемых мер государственного регулирования.
В-шестых, аппарат теории мультипликатора предназначен для реализации краткосрочных прогнозов на очередной финансовый год. Попытки экстраполировать результаты мультипликаторных расчетов на более продолжительный период (свыше 1 года) являются заведомо беспочвенными. Данный факт во многом предопределяет необходимость встраивания теории мультипликатора в модельный блок, включающий учет "быстрых" (краткосрочных) и "медленных" (долгосрочных) экономических сдвигов.
Таким образом, прогнозирование на базе теории мультипликатора лишь в редких случаях может применяться в автономном режиме. Как правило, подобные расчеты должны подкрепляться массой дополнительных более специфических исследований. Сказанное позволяет уяснить место мультипликаторной теории государственного регулирования занятости в общей системе макромоделей и избежать возможных ошибок при проведении конкретных прогнозных расчетов в современных условиях.
Литература
[1] Э. Р о д е. Банки, биржи, валюты современного капитализма. М. 1986.
[2] К.Р. Макконнелл, С.Л. Б р ю. Экономикс: принципы, проблемы, политика. М. 1992. Т. 1.
[3] Л. С т о л е р ю. Равновесие и экономический рост. М. 1974.
[4] Л. X а р р и с. Денежная теория. М. 1990.
[5] П.Х. Л и н д е р т. Экономика мирохозяйственных связей. М. 1992.
[6] Дж.М. Кейнс. Общая теория занятости, процента и денег. М. 1978.
[7] И.В. Филаточев. Концепции "открытой экономики": интернационализация и макроэкономическая политика государства. М. 1991.
[8] А. Р о г о в и ц к и й. Евровалюты в кредитно–денежной системе капитализма ("Мировая экономика и международные отношения", N9. 1985).
[9] В.И. Д у д о р и н, В.В. Капитоненко, О.Е. Блинов, Н.Б. Филинов–Чернышев. Основные принципы и базовые модели экономической кибернетики. М. 1982.
[10] А.Б. Виссарионов. Развитие ценового и финансово–кредитного механизмов в России. М. 1994.
[11] "Моделирование народнохозяйственных процессов". М. 1973.
[12] М. Б л а у г. Экономическая мысль в ретроспективе. М. 1994.
[13] О.Ю, Шибалкин. Анализ структуры инфляции издержек в российской экономике ("Экономика и математические методы". Том 31. Вып. 2. 1995).
[1] Здесь и далее в квадратных скобках обозначаются ссылки на литературу.
[2] Обратим внимание на то, что при Z = 0 записанное выражение представляет собой нечто иное, как уравнение И. Фишера (или кембриджское уравнение денежной теории) [4].
[3] В первом приближении выведенная формула для мультипликатора инвестиций достаточно точно отражает исследуемый процесс (с точностью до первого порядка); в общем случае представленная внешнеторговая цепочка повторяется многократно, порождая в каждом экономическом раунде постепенно затухающий мультипликативный эффект. Чтобы вывести полную формулу мультипликатора инвестиций, необходимо рассмотреть одновременно два уравнения (2): для искомой страны и для остального мира.
Принципиальная разница данного подхода заключается в том, что прирост дохода остального мира ∆Y* не будет совпадать с приростом экспорта ∆Е*. Итоговая формула в этом случае примет вид
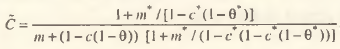
С учетом структуры импорта прирост инвестиций составит ∆I = (1/Ĉ + mη)∆Y. Несложно видеть, что данная формула учитывает структуру потребления и налоговый климат остального мира. Такая конструкция является естественным обобщением мультипликатора расходов с реакцией зарубежного дохода [5] с точки зрения налогового законодательства, действующего в странах–контрагентах. В дальнейшем вместо данного соотношения используем менее громоздкий предыдущий вариант мультипликатора инвестиций.
[4] В общем виде фискальный мультипликатор выглядит следующим образом: ѱ̃ = –сС (см. сноску 3).
[5] Более строго ∆Т = θ∆Y + Y∆θ + ∆θ∆Y. Тогда формула (8) может быть уточнена следующим образом
∆Q = (1 – φθ)∆G – (1 + ѱθ) Y∆θ – [φ∆G∆θ + ѱY (∆θ)2].
Довесок в квадратных скобках учитывает эффект обложения налогом величины прироста валового внутреннего продукта. В ряде случаев оценка данного корректирующего компонента может быть весьма значительна, представляя макроэкономическую величину, которой нельзя пренебречь.
[6] В более общем случае λ = (φ + ѱ) / (1 + ѱθ). Мультипликатор λ может быть выражен в максимально полной форме, если φ = φ̃, а ѱ = ѱ̃.
[7] В [13] показатель ζ = Y/Y0 используется для оценки степени инфлятогенности и инфляционной уязвимости народного хозяйства в целом. В наших обозначениях мультипликатор затрат μ связан с ζ очевидным соотношением: μ = 1/ζ - 1.
Официальная ссылка на статью:
Балацкий Е.В. Регулирование занятости в свете теории мультипликатора// «Мировая экономика и международные отношения», №5, 1996. С.53–67.