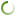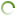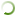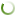По теории налогов уже накопилась довольно многочисленная отечественная литература (например, [1–4]). Большинство работ предполагает исследование налоговых эффектов, во-первых, для достаточно стабильной экономической среды, а, во-вторых, с помощью нормативных (оптимизационных) моделей. По мнению автора, наиболее содержательной является статья [4], в которой рассмотрены налог на прибыль и налог на добавленную стоимость (НДС).
В данной работе исследуем эти же 2 основных вида налогов, являющихся наиболее значимыми фискальными инструментами. Большинство "мелких" налогов по своему функциональному назначению и механизму действия идентичны налогу на прибыль или НДС и формально могут быть сведены к одному из них путем соответствующего агрегирования (проблему налогового агрегирования см., в частности, в [5]). Проанализируем действие фискальных регуляторов применительно к условиям перманентной инфляции без учета ограничивающего влияния со стороны спроса, так как его изменения под давлением роста цен, как правило, неоднозначны и требуют самостоятельного изучения. Иными словами, спрос задается экзогенно таким образом, что не сдерживает производства. Кроме того, в инструментальном плане используем дескриптивный подход к определению стратегии фирмы в конкурентной среде в отличие от традиционных оптимизационных постановок задач.
Дескриптивная модель производственных стратегий фирмы
При описании функционирования производственных объектов необходимо иметь представление о целевых установках руководства предприятия. Однако, несмотря на всю важность, данный вопрос не имеет однозначного решения в современной микроэкономике. Так, например, в простейшей классической постановке в качестве критерия оптимальности деятельности фирмы выступает показатель валовой прибыли [6]. В задаче У.Баумоля максимизируется стоимость реализованной продукции [4]. Авторами [4] использовался усложненный критерий, представляющий собой выпуклую комбинацию объема выпуска и чистой прибыли, которая остается в распоряжении предприятия после уплаты налогов. При этом весовая функция, с помощью которой происходит свертка двух субцелей фирмы, в общем случае зависит от налоговых ставок. Такой подход объединяет в себе как традиционные предпосылки экономического анализа, заключающиеся в максимизации предпринимателем объемов прибылей, так и "рыночный” аспект, связанный со стремлением производителя к монополизации рынка путем расширения объемов выпуска.
Однако в условиях постоянной и достаточно сильной инфляции такие абсолютные показатели вряд ли могут быть надежным индикатором эффективности функционирования фирмы. В таких случаях необходимо использовать относительные характеристики. В частности, в [7] автор использовал показатель нормы прибыли (рентабельности) как отношение валовой прибыли к текущим издержкам. В данной работе при построении теории фирмы целевые установки предпринимателей будут задаваться эластичностью чистой прибыли по ценам: Е=(P/π)(dπ/dP), где Р – цена продукции, выпускаемой фирмой; π=(1–α)[(1–β)(PX–CR)–WL] – чистая прибыль предприятия; α – налог на прибыль; β – налог на добавленную стоимость; X – объем производимой продукции (выпуск) в натуральном выражении; R – издержки производства в натуральных единицах (сырье, материалы, полуфабрикаты и т.п.), R=R[X(P)]; С – цена издержек, С=С(Р); W – средняя заработная плата работников фирмы, W=W(P); L – численность персонала фирмы, L=L[X(P)].
Предположим, что изменение цены Р под действием инфляции навязывается производителю извне, то есть развитие процесса происходит в конкурентной среде. В свою очередь, в соответствии с раскладом "сил" на товарных и ресурсных рынках инфляционные тенденции полностью определяют изменения в уровне оплаты труда и цен на сырье, которые характеризуются эластичностями φ=(P/W)(dW/dP) и ζ=(P/C)(dC/dP), соответственно. Изменение ресурсных издержек и численности персонала зависит от сдвигов в объеме производства в соответствии со сложившимися технологическими особенностями фирмы, определяемыми эластичностями η=(X/R)(dl/dX) и ѱ=(X/L)(dL/dX). Таким образом, в ответ на происходящие ценовые сдвиги фирма может манипулировать только объемами выпуска. Если в такой ситуации предприниматель придерживается заранее сформулированной позиции в отношении изменения реальной прибыльности предприятия (то есть Е экзогенно задана), то производственная стратегия фирмы полностью предопределена и описывается следующим дифференциальным уравнением:
E[(1–β)(PХ–CR)–WL]=(1–β)[PX+P2(dX/dP)–ζCR– ηСR(Р/Х)(dX/dP)]– ѱWL–φWL(P/X)(dX/dP).
Данное уравнение получается в результате дифференцирования π по Р. Если предположить, что все эластичности постоянны, то С = αРζ; R = bХη; W = nРφ; L = тХѱ, где α, b, n и m – постоянные интегрирования, играющие роль масштабирующих коэффициентов. С учетом данных зависимостей приведенное уравнение перепишется относительно переменных Р и Х в явном виде. Однако подобное уравнение практически неразрешимо в силу высокой степени нелинейности. Так как мы используем метод сравнительной статики и, следовательно, анализ ведется для малых интервалов (то есть имеет место "точечный” анализ), то для упрощения всех дальнейших построений будем аппроксимировать степенные функции их линейными приближениями [1]. Тогда используя обозначения
А = Е – 1 + abζη(ζ – Е) – nmφѱ(1 – φ)/(1 – β) (1)
В = abη(ζ + 1)(η – 1) – nmѱ(1 + φ)(1 – ѱ)/(1 – β) (2)
дифференциальное уравнение для производственной стратегии фирмы в инфляционной обстановке запишем в виде:
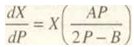 (3)
(3)
Его решением является простая экспоненциальная функция [7]:
X = μехрА[Р/2 + (В/4)ln(2P – В)], (4)
где μ – постоянная интегрирования.
Выведенное уравнение (3) представляет искомую дескриптивную модель поведения производителя в условиях роста цен на готовую продукцию, ресурсы и труд при заданных технологических ограничениях. Формула (4) задает в явном виде траекторию развития производства в зависимости от структуры инфляции на товарных и ресурсных рынках. Понятно, что для различных наборов параметров модель (4) позволяет проигрывать производственную ситуацию, чем и объясняется ее поведенческий характер. При этом активная позиция руководителя фирмы задается параметром Е. который фиксирует своего рода предпринимательскую "жадность". Простая, наглядная и аналитичная форма соотношения (4) дает возможность использовать его в дальнейшем при разборе различных экономических вопросов.
Денежная иллюзия на рынке труда
Прежде чем перейти к рассмотрению собственно налоговых эффектов коснемся чрезвычайно важного вопроса, связанного с формированием спроса и предложения на ресурсных рынках. В методологическом плане данный вопрос тесно связан с полученной дескриптивной зависимостью (4) и органично дополняет ранее начатое автором исследование о форме кривых спроса и предложения, позволяя распространить предложенный подход на ресурсные рынки.
В работе [7] автор подробно разбирает вопрос о форме кривых спроса и предложения для "готовых" товаров (то есть конечных продуктов производства). Однако подобный вопрос правомерен и для товаров–ресурсов (то есть товаров производственного назначения), который в [7] не рассматривался, так как предполагает несколько иную методологию исследования. В данной работе ограничимся анализом рынка рабочей силы, заметив, что на любой другой производственный ресурс полученные результаты распространяются автоматически с небольшими содержательными коррективами.
Основным тезисом, который будет нами последовательно опровергнут, является "ортодоксальный крест" кривых спроса и предложения применительно к рынку труда. В соответствии с данной доктриной спрос на труд представляет убывающую функцию заработной платы, а предложение – возрастающую [9]. Иными словами, рост заработной платы при прочих равных условиях приводит к снижению спроса на труд и к росту предложения рабочей силы. Схематично парадигма "ортодоксального креста" показана на рис. 1.
Простейшие логические рассуждения создают ощущение аналитической неуязвимости подобной теоретической схемы. Однако ниже будет показано, что даже "при прочих равных условиях" ортодоксальный крест на рис. 1 принципиально искажает реальные процессы, протекающие на рынке труда [2]. Важность же правильного понимания направленности кривых спроса и предложения определяется не только основополагающим теоретическим характером данной схемы, но и ее прикладными следствиями, имеющими политическую окраску. Так, например, в [9] отмечается, что трудовая модель "ортодоксального креста" широко используется за рубежом в дискуссиях между работодателями, правительством и профсоюзами по поводу заработной платы. Опираясь на схему рис. 1, работодатели обычно утверждают, что всякое повышение заработной платы увеличивает безработицу и, следовательно, в целом не может быть выгодно наемным работникам. Такое представление о ходе процесса условно назовем денежной иллюзией на рынке труда, ибо, как будет показано ниже, все соображения о столь разрушительных для рынка рабочей силы последствиях роста ее цены представляют не что иное, как миф.
Опровержение денежной иллюзии начнем с изучения кривой спроса на труд. Логика рассуждений такова. Спрос на труд целиком и полностью определяется производственными стратегиями предприятий: если происходит расширение производства, то спрос на рабочую силу возрастает: если производство коллапсирует, то и спрос на труд сокращается. Таким образом, вопрос заключается в том, приводит ли рост заработной платы к свертыванию производства. Если нет, то "спросовая" часть ортодоксального креста может считаться опровергнутой. Помимо этого, следует учитывать, что требования повышения заработной платы всегда происходят на фоне общего роста цен. Более того, именно непрерывный рост цен приводит к необходимости повышения зарплаты. Следовательно, в общем случае весь анализ переводится в несколько иное русло, а именно: каким образом инфляционные тенденции влияют на рост заработной платы и объемы производства. Ответ на поставленный вопрос предполагает учет "внутренних" особенностей самого производства, что и было нами сделано при выводе соотношения (4). Дальнейший анализ связан с выяснением формальных свойств данной зависимости.
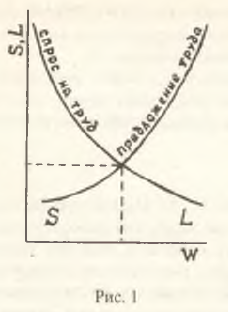
Нетрудно видеть, что зависимость X = Х(Р) в общем случае определяется знаком А и предполагает три функциональных режима (это вытекает из уравнения (3) с учетом ограничения 2Р–В>0, которое вытекает из (4) и эквивалентно рассмотрению достаточно дорогой продукции). При этом анализ показывает отсутствие у функции (4) стационарных точек. Следовательно, конфигурация экономических параметров А однозначно определяет производственную стратегию предприятия. Примечательно, что решение о расширении (сокращении) производства не зависит от знака конфигурации В и, следовательно, от эластичности материальных затрат по ценам реализации (то есть от параметров ζ и η); последние выступают в качестве пассивных факторов, которые либо усиливают, либо ослабляют формирующуюся тенденцию выпуска. Возможные режимы производства представлены на рис.2.
Учитывая L=тХѱ получаем, что спрос на труд в условиях инфляции также полностью определяется конфигурацией А и его траектории аналогичны траекториям, изображенным на рис.2. В явном виде функция спроса на рабочую силу выражается соотношением
L = mμѱexp(ѱA/2)[Р + (В/2)lп(2Р – В)] (5)
При А>0, где φ>0 (не исключена и возможность φ>1) кривая спроса на труд на рис. 1 будет восходящей и, следовательно, спросовую часть ортодоксального креста можно считать опровергнутой. Содержательно это означает, что при росте цен и заработной платы предприниматель все–таки будет наращивать производство и привлекать дополнительную рабочую силу, если он находится в относительно благоприятной ценовой и технологической среде и обладает достаточной "жадностью" в отношении ожидаемых прибылей (Е>0).
Очевидно, что все сказанное справедливо и для макрослучая. Общая картина зависит от того, из каких предприятий состоит экономика: если в ней доминируют фирмы, практикующие экспансионистские производственные стратегии, то совокупный спрос на труд будет расти. Кроме того, вся экономика может рассматриваться как одна условная фирма, для которой характерны все выявленные эффекты.
Теперь рассмотрим другую часть ортодоксального креста, связанную с кривой предложения труда. На наш взгляд, здесь уместны некоторые теоретические аналогии с денежным рынком. Так, в кейнсианской теории общий спрос на деньги распадается на две составляющие: трансакционную и спекулятивную [10]. При этом действительно гибкой, зависящей от процента, является лишь спекулятивная часть спроса. Примерно то же самое можно утверждать в отношении предложения рабочей силы S, которое определяется, с одной стороны, чисто демографическими факторами, не зависящими от текущих ценовых сдвигов, а, с другой – изменением заработной платы: S = S1 + S2(W). Тогда изменение предложения труда во времени выражается формулой
dS/dt = ∂S/∂t + (dS/dW)(dW/dt) (6)
где общий прирост спроса распадается на первичный прирост (первый компонент в правой части уравнения) и индуцированный прирост (второй компонент правой части). При этом первичный прирост показывает автономную модификацию поведения наемных работников под воздействием фактора времени, а индуцированный прирост характеризует сдвиги в величине предложения под воздействием "внешнего" фактора – цены труда. В координатах (S, W) такие сдвиги отображаются не путем простого перемещения вдоль кривой предложения S=S(W), а путем перемещения по различным кривым семейства кривых предложения с предварительным перескоком с одной кривой на другую (каждому моменту времени соответствует своя кривая из указанного семейства).
Предложение S1, обусловленное прошлой демографической волной рождаемости, жестко лимитирует верхний и нижний пределы рабочей силы на рынке труда. Предложение S2, связанное с текущими социально–экономическими сдвигами, представляет собой квазимаргинальную кадровую группу, которая гибко реагирует на изменение реальной оплаты труда. Это в основном семейные женщины, работоспособные пенсионеры, учащиеся и другие лица, которые в определенные моменты могут активизироваться на рынке труда в поисках работы. Понятно, что, хотя подобный кадровый резерв может достигать значительных размеров, вряд ли он может быть быстро задействован в производстве (или, наоборот, выведен из него). По–видимому, в краткосрочном периоде фактор заработной платы не может существенно сдвинуть массу квазимаргиналов в ту или иную сторону. Скорее лишь устойчивые долговременные (своего рода "вековые") сдвиги в уровне жизни и оплаты труда могут сформировать ту или иную степень трудовой активности населения. Однако в любом случае, если имеют место рецессивные демографические отголоски, волна сокращения рабочей силы может перекрыть незначительный прирост квазимаргиналов.
Учитывая сказанное, предложение рабочей силы если и может увеличиваться в ответ на повышение заработной платы, то в весьма ограниченном диапазоне. Следует также иметь в виду, что прилива рабочей силы можно ожидать в основном только при (φ>1. При φ<1 велика вероятность, что ∂D/∂W<0 и кривая предложения на рис. 1 будет убывающей.
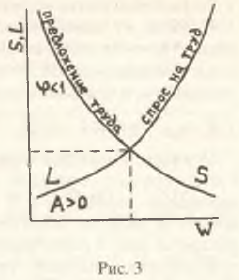
Таким образом, возможны ситуации, когда кривая предложения труда становится нисходящей, принимая вид своего зеркального отражения в ортодоксальном кресте, и, следовательно, вся идеология "креста" чрезмерно упрощена, в большинстве случаев дает неправильное представление о закономерностях возникновения безработицы. Схематично "перевернутый" крест кривых спроса и предложения труда изображен на рис. 3.
Стимулирующая и рестриктивная функции налога на добавленную стоимость
Формальный анализ формулы (4) позволяет сделать ряд качественных выводов в отношении влияния налоговых ставок на производственную активность экономической системы.
Во-первых, в условиях инфляции налог на прибыль оказывается нейтральным по отношению к производственным стратегиям фирм – объемы производства не зависят от величины ставки данного налога. Налог на добавленную стоимость, напротив – один из непосредственных рычагов регулирования производственной активности предприятий.
Кратко прокомментируем полученный на первый взгляд парадоксальный результат. Дело в том, что при более тщательном рассмотрении сущности налога на прибыль легко убедиться, что он выполняет преимущественно фискальную функцию. Действительно, налог на прибыль "отрезает" часть выручки предприятия, которая отражает чисто финансовый аспект его деятельности и в условиях роста цен весьма неоднозначно связана с объемом выпускаемой продукции. Кроме того, с точки зрения хозяйственного учета налог на прибыль является "слабым" налогом, так как на практике путем расширения статей затрат с помощью соответствующих бухгалтерских проводок прибыль фирмы может сводиться фактически до нуля. Добавленная стоимость в функциональном смысле более жестко привязана к объему хозяйственных операций и уклоняться от налога на нее, как правило, значительно сложней.
Во-вторых, влияние налога на добавленную стоимость на уровень деловой активности в общем случае описывается параболической зависимостью типа кривой Лаффера, то есть существует предел налогового пресса, который может выдержать производитель, не меняя своей стратегии выпуска.
В-третьих, эффективность налоговых послаблений зависит от общего состояния экономики; в некоторых случаях либерализация ставок налога на добавленную стоимость уже не может изменить рецессивных производственных стратегий фирмы. Однако в любом случае стимулирующая роль налоговых регуляторов весьма ограничена, так как, с одной стороны, диапазон возможных изменений налоговых ставок на практике является достаточно узким, а, с другой – эффективные либеральные сдвиги в налоговой политике носят одноразовый характер в том смысле, что существенное уменьшение налоговых ставок, как правило, возможно не более одного раза.
Рассмотрим более подробно сформулированные тезисы.
Первый из выводов вытекает непосредственно из соотношения (4) с учетом параметрических комбинаций А и В. Второй тезис следует из возможности изменения знака производной dX/dP при изменении ставки β. Точка перегиба β* вытекает из условия А = 0 и задается соотношением:
β* = 1 – тnφѱ(1 – φ)/[E – 1 + abηζ(ζ – E)] (7)
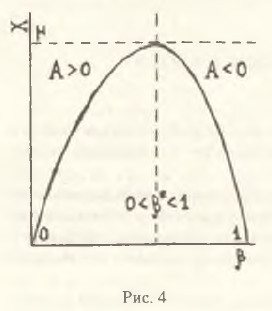
Понятно, что если в начальный момент времени А>0, то пробегание β значений от 0 до 1 приведет к кривой, изображенной на рис. 4. При этом должно выполняться априорное условие 0≤β≥1. В этой связи не исключена возможность, когда β* выйдет за пределы допустимых значений. В этом случае "обычная" производственная кривая на рис. 4 растягивается либо влево, либо вправо по оси абсцисс (возможные деформации искомой кривой показаны на рис. 5). Анализируя варианты расположения точки β* следует признать, что ситуация β*>1 в нормальных рыночных условиях представляется нереалистичной. Даже при сверхальтруистичном поведении производителя вряд ли можно надеяться, что при завинченном до упора налоге на добавленную стоимость будет иметь место максимальный выпуск (данный вырожденный случай на рис. 5 отмечен штриховкой). И, наоборот, случай β*<0 по-видимому имеет экономический смысл, свидетельствуя о том, что в определенные моменты в системе могут складываться такие условия, когда никакое снижение налога на добавленную стоимость не сможет предотвратить начавшегося производственного коллапса; смягчение налоговых ставок может лишь несколько замедлить темпы падения производства. Идентификация подобного режима функционирования экономики весьма полезна, так как позволяет вовремя переключить усилия государства с неэффективных методов налогового регулирования на иные макрорычаги, способные оживить деловую активность в стране.
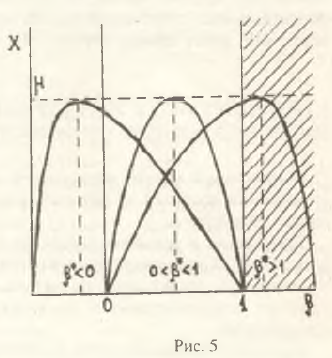
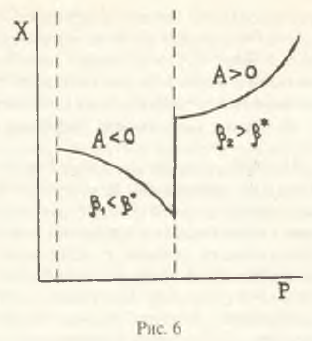
Отсюда вытекает простая схема действия налога на добавленную стоимость как стимулятора производства в условиях инфляции. Так, например, если А <0 и выпуск постепенно сворачивается, то, изменив налоговый климат, можно "качнуть" систему так, что она выйдет из рецессивного режима на траекторию устойчивого роста. В этом случае начальное значение β1, должно быть изменено до уровня β2; при этом β1>β*>β2. Количественная оценка β* позволяет рассчитать необходимое смещение налоговых ставок для получения желаемого результата. Графически схема переходного процесса при уменьшении налоговых изъятий представлена на рис.6. Рестриктивный эффект от увеличения ставки налога на добавленную стоимость аналогичен.
Формула (4) позволяет получить в явном виде соотношение для эластичности цен по налогу на добавленную стоимость σ=(β/P)(dP/dβ), которое показывает степень инфлятогенности данного налога.
Фискальные эффекты. Модификации кривой Лаффера
В настоящее время концепция кривой А.Лаффера в современной теории налогов играет центральную роль. Однако опыт показывает, что в данной области существует ряд нюансов, часто упускаемых из виду многими специалистами. В этой связи, прежде чем рассмотреть некоторые особенности действия фискальной системы в условиях инфляции, сделаем ряд предварительных замечаний, которые нам представляются исключительно важными.
Во-первых, кривая А.Лаффера была введена в экономическую науку, вообще говоря, догматически. Так, например, в [11] справедливо отмечается, что согласно некоторым современным представлениям кривая Лаффера – всего лишь логическое предположение о том, что налоговые доходы государства будут максимизированы при некоторых уровнях ставок налога в интервале от нуля до 100%. В этой связи из-за важности рассматриваемого вопроса возникают две задачи: 1) необходимость теоретического доказательства наличия кривой Лаффера хотя бы для отдельных видов налогов с выявлением условий ее существования: и 2) идентификация конкретных экономических условий с точки зрения возможных перегибов в бюджетной кривой и установление, на какой ветви этой кривой находится экономика. В данном разделе мы сосредоточимся только на теоретическом анализе геометрической формы фискальных поступлений в зависимости от ставок налогов на прибыль и на добавленную стоимость.
Во-вторых, известная кривая А.Лаффера в своей изначальной трактовке приложима к сумме налоговых сборов и соответственно задается в координатах "налоговые поступления – налоговая ставка". Хотя в основе этой концепции лежит представление о зависимости налоговой базы от величины ставок налогов, вид кривой Лаффера в общем случае на объемы производства не распространяется. Тем не менее выше было показано, что реакция производителей на изменение налоговых ставок в условиях роста цен описывается аналогичной кривой (в нашем случае это касается только налога на добавленную стоимость). В современной расширенной трактовке зависимость Лаффера, на наш взгляд, можно естественным образом распространить и на налоговую базу; в этом случае она задается в координатах "объем производства – налоговая ставка".
B-третьих, кривая Лаффера имеет макроэкономическую направленность и, строго говоря, применима не к отдельным видам налогов, а к некоему усредненному совокупному налогу. Более того, кривая Лаффера относится к усредненной налоговой системе, которая представляет собой агрегат двух налоговых подсистем с различными субъектами налогообложения – юридическими и физическими лицами. В современной научной литературе кривая Лаффера распространяется на обе налоговые подсистемы и проверяется для каждого отдельно взятого налога (см. [2], [3]). Этот же подход используется и нами.
В-четвертых, макроэкономическая постановка фискальной задачи приводит к тому, что кривая Лаффера автоматически подразумевает пропорциональный налог; более сложные фискальные системы, построенные по принципам прогрессивного или регрессивного налога, в агрегатных построениях не рассматриваются. В противном случае налоговая система характеризовалась бы двумя фискальными параметрами, что в ряде случаев может опровергнуть выводы, справедливые для пропорционального налога (в соответствии с нелинейным налогом, рассматриваемом в [2], отчисления от добавленной стоимости имеют вид: Т=β(РХ–CR)ω, где ω ≠ 1).
В-пятых, зависимость Лаффера оперирует с номинальными налоговыми поступлениями. Отсюда вытекает, что концепция кривой Лаффера применима лишь к безынфляционной экономике (или, по крайней мере, к экономике с весьма низким уровнем инфляции). В условиях же серьезных сдвигов в уровне цен налоговые поступления почти всегда будут возрастать за счет инфляционной составляющей даже при значительном сокращении налоговой базы (здесь имеет место аналогия реальных фискальных сборов с реальной прибылью предприятий). Таким образом, в инфляционной среде целесообразно рассматривать зависимость Лаффера применительно к реальным налоговым поступлениям, то есть скорректированным на темпы инфляции. Данный подход будет развит ниже и, насколько известно, такая модификация кривой Лаффера раньше не рассматривалась.
Перейдем к формальному описанию фискальных эффектов. В нашей схеме номинальные налоговые сборы Т0 от деятельности фирмы имеют вид: T0= –αWL+(β+α–αβ)(PХ–CR). Введя структурный показатель r=π/LW, данное соотношение можно переписать в более подходящем для анализа виде:
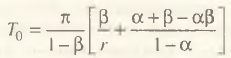 (8)
(8)
Отсюда легко получить условие для dT0/dP = 0, которое определяется степенью чувствительности объемов производства к изменениям цен. Если ρ=(Р/Х)(dX/dP), то стационарное условие обеспечивается при
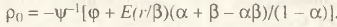 (9)
(9)
Учитывая положительность всех показателей правой части соотношения (9) приходим к выводу, что рост цен приводит к убыванию номинальных бюджетных доходов только при падающем производстве (маловероятный случай, когда Е<0, рассматривать не имеет смысла). Причем темпы этого падения должны быть достаточно высокими, что и показывает формула (9). Данный вывод представляется достаточно очевидным и отражает тот простой факт, что прирост доходов бюджета в текущих ценах может иметь место и при сокращении выпуска. Более интересная ситуация характерна для реальных налоговых поступлений Т=T0/Р. В этом случае нижняя граница эластичности выпуска по ценам задается соотношением
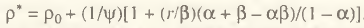 (10)
(10)
Так как р0<0 и второе слагаемое в правой части (10) всегда положительно, получаем неоднозначную ситуацию в отношении ρ˃˂0. Это означает, что ρ* может быть больше нуля и реальные бюджетные доходы будут убывать даже при расширении производства, если ρ<ρ*. Взаимное расположение точек ρ0 и р* приведено на рис.7. Обычной штриховкой показана область возрастания номинальных бюджетных доходов, а двойной – реальных.
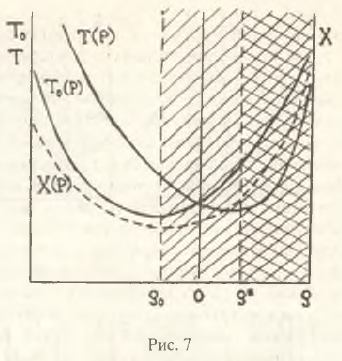
На первый взгляд, подобная ситуация кажется парадоксальной, так как увеличивающийся выпуск должен вести к расширению налоговой базы и, соответственно, к росту реальных фискальных поступлений. Однако на самом деле здесь имеет место смешение понятий объемов производства и налоговой базы. Действительно, возможны случаи, когда рост объемов реализованной продукции отстает от роста финансовых затрат предприятия. Так, например, если скорость увеличения материальных затрат обгоняет темпы расширения валовой выручки, то уменьшается реальная величина добавленной стоимости, приводя к сокращению налоговой базы и реального налога на добавленную стоимость. Если же прирост затрат на оплату труда опережает прирост добавленной стоимости, то сжимается реальный объем прибылей и реальная величина получаемого с нее налога.
Полученный результат достаточно важен с точки зрения фискального регулирования. По сути дела, он существенно корректирует экономическую доктрину предложения, которая служит теоретическим каркасом кривой Лаффера. Действительно, в соответствии со взглядами сторонников теории предложения в условиях бюджетного кризиса целесообразно несколько "отпустить" налоговые ставки, что будет способствовать расширению деловой активности, росту производства и налоговых поступлений. Однако в соответствии с нашим выводом подобные мероприятия могут оказать губительное влияние на реальную "покупательную способность" бюджета, если имеет место высокозатратная экономика с опережающим вовлечением факторов производства (то есть ѱ>1 и η>1).
В подобном случае, как это ни парадоксально, с точки зрения бюджетной эффективности не следует проводить слабую стимулирующую политику; значительно выгодней осуществить постепенное технологическое перевооружение производства в рамках фазы экономической стагнации. Если же правительство выбрало курс на повышение деловой активности, то управляющие воздействия должны быть такими, чтобы эластичность производства по ценам была достаточно высока: ρ>ρ*. Оговоримся, что наши выводы приходят в определенное противоречие с позициями представителей концепции предложения только для некоторых переходных (маргинальных) состояний экономики; в обычных случаях качественные выводы совпадают.
Дальнейший формальный анализ бюджетной кривой проводить не будем в силу его чрезвычайной громоздкости и малой наглядности. Заметим лишь, что влияние ценовых сдвигов на характер траектории кривой реальных бюджетных доходов в общем случае весьма неоднозначно. Так, например, если ввести структурный показатель доли заработной платы в величине добавленной стоимости g = WL/(PX – CR), то условие стационарности примет вид:
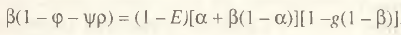 (11)
(11)
Учитывая, что эластичность производства по ценам ρ = АР2(2Р–В)-1, и предполагая достаточную устойчивость показателя g, нетрудно видеть, как условие (11) превращается в квадратное уравнение относительно Р: АР2–ρ*(В–2Р)=0. В общем случае Р0=ρ*/А и корни уравнения равны 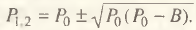 Возможный вид бюджетной кривой и ее вероятные сдвиги вдоль оси цен в зависимости от значений конфигураций А и В показан на рис. 8.
Возможный вид бюджетной кривой и ее вероятные сдвиги вдоль оси цен в зависимости от значений конфигураций А и В показан на рис. 8.
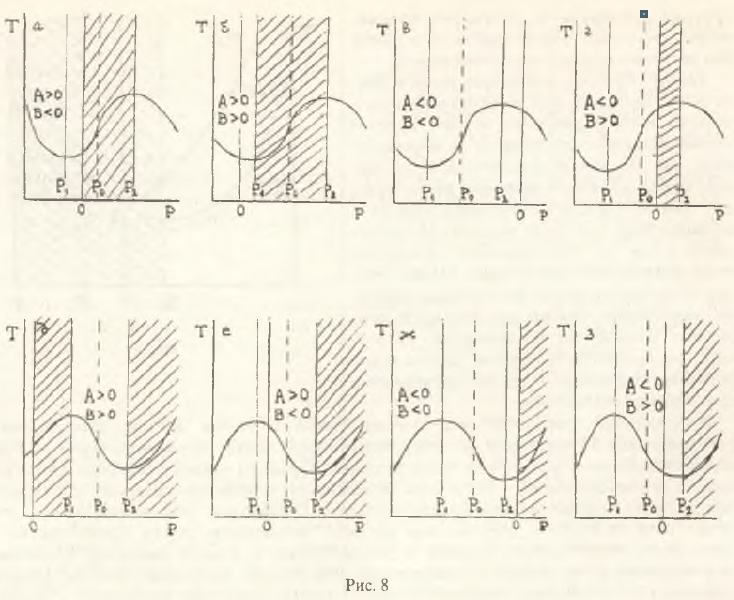
Проведенный качественный анализ убедительно свидетельствует о том, что фискальные эффекты в условиях инфляции значительно сложней производственных эффектов. Это естественно, так как бюджетные поступления зависят от налогового климата, структуры затрат в экономике и самих производственных стратегий фирм. Влияние инфляции на реальные доходы бюджета в определяющей степени зависит от того, на какой ветви искомой кривой находится экономика (см. рис.8). Интересно, что с формальной точки зрения для производственных стратегий фирм определяющее значение имеет только параметрическая комбинация A, в то время как для фискальных эффектов активную роль начинает играть и конфигурация В. Что касается роли налоговых ставок в фискальном регулировании, то строгий формальный анализ здесь весьма затруднен. Однако на качественном уровне можно утверждать следующее.
Во-первых, оба регулятора (налог на прибыль и налог на добавленную стоимость) являются значимыми для бюджетной стратегии государства. Во-вторых, зависимость бюджетных поступлений от изменений величины налоговых ставок в частном случае описываются стандартной кривой Лаффера. Однако в более сложных ситуациях влияние налоговых ставок неоднозначно, то есть могут иметь место перегибы в бюджетной кривой. Это означает, что в условиях инфляции традиционная кривая Лаффера деформируется и усложняется, отражая нетривильные эффекты в условиях инфляции. При этом влияние налога на добавленную стоимость оказывается более сложным и неоднозначным, чем влияние налога на прибыль. В-третьих, точки перегиба на бюджетной кривой (следуя [12] будем называть их точками Лаффера), оказываются величинами принципиально непостоянными в условиях роста цен. Как правило, точки Лаффера "плавают" в зависимости от уровня цен.
Контуры более общего случая
В данной работе мы рассматривали только два вида налога: на прибыль и на добавленную стоимость. На практике число налоговых регуляторов неизмеримо больше. Особый интерес представляют собой налоги и начисления на заработную плату γ, а также экспортные θ и импортные λ тарифы, регулирующие объемы внешнеэкономических операций. При этом экспортные тарифы распространяются непосредственно на объем продаж предприятия-экспортера, соответствующим образом уменьшая величину его выручки, а импортные пошлины ложатся на затраты, производимые фирмами-импортерами, увеличивая их массу. В этом случае чистая прибыль производителя задается выражением
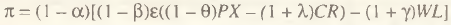 (12)
(12)
где ɛ – валютный курс. Если фирма является чистым экспортером, то формула (12) принимает вид: .png) ; если рассматривается чисто торговая фирма-импортер, то (12) имеет вид: π=(1–α)[(1–β)(РХ–ɛCR(1+λ))–(1+γ)WL].
; если рассматривается чисто торговая фирма-импортер, то (12) имеет вид: π=(1–α)[(1–β)(РХ–ɛCR(1+λ))–(1+γ)WL].
Для изучения роли каждого налога можно использовать ту же самую схему, что и ранее. Однако и без специального анализа ясно, что все налоги, за исключением налога на прибыль, в условиях инфляции являются значимыми регуляторами объемов производства. При этом существенную роль в государственном регулировании начинает играть факт сильной взаимозависимости различных видов налоговых изъятий. При принятых нами допущениях получается, что налог на прибыль, будучи нейтральным по отношению к производственным стратегиям фирмы, одновременно как бы "позволяет" задействовать в полной мере все остальные фискальные рычаги. Среди последних только тарифы на экспортируемую продукцию представляют прямой регулятор объемов производства, в то время как прочие налоги могут быть отнесены к косвенным макроэкономическим рычагам (указанная классификация налогов не имеет ничего общего с классификацией, данной в [5]).
* * *
Мы попытались продемонстрировать чрезвычайную сложность теории налогов, и показать нетривиальный характер фискальных закономерностей в инфляционной среде. Однако полученные конкретные результаты нельзя переоценивать, так как в анализе использовался целый ряд предпосылок, сильно огрубляющих реальные процессы. Так, например, все результаты распространяются только на короткие временные интервалы, показывая лишь общую направленность тех или иных экономических сдвигов. При этом нами не учитывалось активное ограничивающее влияние на производство со стороны спроса. Вместе с тем спросовый зажим экономики может существенно трансформировать предполагаемый ход событий.
Другое важное допущение – жесткая технологическая связь между затратами и выпуском. Такая жесткость на практике, как правило, сильно размывается гибкостью системы бухгалтерского учета. Это связано как с возможностью взаимного перелива финансовых средств по статьям расходов, так и с возможностью "накачки" самих расходных статей с целью сокращения налоговой базы. Это означает существование определенной эластичности между различными видами затрат, что невозможно учесть, оставаясь в рамках простых аналитических схем.
Наконец, огромное значение имеет политика предприятий, которая отнюдь не ограничивается манипулированием выпуска и затрат. Так, например, та или иная дивидендная стратегия фирм с акционерной формой собственности может приводить к искажению классических стратегий, рассмотренных нами. В этом случае меняется само понятие чистой прибыли и осложняется формализация целевых установок фирмы. Разумеется, за рамками статьи остается вопрос о влиянии роста налоговых ставок на интенсивность процесса уклонения предприятий от налогов путем перехода в теневой сектор экономики.
Литература
[1] С.В. Алексашенко, Д.А. Киселев, П. М. Теплухин, Е. Г. Ясин. Налоговые шкалы: функции, свойства, методы управления ("Экономика и математические методы". Т. XXV. Вып. 3. 1989).
[2] Л. Е. Соколовский. Подоходный налог и экономическое поведение (введение в литературу) ("Экономика и математические методы". Т. XXV. Вып. 4, 1989).
[3] Л. Е. Соколовский. Налог на добавленную стоимость и предприятие, максимизирующее прибыль ("Экономика и математические методы". Т. 28, Вып. 4, 1992).
[4] С.М. Мовшович, Л.Е.Соколовский. Выпуск, налоги и кривая Лаффера ("Экономика и математические методы". Т. 30. Вып. 3, 1994).
[5] И. В . Ф е д о р о в а. Реформирование системы налогообложения предприятий в России (автореферат дис. ... канд. экон. наук. М., 1995).
[6] М . И н т р и л и г а т о р. Математические методы оптимизации и экономическая теория. М.. 1975.
[7] Е . В . Б а л а ц к и й. Дифференциальные свойства кривых спроса и предложения ("Мировая экономика и международные отношения". N 12. 1995).
[8] И. Н. Бронштейн. К.А. Семендяев. Справочник по математике для инженеров и учащихся втузов. М., 1986.
[9] А. В. Каше нов. В.В.Трубин, С.С.Утинова. Рынок труда в России: проблемы формирования и регулирования. М.. 1995.
[10] Л . Харрис. Денежная теория. М., 1990.
[11] К. Р. Макконнелл, С.Л.Брю. Экономикс: принципы, проблемы, политика. М., 1992.
[12] С. В. Гусаков, С. В.Жак. Оптимальные равновесные цены и точка Лаффера ("Экономика и математические методы". Т. 31, Вып. 4, 1995).
[1] В этом случае разложение, например, заработной платы по формуле Тейлора с точностью до первого члена ряда в точке W0=1 при W>>1 выглядит следующим образом: W=nРφ ≈nφ(P–1)≈nφР [8].
[2] Отметим любопытный факт: подавляющее большинство теоретических схем, использующих аппарат кривых спроса и предложения, графически изображается таким образом, что по оси абсцисс откладываются объемы спроса и предложения, а по оси ординат – цена [9]. При такой интерпретации зависимой переменной оказывается цена, а спрос и предложение выступают в качестве ее факторообразующих элементов. Но тогда получается совершенно иная аналитическая схема, не имеющая никакого отношения к кривым спроса и предложения. Сейчас трудно определить, кто родоначальник подобной аналитической некорректности. Важно другое: возникший логический казус с удивительным постоянством продолжает воспроизводиться в работах как отечественных, так и зарубежных авторов.
Официальная ссылка на статью:
Балацкий Е.В. Фискальное регулирование в инфляционной среде// «Мировая экономика и международные отношения», №1, 1997. С.32–44.