Функционирование каждой экономической системы происходит в соответствии с характерными для нее фундаментальными принципами. Однако экономические принципы и законы не имеют абсолютного характера и выполняются лишь при вполне определенных условиях. Тем не менее этот аспект проблемы практически полностью выпадает из экономической теории. Цель статьи – попытка определить сферы реализации некоторых базовых экономических принципов. Другими словами, будут рассмотрены те маржинальные (предельные) границы экономических рынков, за рамками которых рассматриваемые нами законы недействительны. Методология анализа состоит в установлении характера дихотомии различных режимов функционирования экономических систем с использованием традиционных макро– и микроэкономических положений.
Несмотря на то, что на сегодняшний день сформулировано немало различных экономических принципов и законов, их модельный и содержательный синтез пока не осуществлен. В этой связи целесообразно рассмотреть некоторые из них в рамках единой теоретической схемы, основанной на принципах равновесия и маржинализма.
Монетарные ограничения закона Сэя
В качестве центрального звена, связывающего предельные свойства экономических систем в единую теоретическую схему, мы будем рассматривать закон Сэя. Его сущность заключается в том, что предложение порождает свой собственный спрос [1]. Однако для дальнейшего системного анализа экономических процессов необходима формализация данного принципа. В своей классической ("сильной”) формулировке закон Сэя можно записать в дифференциальной (приростной) форме: ∂Ȳ/∂Y=1, где Y – спрос на товары, выраженный в денежных единицах; Ȳ – стоимостная оценка наличной товарной массы (предложения). В случае, когда величины спроса и предложения используются в натуральном исчислении (D и S, соответственно), то классическая концепция закона Сэя для них может быть выражена как; ∂D/∂S=1. Данное соотношение автоматически вытекает из хорошо известного тождества Сэя, согласно которому совокупный спрос на все товары равен их совокупному предложению: Ȳ=Y [2]. Аналогичная ситуация характерна и для натуральных показателей, так как Y=PS, Ȳ=PD, где Р – отражает средний уровень цен.
С финансовой точки зрения закон Сэя достаточно очевиден: произведенный и реализованный продукт приводит к возникновению соответствующего дохода у производителя, который в денежной форме представляет собой не что иное, как платежеспособный спрос. Таким образом, переход предложения в спрос есть результат процесса, когда ’’продукты обмениваются на продукты” (Ж.Б. Сэй) [1]. С этой точки зрения закон Сэя автоматически вытекает из так называемой ’’догмы” Смита, в соответствии с которой все денежные средства в экономике представляют собой доходы [2]. Более тонкий анализ связан с учетом действия дополнительных факторов, которые также увеличивают совокупный спрос. Подобные эффекты возникают благодаря существованию в экономической системе комплементарных (взаимодополняемых) товаров. Это приводит к тому, что увеличение объемов производства определенных товаров посредством сложной цепочки рыночных взаимосвязей создает потребность в расширении производства соответствующих комплементарных благ. Кроме того, из схемы межотраслевых взаимодействий вытекает, что выпуск нового товара, как правило, вызывает необходимость развития смежных производств. Уже сами по себе перечисленные эффекты, порождая лавину спроса как в сферах производства и обращения, так и в сфере потребления, способны приводить в действие закон Сэя. Однако очевидно, что записанные выше дифференциальные соотношения на деле являются слишком жесткими. В частности, при сохраняющемся в течение некоторого времени неравновесии на товарном рынке (то есть Ȳ=μY), закон Сэя в ’’сильной” форме не выполняется и может быть записан в следующей ’’слабой” (менее категоричной) форме: ∂Ȳ/∂Y>0. Такая форма записи является естественным обобщением закона Сэя по сравнению с его ’’сильной” формой. Содержательно это может соответствовать ситуации, когда не весь произведенный продукт оказывается реализован. Для физических объемов спроса и предложения характерна аналогичная ситуация: ∂D/∂S>0.
Переход к ” слабой” форме закона Сэя обусловлен тем, что его ’’сильная” форма, а, следовательно, и тождество Сэя, противоречит более общему экономическому принципу – закону Вальраса, что не позволяет использовать его в дальнейших теоретических построениях; ’’слабая” форма это противоречие снимает. Что касается закона Сэя в ’’слабой” форме, то, на первый взгляд, кажется, что он выполняется всегда, так как параметр µ с экономической точки зрения не может быть меньше, нуля. Однако ниже будет показано, что при встраивании в общую схему денежной теории, выполнение закона Сэя в общем случае сопряжено с достаточно жесткими монетарными условиями.
Рассмотрим взаимодействие денежного и товарного рынков, которое формально можно представить тождеством JI. Вальраса в следующей агрегированной форме: (M̅–М)=(Y–Ȳ), где M̅ – спрос на деньги; М – фидуциарные активы, то есть фактическая величина денежной массы, обращающейся в экономической системе [2]. Здесь и далее мы не будем рассматривать денежные и другие финансовые средства; для наших целей вполне достаточно рассматривать однородную массу денег, поток которых обеспечивает операции на открытом рынке. Приведенное тождество соответствует закону Вальраса, согласно которому сумма избыточного спроса на товарных и денежном рынках равна нулю [2].
В несколько иной форме взаимодействие товарного и денежного рынков описывает уравнение И. Фишера VM=V, где V – скорость обращения денег [2]. С методологической точки зрения закон Вальраса, тождество Сэя и уравнение Фишера являются простыми балансовыми соотношениями, отражающими идею общего равновесия в экономике. При комбинировании уравнения Фишера и тождества Вальраса можно получить чрезвычайно важную формулу:
∂Ȳ/∂Y = 1 + 1/V – ∂M̅/∂Y (1)
Из соотношения (1) вытекает монетарное условие, определяющее границы инвариантности закона Сэя и тем самым очерчивающее экономическую область, в которой он выполняется, а именно: ∂M̅/∂Y<1+k (k = 1/V – коэффициент Маршалла). На рис.1 штриховкой показана область, где закон Сэя нарушается, иллюстрируя принципиальное значение полученной дихотомии. Дополнительных комментариев требует область, где ∂M̅/∂Y<0. Такое состояние экономической системы представляет собой явно вырожденный случай, когда увеличение товарной массы приводит к уменьшению спроса на деньги при неизменной скорости их оборачиваемости. Очевидно, что содержательной экономической интерпретации данный случай не имеет и сказать что-либо определенное о поведении системы в указанной области нельзя. Таким образом, закон Сэя выполняется при положительной эластичности спроса на деньги по товарной массе, не превышающей величину (1 + k) [3].
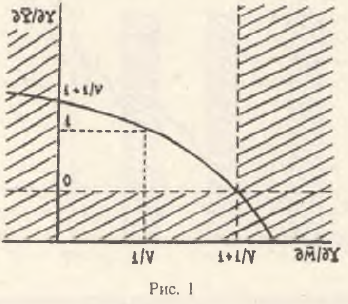
Отметим, что через формулу (1) оказываются связанными между собой такие фундаментальные экономические положения как закон Вальраса, закон Сэя и уравнение Фишера (или аналогичное ему кембриджское уравнение). Однако следует особо оговориться, что при выводе уравнения (1) использовалась гипотеза о том, что скорость обращения денег не зависит прямо от изменений объемов производства. На наш взгляд, данное допущение не является слишком сильным, так как в современных условиях скорость обращения денег зависит не столько от объемов производства, сколько от эффективности существующей денежно–кредитной системы и ее можно считать экзогенной величиной. Для простой количественной денежной теории указанное положение является одним из традиционных постулатов.
Из проведенного анализа следует, что спросовые свойства экономической системы зависят от скорости обращения денег, а уравнение (1) в явном виде задает эту зависимость. При этом выполняются следующие предельные соотношения
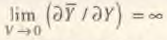 (2)
(2)
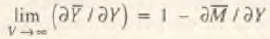 (3)
(3)
Из условий (2) и (3) следует, что по мере роста эффективности денежной системы, а, следовательно, и скорости обращения денег, действие закона Сэя ослабляется. В предельном случае (3), означающем отсутствие хранения (сбережения) денег, когда последние практически не задерживаются при проведении финансовых операций, закон Сэя выполняется в ’’сильной” форме (в форме равенства) только при неизменности спроса на деньги. Данный вывод соответствует ортодоксальной денежной теории и несколько уточняет ее результаты [2]. Действительно, столь стремительная циркуляция денег в системе приводит к непрерывным покупкам, что равносильно немедленному переходу предложения в спрос. Если же происходит частичное перераспределение совокупного спроса на денежные агрегаты (например, население начинает ориентироваться на вложение средств в облигации и акции корпораций), то это приводит к уменьшению интенсивности процесса купли–продажи товаров и, следовательно, ослабляет закон Сэя. Можно считать без потери степени общности, что спрос на деньги при бесконечной скорости их обращения не реагирует на возрастание товарной массы.
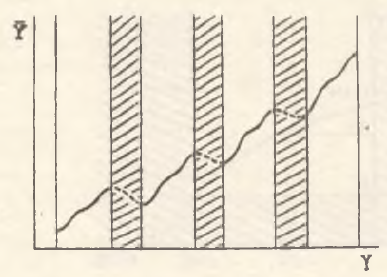
Рис 2.
Случай (2) соответствует полной тезаврации, когда эмитированные в оборот денежные средства мгновенно оседают у экономических агентов и не участвуют в их последующих сделках. В такой ситуации действие закона Сэя теоретически неограничено. Содержательно это означает, что при столь активной тезаврации денежных средств имеет место хозяйство с натуральным товарообменом, когда непосредственного приобретения экономическими агентами необходимых им продуктов не происходит; данный процесс идет посредством промежуточных "холостых” операций обмена. Таким образом, прежде чем конкретный товар "найдет” своего потребителя, должна сработать весьма длинная цепочка обмена. При этом неизбежно возникает спрос на соответствующие промежуточные продукты, выступающие в качестве временного средства платежа. Это означает, что в экономике возникает огромное число комплементарных благ. Так как обменная цепочка теоретически может быть сколь угодно длинной, то и действие закона Сэя оказывается бесконечно сильным. Как правило, рассматриваемый случай характерен либо для начальных стадий развития экономических сообществ, либо для хозяйств, основанных на золотомонетарном денежном эквиваленте, производство которого строго ограничено.
Чрезвычайно важен следующий аспект проводимого анализа. Если принять постулат о возможном нарушении закона Сэя, то условие (1) очерчивает монетарное ограничение его выполнения. Правда, данный вопрос является дискуссионным, так как можно предположить, что рост предложения в кризисные периоды приводит к переключению индивидуального спроса с одних групп товаров на другие, в целом сопровождаясь возрастанием совокупного спроса. Если же исходить из того, что закон Сэя в ’’слабой” форме выполняется всегда, то полученные результаты будут иметь совершенно иную экономическую интерпретацию, превращаясь в условие, характеризующее область допустимых значений эластичности спроса на деньги по объему производства. Однако, по–видимому, следует придерживаться первой трактовки: с одной стороны, у нас нет никаких статистических доказательств того, что показатель ∂M̅/∂Y не может принимать значения больше величины (1+k), а с другой, возникновение кризисных ситуаций, когда дополнительное наращивание объемов производства без радикального изменения его структуры не приводит к возрастанию совокупного спроса, соответствует нарушению закона Сэя. В таких ’’узлах” экономического развития образуются своеобразные спросовые ”ямы”. При этом возникающее в системе затоваривание с формальной точки зрения соответствует перегибам в функции совокупного спроса (схематично такие перегибы в кризисные периоды показаны на рис.2).
Закон Юма и внешнеэкономические эффекты
Выше рассматривалось такое достаточно общее свойство экономических систем, как закон Сэя. Однако последний имеет свой внешнеторговый эквивалент – закон Юма, который является частным случаем тождества Сэя [3].
Согласно закону Юма, экспорт всегда равен импорту, а следовательно, любое увеличение импорта приводит к соответствующему расширению экспорта [3]. Формально данное положение можно выразить следующим образом: ∂J/∂I = I, где J и I – соответственно объем экспорта и импорта во внутренних ценах. В случае использования физических объемов экспорта и импорта закон Юма в ’’сильной” форме запишется аналогично.
Формулируя данный закон, Д.Юм исходил из теории межстрановых переливов золота. В соответствии с данной теорией, механизм межстранового перемещения золота является средством восстановления как внутреннего, так и внешнего экономического равновесия. Общая схема механизма выравнивания внешнеторгового сальдо следующая: возникшее неравновесие во внешнеэкономических расчетах страны инициирует соответствующие приливы или отливы золота, что в свою очередь воздействует как на внутренние цены, так и на экспорт и импорт; подобные сдвиги в условиях торговли и приводят к выравниванию баланса внешних расчетов [3]. Однако очевидно, что даже в случае действия механизма межстрановых переливов золота закона Юма в ’’сильной” форме слишком категоричен. В связи с этим наряду с использованием "сильной” формы закона Юма можно использовать его ’’слабую” форму: ∂J/∂I > 0.
Теперь рассмотрим условия, гарантирующие выполнение закона Юма в ’’слабой” форме. В общем случае состояние товарного рынка с учетом внешнеторговых операций задается соотношением: Ȳ=μ(Yo+I–J), где Yo – валовой внутренний продукт страны. Используя предположение о том, что изменения объема импорта воздействуют не на величину внутреннего продукта, а лишь на его структуру, можно получить формулу:
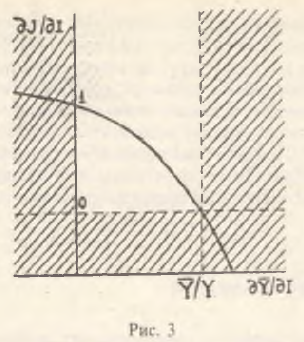
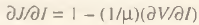 (4)
(4)
из которой следует, что закон Юма выполняется только при наличии условия ∂Ȳ/∂I<Ȳ/Y, то есть степень воздействия импорта на совокупный спрос не должна превышать дисбаланса, имеющегося на товарном рынке. Дополнительное ограничение можно получить, учтя тот факт, что эластичность спроса по импорту положительна. Обратная ситуация возможна только в случае, когда сумма внутреннего продукта и торгового баланса отрицательна, что не имеет экономического смысла. Графически область определения закона Юма показана на рис.3; штриховкой обозначена экономическая область, где закон Юма не выполняется.
Наиболее интересен и репрезентативен случай, когда товарный рынок находится в состоянии равновесия (μ=1) и возмущения со стороны импортируемых товаров не нарушают сложившегося баланса. В этом случае закон Юма в слабой форме требует следующего ограничения чувствительности совокупного спроса по импорту: ∂Y/∂I<1. Что касается закона Юма в '’сильной” форме, то, как видно из формулы (4), он выполняется только в условиях полной нечувствительности совокупного спроса к сдвигам в объеме импорта. Таким образом, даже при выполнении закона Сэя в ’’сильной” форме закон Юма требует дополнительных весьма жестких условий для реализации. Если же эффект от увеличения импорта перераспределить на другие неучтенные нами макроэкономические агрегаты (когда изменения интенсивности потока импортных товаров влияют на экономическую активность системы и приводят к сдвигам в объеме произведенного внутреннего продукта, а относительный товарный дисбаланс непостоянен), то условие сохранения действия закона Юма оказывается значительно сложнее, а его выполнение становится вообще сомнительным. Кроме того, в реальности свободные межстрановые переливы товаров сильно ограничены таможенными барьерами и, наоборот, могут интенсифицироваться протекционистской политикой государств, что сдерживает естественное проявление закона Юма. Таким образом, последний имеет значительно более ограниченный характер действия, чем закон Сэя.
Макроэкономическая теория полезности
Помимо монетарных ограничений закон Сэя имеет естественные ограничители, порождаемые сложившейся системой ценностей совокупного потребителя. Рассмотрим их более подробно.
В соответствии с субъектной теорией ценности стоимостная оценка товара определяется его предельной полезностью dU/dS, где U=U(S) – функция полезности. Показатель предельной полезности отражает величину полезного эффекта, который потребителю приносит приобретение дополнительной единицы товара [4]. Следовательно, предельная полезность представляет собой ту цену, по которой потребитель готов приобрести товар. Если указанная оценка выше фактического уровня цен, то в этом случае спрос на товарном рынке превышает наличное предложение и имеет место процесс недопотребления. В противном случае в системе формируется отрицательный избыточный спрос, а имеющееся на рынке напряжение соответствует ситуации перепроизводства и затоваривания. Если же предельная полезность совпадает с фактической ценой Р, то на товарном рынке наблюдается равновесие. Исходя из сказанного условие материально–стоимостного неравновесия можно записать как:
D/S ≡ (∂U/∂S)/(πР) (5)
В правой части (5) стоит своего рода коэффициент относительного искажения цен, в левой – фиксируется материальный дисбаланс на товарном рынке. Соотношение (5) показывает, каким образом взаимоувязаны между собой основные макроэкономические характеристики. В зависимости от целей анализа любые три переменные (5) могут рассматриваться в качестве экзогенных; оставшаяся переменная будет выступать в качестве эндогенной. Помимо характера балансировки четырех макропоказателей при работе с представленной моделью (5) следует учитывать тог факт, что каждый из них сложным образом зависит от широкого спектра дополнительных факторов [4]. Параметр π в (5) выполняет следующие функции. Во-первых, он выступает в качестве коэффициента пропорциональности; во-вторых, нормирует цены и предельную полезность в единых единицах измерения; в-третьих, вводит в рассмотрение монетарный фактор, являясь оценкой денежной массы [5].
Подчеркнем, что все используемые в (5) характеристики несут макроэкономическую смысловую нагрузку. Так, например, U = U(S) представляет собой агрегированную функцию полезности имеющейся товарной массы в отличие от микроэкономической функции полезности, которая зависит от объема потребляемых благ. Однако аналогичные рассуждения и получаемые результаты можно легко распространить и на микроуровень.
Если ввести понятие эластичности предельной полезности [4] σ=–S(U"/U') (U' и U" – производные функции полезности по S, соответственно первого и второго порядка), то из условия неравновесия (5) можно получить уравнение:
 (6)
(6)
Данное уравнение позволяет увязать в рамках единой теоретической конструкции закон Сэя и закон Госсена, который формально в нашем случае выглядит следующим образом: U"<0, то есть предельная полезность товаров (благ) уменьшается по мере того, как они производятся (потребляются) [4]. Кроме того, с помощью (6) и (1) с законом Гессена оказываются связанными закон Вальраса и закон Фишера. Таким образом, с помощью всего лишь двух простых уравнений можно достаточно эффективно описать механизм интеграции четырех основополагающих экономических принципов.
Как следует из (6), закон Сэя в слабой форме выполняется при условии: λ–σ<1. Содержательная интерпретация выведенного условия такова: закон Сэя выполняется только в том случае, если закон Гессена проявляется не слишком активно. Учитывая устоявшуюся экономическую терминологию, эластичность σ представляет собой показатель относительной антипатии к производству. Тогда смысл полученного условия можно сформулировать следующим образом: закон Сэя выполняется до тех пор, пока антипатия совокупного потребителя к производству превышает величину (1–λ). С формальной точки зрения при введении в рассмотрение параметра ω=πP(∂D/∂S) данное условие равносильно следующему простому дифференциальному уравнению:
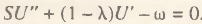 (7)
(7)
Скалярная величина ы характеризует поведение экономической системы с точки зрения выполнения закона Сэя: если ω>0. то закон выполняется в "слабой” форме; если ω=Р, он выполняется в классической ’’сильной” форме; если ω<0, то закон не выполняется. Очевидно, что в указанной трактовке уравнение (7) порождает некую функцию полезности, обладающую определенными свойствами в зависимости от возмущающего параметра ω. Таким образом, возникает принципиальная возможность построить агрегатную функцию полезности в зависимости от спросовых свойств экономической системы, что имеет самостоятельное значение в связи с важностью данной экономической категории [6].
Рассмотрим теперь ’’обратный” закон Сэя, когда спрос порождает предложение. Данный закон неявно фигурирует в экономической теории в качестве закона удовлетворения общественных потребностей и по аналогии с законом Сэя в слабой форме его можно записать следующим образом: ∂S/∂D>0. Если использовать понятие эластичности цен по спросу ѱ = (D/P)(∂P/∂D), то из модели (5) вытекает соотношение, позволяющее определить границы выполнимости закона удовлетворения общественных потребностей:
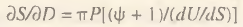 (8)
(8)
Из (8) следует, что указанный закон выполняется лишь при ѱ>–1, то есть данный экономический принцип зависит от степени гибкости цен по спросу на производимые продукты.
Учитывая, что 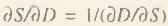 , закон удовлетворения общественных потребностей оказывается достаточно просто связанным с законом Сэя, а следовательно, и с уравнениями (1) и (6), тем самым легко встраиваясь в общую систему рассматриваемых маржинальных законов. Таким образом, три уравнения (1), (6) и (8) позволяют системно охватить пять наиболее значительных экономических принципов.
, закон удовлетворения общественных потребностей оказывается достаточно просто связанным с законом Сэя, а следовательно, и с уравнениями (1) и (6), тем самым легко встраиваясь в общую систему рассматриваемых маржинальных законов. Таким образом, три уравнения (1), (6) и (8) позволяют системно охватить пять наиболее значительных экономических принципов.
Представляется важным тот факт, что закон Сэя и закон удовлетворения общественных потребностей находятся в обратной зависимости, то есть чем сильнее проявляется один из них, тем слабее действие другого. Следовательно, данные два закона обладают свойством взаимного сдерживания, что является проявлением универсальных саморегулирующих качеств экономических систем [7].
Режимы функционирования экономических систем
Полученные выше зависимости позволяют проанализировать различные состояния, в которые могут попадать экономические системы. Данный аспект чрезвычайно важен, так как поведенческие свойства систем полностью определяются режимом, в котором они функционируют. В свою очередь функциональный режим характеризуется конфигурацией определенных макропараметров. Структура уравнения (7) такова, что конкретный вид порождаемой им функции полезности зависит от значения эластичности цен по предложению товаров. В связи с этим рассмотрим возможные варианты.
В наиболее общем случае решением уравнения (7) является зависимость, которая при ω=0 представляет собой усложненный вариант стандартной функции полезности с постоянной эластичностью [4]. Для режимов λ=1 и λ=0 решениями (7) становятся функции, являющиеся модифицированными случаями логарифмической функции Д.Бернулли [4] [7]. Таким образом, результаты работы с моделью (5) хорошо верифицируются в рамках традиционной экономической теории, отвечая основополагающим представлениям и постулатам маржинализма.
Проанализируем теперь полученные решения и некоторые экономические выводы, которые из них вытекают.
Прежде всего отметим, что зависимость U=U(S) удовлетворяет априорному свойству функции полезности (закону Госсена), то есть с учетом положительности S закон Госсена для них выполняется всегда. Несложно видеть также, что закон Госсена зависит от степени гибкости цен, причем с ростом эластичности цен по предложению товаров его действие усиливается. Такой вывод представляется достаточно естественным, так как рост производства, сопровождаемый обгоняющим ростом цен, действительно должен приводить к более быстрому убыванию предельной полезности при дополнительном увеличении наличной товарной массы.
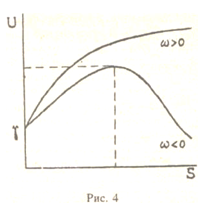
Чрезвычайно интересен вывод о том, что в случае выполнения закона Сэя функция полезности при λ≠1 монотонно и неограниченно возрастает. В противном случае, когда закон Сэя нарушается, указанная функция имеет глобальный максимум (примерный вид функции полезности для данных случаев приведен на рис.4) [8]. Такой экономический оптимум часто называется ’’центром наслаждения” или ’’блаженством” (Bliss) и за его пределами расширение производства ухудшает общественную жизнь [4]. В этой связи небезынтересно отметить, что в построениях подобного рода под полезностью иногда понимается уровень счастья, получаемого от владения богатством. В частности, П.Лаплас конкретные блага классифицировал как физическое счастье, а полезность – как духовное счастье [8]. А.Маршаллом было использовано такое понятие, как бесполезность (тягость) труда, затрачиваемого для получения определенного количества благ Н=H(S) [8]. Исходя из этой концепции состояние блаженства достигается лишь тогда, когда удовлетворение, получаемое от потребления товаров, будет равно страданию, связанному с их производством и приобретением: U=Н. Подобное состояние возможно лишь при доминировании в обществе специфических психологических установок, отражающих жесткую философию потребительской умеренности.
В реальности достижение устойчивого состояния ’’блаженства” возможно в рамках двух диаметрально противоположных типов социально–экономических сообществ. Первые представляют собой различные примитивные и деградирующие экономические формации, в которых наблюдается патологическая деформация жизненных интересов людей. В этом случае происходит ’’замораживание” возникшей ситуации, когда стабилизация спроса отражает гипертрофированную инерционность потребительских преференций индивидов. Другой тип социально–экономических сообществ характерен для преуспевающих постиндустриальных формаций, когда формируется прогрессивная, тонко сбалансированная система общественных потребностей. При этом стабилизация спроса на производимые товары сопровождается ростом требований к их качественным характеристикам. В этом случае происходит повсеместное доминирование свойства взаимозаменяемости благ: производство каждого нового более совершенного материального блага приводит к отмиранию и исчезновению одного или нескольких ’’старых” продуктов. Таким образом, производство новых товаров, происходящее на фоне активного вымывания их устаревших аналогов, ведет к прекращению разрастания товарной массы при том, что ее качественный состав может резко меняться.
Понятно, что реализация таких производственных и потребительских норм возможна лишь при весьма высоком уровне интеллектуального и духовного развития индивидов. Данные выводы тесно корреспондируют с известным положением о том, что кривая спроса на работу может стать убывающей либо в бедных странах, где потребности населения сводятся к получению жизненного минимума, либо в очень богатых странах, где доход занятых достаточно высок, чтобы индивиды поддерживали его на прежнем уровне, работая несколько меньше и пользуясь дополнительными часами досуга [1]. Такие результаты относительно рынка труда и товарного рынка гармонично дополняют друг друга. Таким образом, одним из ценных качеств модели (5) является то, что она позволяет получить определенную информацию о том, где экономическая система достигает предела расширения своего производственного потенциала.
Помимо характеристики ш весьма существенное влияние на характер кривой полезности оказывает эластичность цен λ. Чтобы установить роль данного параметра, рассмотрим его различные конфигурации с величиной ω. Наиболее интересными представляются следующие два случая.
Первый: (ω>0; λ<1). При данной комбинации параметров функция полезности возрастает. Второй: (ω>0; λ>1). При таком сочетании параметров функция полезности убывает.
Данные результаты представляют непосредственный интерес с точки зрения маржинальных режимов функционирования экономических систем. Дело в том, что в нормально функционирующей экономике рост товарной массы, вообще говоря, должен оказывать понижательное действие на цены, формируя тем самым отрицательную величину их эластичности λ. В этом случае функция полезности имеет свой естественный вид и обладает всеми априорными свойствами, характерными для нее (в частности, является неубывающей). В случае переключения знака λ с отрицательного на положительный существенной трансформации системы ценностей потребителей не происходит лишь при λ<1. В случае, если эластичность цен превышает указанное пороговое значение, функция полезности претерпевает принципиальные деформации вплоть до потери одного из основных своих свойств – свойства возрастания (аксиомы ненасыщения). Иными словами, парадоксальная ситуация, когда λ>0, является устойчивой с точки зрения системы ценностей совокупного потребителя лишь до точки перегиба λ=1, за пределами которой происходит разрушение сложившихся потребительских предпочтений. По-видимому, в экономической области λ>1 либо начинают действовать весьма сложные неравновесные законы, либо система оказывается в состоянии устойчивого кризиса.
Что касается функции полезности, когда λ=1, то она представляет особый интерес. Данный случай соответствует своеобразному инвертированию содержательного смысла условия λ–σ<1. Последнее иллюстрирует естественный ограничитель закона Сэя, обусловленный характером агрегированной функции полезности и выполнением закона Госсена, в то время как при λ=1 имеем случай, когда закон Сэя может выполняться лишь при одновременном нарушении закона Госсена. Стабилизация системы потребительских ценностей возможна лишь при однозначном нарушении закона Сэя. Таким образом в рассматриваемом экономическом режиме функция полезности имеет смысл лишь при ω<0, обладая при этом точкой насыщения; закон Госсена в данном случае сохраняется.
Более простые случаи функциональных режимов экономических систем возникают при рассмотрении закона удовлетворения общественных потребностей. В частности, при ѱ>–1 данный закон выполняется. Данный режим типичен (нормален), так как в реальности он наблюдается почти всегда. Это связано с тем, что эластичность, как правило, больше нуля, ибо при автономном росте спроса на товары цены имеют тенденцию к увеличению. Примечательно, что даже если ѱ<0, то с точки зрения нарушения закона удовлетворения общественных потребностей система обладает определенным запасом прочности, то есть степень ’’извращенности” реакции цен на сдвиги в уровне спроса должна быть весьма высока. Нарушение названного закона происходит при ѱ<–1. Такое условие является аномальным и соответствует ’’сверхгиффиновскому” макроэффекту. В реальности подобная ситуация практически никогда не возникает. В случае ѱ=–1 экономическая система глобально нейтральна. Данное состояние крайне неустойчиво и характеризуется тотальным сбоем в хозяйственном механизме системы. Сила, с которой проявляется закон удовлетворения общественных потребностей, зависит также от степени относительного расхождения между величиной предельной полезности и уровнем цен.
Теперь попытаемся несколько обобщить полученные результаты. Так, например, при ’’слиянии” соотношений (6) и (8) можно получить следующее уравнение, задающее семейство кривых полезности:
SU" + [(1 – λ) – 1/(1 + ѱ)]U' = 0. (9)
Отсюда автоматически получаем компактный и вместе с тем максимально общий вид агрегированной функции полезности с постоянной эластичностью (обозначим θ=λ+1/(1+ѱ); β и γ – константы, зависящие от начальных условий)
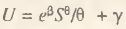 (10)
(10)
Формула (10) позволяет определить группы факторов, от которых зависит субъективная ценность товарной массы. Среди них укажем следующие:
1. Физический объем имеющихся в наличии товарных благ;
2. Ценовые характеристики товарной массы или, более строго, гибкость системы цен. Причем принципиальное значение имеет эластичность цен и по предложению, и по спросу. В свою очередь последние неявным образом зависят от монетарного климата в экономике (от покупательной способности денег).
Что касается закона Госсена, то, как следует из (10), он выполняется, если (1+ѱ)(1–λ)>0. Учитывая, что в нормальных условиях эластичность цен по предложению тяготеет к отрицательным значениям, а эластичность цен по спросу – к положительным, то закон Госсена выполняется практически всегда; вероятность его нарушения пренебрежимо мала и соответствует особо редким случаям, когда экономика претерпевает сверхсложные метаморфозы (например, периоды после кризисного оживления). Определенное своеобразие представляют режимы при θ=0 и θ=1. В этом случае функция полезности уже не зависит от ценовых характеристик производимых благ. Однако полоса возможных конфигураций ценовых характеристик, определяющая искомые режимы, слишком узка. Поэтому если даже в экономике и создастся подобная ситуация, то система не сможет долго находиться в таком состоянии и рано или поздно ’’скатится” в альтернативный режим функционирования. В целом же проведенные модельные построения хорошо иллюстрируют практическую неограниченность производственных и потребительских потребностей общества.
Дополнительный интерес представляют следующие качественные выводы, вытекающие из (10). Во-первых, сдвиги в эластичностях цен по предложению и спросу обладают различной силой влияния на систему общественных предпочтений и оказывают разнонаправленное действие (это следует из формулы 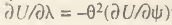 [9]. Во-вторых, в подавляющем большинстве случаев воздействие изменений эластичности цен по предложению значительно слабее, чем при изменении эластичности цен по спросу. Таким образом, ценовые влияния на потребности совокупного потребителя, идущие со стороны реального производства, как правило, оказываются менее значимыми, чем связанные с его ’’внутренними” предпочтениями.
[9]. Во-вторых, в подавляющем большинстве случаев воздействие изменений эластичности цен по предложению значительно слабее, чем при изменении эластичности цен по спросу. Таким образом, ценовые влияния на потребности совокупного потребителя, идущие со стороны реального производства, как правило, оказываются менее значимыми, чем связанные с его ’’внутренними” предпочтениями.
Проведенный достаточно грубый анализ не исчерпывает всех возможностей используемой теоретической схемы (5). Более тонкий учет формальных аспектов может выявить некоторые дополнительные ограничения спросовых возможностей экономических систем.
Мультипликатор Кейнса и ценовые эффекты
Влияние роста цен на поведенческие свойства экономической системы до сих пор остается не до конца ясным. Так, например, с одной стороны, ненулевая инфляция является обязательным атрибутом экономического роста, а, с другой, гиперинфляция приводит к стагнации и сокращению производства. В этой связи представляется, что предложенная модель (5) позволяет продвинуться вперед при изучении данного вопроса.
Для выяснения характера воздействия роста цен на объемы производства будем использовать маржиналистскую концепции' мультипликатора Дж. Кейнса, в соответствии с которой существует связь между увеличением инвестиций и расширением экономической активности, что н статической форме выражается зависимостью: Y=PS=rК, где К – валовые капиталовложения за рассматриваемый период, включающие инвестиции предприятий, домашних хозяйств и государства, а также потребление в секторе администрации и некоторые позиции внешнеторговых связей; r – мультипликатор Кейнса [1]. Если среднюю величину инвестиций, обращающихся в системе, обозначить как N, то К=GN. где G – число оборотов N в течение рассматриваемого периода времени. Подставив модифицированное таким образом кейнсианское выражение PS=rNG в соотношение (5), получим уравнение [10]:
rNG = P2[(πD)/(dU/dS)]. (11)
По-видимому, полученная квадратичная зависимость между объемом инвестиций и уровнем цен является ключом к поставленной проблеме ’’экономический рост – движение цен”. Такой существенно нелинейный тип зависимости означает следующее. Учитывая относительную динамическую стабильность мультипликатора Кейнса и предельной полезности товаров, любое увеличение цен требует резкого возрастания масштабов капиталовложений. Так, например, при неизменности остальных макропараметров (II) двукратный рост цен требует 4-кратного увеличения ’’индуцирующей” порции инвестиции. Понятно, что такой инвестиционный взрыв практически нереален. Частичное положение может выправиться за счет увеличения скорости оборачиваемости капиталовложений. Однако, полностью возникший колоссальный разрыв в спросе на капитал нельзя преодолеть за счет данного фактора, так как скорость оборота ’’старого" капитала имеет естественный предел.
Невозможность столь масштабных вложений капитала и столь быстрой его оборачиваемости приводит к относительному угасанию инвестиционной активности и неизбежно влечет за собой падение производства. Если происшедшие изменения в величинах N и G ’’недотягивают” до полной компенсации роста цен, то происходит снижение эффективного спроса D. девальвация денежных знаков (уменьшение π) и увеличение эффекта мультипликатора. Если рост цен полностью поглощен соответствующей адаптацией мультипликатора r, то, учитывая, что r(1–c)=1, где с – предельная склонность к потреблению, это означает сверхсильную деформацию потребительских ориентаций населения. Так, например, при увеличении цен в 2 раза предельная склонность к потреблению с 20% должна возрасти до 80%. Таким образом, резко сокращается доля накоплений и начинается так называемое бегство от денег. Подобный эффект возможен лишь при устойчиво высокой инфляции, задействующий механизм инфляционных ожиданий. В противном случае переломить сложившиеся потребительские нормы вряд ли удастся. Отметим также, что зависимость (11) хорошо объясняет наблюдаемый факт интенсивной миграции капитала при высоких темпах роста цен в сферы с быстрой окупаемостью вложений – торговлю, посредническую деятельность, финансовые операции и т.п.
Из сказанного ясно, что любое резкое увеличение цен оказывает депрессивное влияние на экономическое развитие по крайней мере в краткосрочном периоде. Восстановить положение без ущерба для макропеременных, входящих в (11), можно только путем резкого скачка в эффективности капиталовложений и снижения предельных издержек производства, а этого нельзя добиться при неизменной технологической базе. Подобные технологические преобразования требуют определенного времени, в течение которого будет наблюдаться процесс стагнации. Аналогичные выводы можно получить при использовании традиционного аппарата производственных функций (для этого объем производства следует представить в виде разложения Эйлера через макрофакторы, которое и подставляется в (5). Таким образом, любой рост цен, с одной стороны, дает импульсы к обновлению производственных фондов и инициирует научно-технический прогресс, а, с другой, служит одним из источников экономических спадов и кризисов. Следовательно, инфляция является тем неизбежным злом, с которым приходится мириться и которое при правильном макрорегулировании можно достаточно успешно использовать в экономических целях.
Общество как кибернетическая система
Маржинальные законы и свойства экономических систем имеют как прикладное, так и философско–идеологическое значение. В этой связи прежде всего хотелось бы отметить чрезвычайно важное значение закона Сэя. В соответствии с ним экономический рост представляет собой спиралеобразный процесс: благодаря действию закона удовлетворения общественных потребностей имеющийся спрос на определенные блага стимулирует рост производства, конечным результатом чего является образование определенной величины совокупного предложения на товарном рынке: далее в соответствии с законом Сэя образовавшееся предложение порождает свой собственный спрос, что стимулирует очередной виток расширения производства. Действие такого механизма позволяет рассматривать экономическую систему как кибернетическую, где в качестве ее подсистем выступают агрегированные спрос и предложение. Возмущающее воздействие со стороны спроса на предложение в этом случае образует канал прямой связи; воздействие предложения на спрос формирует контур обратной связи |7].
Главной особенностью данной системы является положительный характер прямых и обратных связей, то есть имеет место функциональная зависимость типа ’’чем больше, тем больше” (закон Сэя в рассматриваемом случае постулирует положительный характер обратных связей). Однако известно, что наличие положительных прямых и обратных связей, вообще говоря, ведет к саморазрушению системы за счет непрерывного взаимоусиления возмущающих воздействий, которые и генерируют импульсы к ’’саморасшатыванию” и ’’разносу” системы [7]. В случае экономических макрообразований негативное влияние закона Сэя заключается в том, что индуцируемый им постоянный экономический рост, как правило, сопровождается индустриализацией и урбанизацией общества. Кроме того, для квазиравновесных (относительно устойчивых) состояний системы характерен слабый энергетический обмен между системой и окружающей средой при высокой информационной связи между ними [9]. Это означает, что общество должно представлять собой достаточно совершенную информационную систему, в которой отклонения от своего оптимального состояния устраняются путем минимальных финансовых, энергетических, материальных и трудовых затрат. Однако именно этот принцип поддержания гомеостаза в экономических Системах постоянно нарушается (бурение дополнительных скважин для добычи сырья, рост выбросов в окружающую среду, строительство новых электростанций и т.п.). Подобное развитие социально–экономической системы неизбежно приводит к полному отторжению человека от природы, когда само дальнейшее существование человеческих сообществ ставится под вопрос. В данном контексте закон Сэя представляет собой своеобразную экономическую ловушку для общества, отражая его апокалиптическую ’’обреченность” на бесконечный производственный прогресс вплоть до саморазрушения.
Кроме того, процесс неконтролируемого разрастания сферы производственных отношений постепенно приводит к подчиненности человека и природы производственным интересам. В этом случае производство становится самодовлеющим феноменом, формирующим систему ценностей человека как нечто производное от нужд самого производства. В результате человек, по словам Л.Столерю, перестает быть хозяином экономического прогресса, а становится его игрушкой [1]. Такая ситуация означает, что в системе ’’спрос – предложение” кибернетические связи меняются местами: прямая связь становится обратной, а обратная – прямой (в общем случае эту возможность применительно к социальным системам впервые строго рассмотрел Л.А.Петрушенко в [10]).
Другим ’’опасным” следствием разрастания экономической системы является стремительное увеличение ’’холостых” затрат на управление. Это связано с тем, что, с одной стороны, возникновение новых экономических элементов и связей влечет неизбежное усложнение всей производственной (управляемой) системы. С другой стороны, в соответствии с кибернетическим принципом У.Р. Эшби, известного также в качестве закона необходимого разнообразия, степень сложности управляющей системы должна быть не меньше степени сложности управляемого объекта [11].
Таким образом в ’’недрах” социально-экономической системы действуют законы, создающие объективные предпосылки для ее ’’смерти”. При этом экономическая смерть системы отнюдь не означает ее физического разрушения. В данном случае происходит возрастание энтропии в экономической системе и потеря ее управляемости.
В связи с вышесказанным проанализированные маржинальные свойства экономических систем имеют значение с точки зрения понимания тех условий, которые необходимы для нейтрализации (ослабления) закона Сэя во избежание экономического ’’перегрева”. Некоторые из таких условий возникают спонтанно, другие могут целенаправленно создаваться. При этом важен следующий факт: если нарушается закон Сэя, то автоматически нарушается и закон удовлетворения общественных потребностей и наоборот. Это означает, что если система ’’спрос – предложение” попадает в подобное состояние, то в ней одновременно ’’рвутся” и прямые, и обратные положительные связи. Таким образом, кибернетический цикл ’’спрос – предложение” всегда имеет либо строго положительный, либо строго отрицательный характер.
Практическое использование закона Cэя
В определенных случаях маржинальные законы и свойства можно использовать при разработке более основательных макроэкономических регулирующих воздействий с учетом того режима, в котором функционирует экономическая система. Теоретически закон Сэя является одним из проявлений мультипликативных эффектов в экономике. Данный факт в значительной мере предопределяет характер управления экономическими процессами.
Типичным примером использования закона Сэя является учет его действия при разработке мер антициклической и антиинфляционной политики. В частности, существование закона Сэя ’’перечеркивает” доктрину роста производства в качестве антиинфляционного рычага при повышении цен. Представления, лежащие в основе такого подхода, основаны на желании восстановить материально–финансовую сбалансированность экономики путем наращивания объемов товарной массы. Однако в соответствии с законом Сэя выпуск товаров, по стоимости равный величине имеющегося дефицита, означает выплату соответствующей заработной платы по всей цепочке межотраслевых связей. В результате сумма полученных доходов будет равна стоимости выпущенных товаров и прежняя несбалансированность рынка сохранится в прежнем размере. В связи с этим макроэкономическая политика, направленная на рост выпуска товаров и услуг, может улучшить экономическое положение только в том случае, если она ставит цель увеличить емкость рынка путем прогрессивной структурной перестройки экономики и перепрофилирования производств, работающих на поддержание собственной деятельности в рамках замкнутых воспроизводственных циклов. Для практической разработки макрополитики удобно использовать межотраслевые схемы (модель ’’затраты – выпуск” В.Леонтьева). В частности, в балансовой матрице прямых затрат нулевые элементы соответствуют отсутствию межотраслевых поставок. В некоторых случаях наличие таких элементов позволяет разбить систему на подгруппы отраслей, производство в которых может осуществляться более или менее автономно. Данный принцип лежит в основе концепции разложимости матрицы прямых затрат, в соответствии с которой экономическая система может распадаться на несколько кластеров отраслей, каждая из которых работает в режиме полного самообеспечения, при отсутствии взаимодействия между ними. Именно наличие подобных ’’узких мест” в экономике и является основным фактором, порождающим инфляцию. Смысл же антиинфляционных мер должен заключаться в том, чтобы разрушить возникшую в народном хозяйстве технологическую автономность соответствующих отраслей и ’’вывести” их на консолидированный потребительский рынок.
Литература
[1] Л. С т о л е р ю. Равновесие и экономический рост. М., 1974.
[2] Л. Харрис. Денежная теория. М., 1990.
[3] И.В. Филаточев. Концепции ’’открытой экономики”: интернационализация и макроэкономическая политика государства. М., 1991.
[4] М. И н т р и л и г а т о р. Математические методы оптимизации и экономическая теория. М., 1975.
[5] М. В е й ц м а н. Модель синдрома дефицита (’’Экономика и математические методы”, 1990, Т. 26. Вып. 6).
[6] Дж. Хикс. Стоимость и капитал. М., 1988.
[7] Л. А. Петрушенко. Принцип обратной связи. М., 1967.
[8] А. Маршалл. Принципы экономической науки. М., Т. 3, 1993.
[9] Н. Вине р. Кибернетика. М.. 1983.
[10] Л. А. Петрушенко. К вопросу о социальном моделировании. (’’Известия ЛЭТИ”, 1963. Вып. 48).
[11] У.P. Эшби. Введение в кибернетику. М., 1959.
[1] Здесь и далее в квадратных скобках ссылки на литературу.
[2] Понятно, что при учете фактора временной синхронизации экономических сделок догма Смита теряет свой содержательный смысл.
[3] Заметим, что уравнение (1) описывает движение стоимостных показателей. Если ввести в рассмотрение ценовой фактор и понятие эластичности цен по предложению товаров 1=(S/P)(∂P/∂S), то для натуральных объемов спроса и предложения оно примет вид:
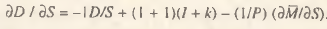
Отсюда следует вывод: при абсолютном росте цен действие закона Сэя усиливается.
[4] Похожие модельные построения имеются у М. Вейцмана, который исследует связь искажений в стоимостях товаров со степенью их дефицитности [5]. Однако в отличие от М. Вейцмана мы рассматриваем относительные искажения цен на макроуровне, а не их абсолютные деформации применительно к микропоказателям.
[5] Более строго π представляет собой предельную полезность денег и может восприниматься в качестве ценового дефлятора. С учетом того, что F=F(M) – функция полезности денег, модель (5) можно представить в следующей эквивалентной форме:
Р(D/S) = (dU/dS)/(dF/dM).
[6] В дальнейшем будет показано, что вытекающее из (5) тождественное определение агрегатной функции полезности для непрерывного и дискретного случаев соответственно (для простоты будем полагать π = 1).

с аналитической точки зрения является более "бедным’', чем уравнения (7), (8) и (9). Тем не менее, приведенные формулы имеют важное значение, так как из них следует достаточно прозрачное представление о макроэкономической полезности товарной массы, а именно: функция полезности есть сумма относительных величин избыточного спроса на всех товарных рынках, взвешенных по цепам. В случае равновесия на рассматриваемых рынках функция полезности представляет собой сумму цен (стоимостей) всех рассматриваемых благ. Таким образом, (5) позволяет агрегировать микроэкономические эффекты.
[8] Указанный факт имеющегося различия в форме кривой U(S) в зависимости от выполнения закона Сэя автоматически следует из анализа стационарных точек функции полезности. Для общего случая точка максимума определяется следующий образом (β – константа)
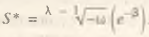
При λ = 0 данный оптимум стягивается в точку 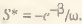
[9] Из приведенной формулы вытекает также, что dѱ/dλ = θ2, то есть возрастание эластичности цен по спросу сопровождается ростом эластичности цен по предложению. Таким образом, любое повышение чувствительности цен связано с совершенствованием всего ценового механизма.
[10] Соотношение PS=rNG позволяет выяснить также связь между мультипликатором Кейнса и законом Сэя:
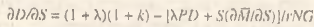
Отсюда видно, что взаимосвязь закона Сэя и мультипликатора Кейнса в общем случае не однозначна и зависит от выражения в квадратных скобках.
Официальная ссылка на статью:
Балацкий Е.В. Маржинальные свойства экономических систем// «Мировая экономика и международные отношения», №7, 1995. С.123–137.