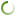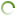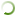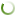Зона фискальный противоречий (з.ф.п.) (area of fiscal contradictions) – это символическое расстояние между точками Лаффера 1-го и 2-го рода.

В 2003 г. Е.В.Балацким (E.V.Balatsky) была высказана идея о том, что кривой Лаффера налоговой (fiscal Laffer curve), которая описывает зависимость объема налоговых поступлений от налогового бремени, не достаточно для понимания результативности фискальной (налоговой) политики. Для более глубокого анализа необходимо рассмотрение еще одной кривой – производственной кривой Лаффера (production Laffer curve), описывающей зависимость объема производства (ВВП) от налогового бремени. Совместное рассмотрение двух кривых позволяет по-новому посмотреть на эффективность фискальной политики.

Производственная кривая Лаффера описывается зависимостью Y=Y(q) в системе координат «налоговое бремя (q) – объем производства (Y)», где Y – объем ВВП страны, q – фактическая фискальная нагрузка (q=T/Y). Тогда кривая Лаффера налоговая описывается зависимостью T=T(q) в координатной плоскости «налоговое бремя (q) – объем налоговых платежей (T)». При этом постулируется два важных обстоятельства. Первое состоит в том, что производственная кривая Лаффера имеет локальный максимум в точке q*, которая называется точкой Лаффера 1-го рода и удовлетворяет следующим условиям: dY(q*)/dq=0; d²Y(q*)/dq²<0. Второе обстоятельство состоит в том, что кривая Лаффера налоговая также имеет локальный максимум в точке q**, получившей название точки Лаффера 2-го рода и удовлетворяющей условиям: dT(q**)/dq=0; d²T(q**)/dq²<0.

Так как справедливо соотношение T=qY(q), то считается, что производственная кривая Лаффера выступает в качестве «первичной» аналитической конструкции, тогда как кривая Лаффера налоговая оказывается «вторичной» в том смысле, что она автоматически получается из производственной зависимости путем ее умножения на налоговое бремя. Кроме того, из зависимости T=qY(q) видно, что объем налоговых поступлений испытывает двойное влияние со стороны величины налогового бремени. Такая форма двух кривых обеспечивает важное свойство, а именно: q*<q**, т.е. точка Лаффера 2-го рода всегда больше точки Лаффера 1-го рода. Данное обстоятельство позволяет ввести в рассмотрение показатель расстояния между точками Лаффера 1-го и 2-го рода: Δq=q**–q*. Схематично данный эффект показан на рис.1.

Величина фискального «разрыва» Δq очерчивает некую полосу (обозначена штриховкой на рис.1), которая называется з.ф.п. и обладает важными свойствами. В з.ф.п. имеет место фискальный антагонизм: рост налогового бремени «полезен» бюджету и, следовательно, государству, но крайне «вреден» производителю, т.е. интересы одного экономического агента достигаются за счет ущемления интересов другого агента. Это автоматически вытекает из того факта, что в з.ф.п. участвует нисходящая ветвь производственной кривой Лаффера и восходящая ветвь кривой Лаффера налоговой. Таким образом, з.ф.п. – это зона значений налогового бремени, в которой интересы производителя и государства оказываются в противоречии.

Введение в рассмотрение з.ф.п. несет в себе новое понимание эффективности фискальной политики: чем больше ширина этой зоны, тем больше антагонизм между стимулирующей и фискальной функциями налоговой системы страны и тем меньше шансов устранить этот антагонизм. И, наоборот, узкая з.ф.п. означает, что интересы производителя и государства почти синхронизированы: что плохо (хорошо) для предпринимателя, то плохо (хорошо) для бюджета и государства. Тем самым при макроэкономическом оценивании величина Δq дает количественную характеристику того, насколько хорошо настроена фискальная система государства под интересы производителей, от активности которых зависит налоговая база.

Эконометрические расчеты, выполненные в 2004 г., показали, что для экономики США за период 1986–2000 гг. средняя величина з.ф.п. составляла 1 процентный пункт (п.п.), тогда как для экономики России 1989–2000 гг. она составляла 6 п.п. Данный факт показал низкую эффективность российской фискальной системы и раскрыл глубинные проблемы ее формирования в переходный период.

В более поздние годы з.ф.п. подвергалась переосмыслению и различным интерпретациям. Так, в 2010 г. проф. И.А.Майбуров интерпретировал з.ф.п. как разновидность налоговой ловушки. В частности, фискальная политика, при которой налоговое бремя выше точки Лаффера 2-го рода (q>q**), классифицируется как основная налоговая ловушка, а политика, при которой налоговое бремя находится внутри з.ф.п. (q*<q<q**), трактуется как дополнительная налоговая ловушка.

Интерпретации и объяснения 2004 г. феномена з.ф.п. делают акцент на его двойственной природе. С одной стороны, наличие широкой з.ф.п. свидетельствует о плохой конфигурации фискальной системы, с другой стороны, это говорит о заторможенной реакции производителя. Причинами последней могут быть отсутствие альтернативных сфер инвестирования, территориальная иммобильность производства, специфическая психология производителя и т.п.

Практика эконометрической оценки з.ф.п. вскрыла множество вычислительных проблем. Так, построение производственной кривой для переменной ВВП в абсолютных значениях оказывается очень трудоемким и зачастую дает неудовлетворительные результаты, тогда как использование переменной темпа роста ВВП позволяет получить гораздо лучшие результаты. Однако в этом случае усложняется процедура расчета точек Лаффера 1-го и 2-го рода. Процесс совершенствования методов идентификации з.ф.п. продолжается.

Понятие з.ф.п. в модифицированном виде может быть использовано и при изучении кривой Арми–Рана, которая описывает похожие процессы, но не в сфере доходов бюджета, а в сфере бюджетных расходов. Учитывая действие закона Вагнера, можно говорить, что со временем з.ф.п. немного смещается вправо по оси абсцисс, что отражает эволюционную природу данного явления.

Понятие з.ф.п. имеет ограниченное распространение; в основном оно находит применение в аналитической практике экономистов России, Украины и Грузии. Такое положение дел во многом связано с наличием критики в адрес концепции кривой Лаффера, лежащей в основе понятия з.ф.п. Помимо традиционных теоретических контраргументов против концепции з.ф.п. наиболее важными являются следующие критические положения:

- большинство расчетов показывает, что фактическое налоговое бремя для всех стран находится, как правило, внутри з.ф.п., что свидетельствует о почти полной невозможности воплотить принципы з.ф.п. в практику налогового регулирования;

- использование в концепции з.ф.п. понятия среднего налогового бремени не позволяет напрямую понять, за счет каких налоговых ставок нужно уменьшать совокупное налоговое бремя; для ответа на данный вопрос необходимы дополнительные прикладные расчеты, которые сами по себе представляют нетривиальную вычислительную процедуру.

Наличие таких методических проблем ведет к тому, что применение на практике концепции к.л.н. требует тщательной подготовки первичных статистических данных и предельно корректной интерпретации получаемых результатов.

Литература

1. Балацкий Е.В. Анализ влияния налоговой нагрузки на экономический рост с помощью производственно-институциональных функций// «Проблемы прогнозирования», №2, 2003. С.88–107.

2. Балацкий Е.В. О природе несостоятельности российской фискальной системы// «Общество и экономика», №11–12, 2004. С.127–136.

3. Налоговая политика. Теория и практика: учебник для магистрантов, обучающихся по специальностям «Финансы и кредит», «Бухгалтерский учет, анализ и аудит», «Мировая экономика»/ Под ред. И.А.Майбурова. М.: ЮНИТИ-ДАНА, 2010. 519 с.

Официальная ссылка на статью:

Балацкий Е.В. Зона фискальных противоречий/ Энциклопедия теоретических основ налогообложения/ Под ред. И.А.Майбурова, Ю.Б.Иванова. М.: ЮНИТИ-ДАНА, 2016. С.61–64.