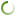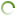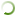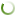Кривая Арми–Рана (к.а.р.) (Armey–Rahn curve) – это гипотетическая кривая параболической формы с характерной для нее точкой максимума, которая связывает экономический рост страны с долей государственных расходов в ВВП.

Считается, что в работах Р.Барро (R.Barro) 1993 г., Р.Арми (R.Armey) 1995 г., Р.Рана (R.Rahn) 1996 г. и Дж.Скалли (G.Scully) 1998 г. были заложены теоретические и эмпирические основы теории оптимального размера правительства. Именно работы этих авторов 1993–1998 гг. способствовали популяризации данной концепции. Иногда горбообразную функцию, связывающую темпы экономического роста с долей государственных расходов в ВВП, называют обобщенно BARS-кривой по начальным буквам ее популяризаторов (Barro, Armey, Rahn, Scully). Иногда данную зависимость называют просто кривой Рана, кривой Арми или к.а.р. Учитывая, что именно Ричард Арми (Richard Armey) и Ричард Ран (Richard Rahn) внесли наибольший вклад в популяризацию указанной кривой и в ее превращение в рабочий инструмент современного экономического анализа, она чаще всего называется к.а.р., а ее возникновение датируется 1995–1996 гг.

В соответствии с принятой традицией размер государства измеряется долей государственных расходов в ВВП: g=G/X, где X – объем валового внутреннего продукта (ВВП), G – величина государственных расходов. Тогда зависимость темпов экономического роста страны (λ=ΔX/X) от размера государства (g) описывается параболической функцией с характерной для нее точкой максимума. Такая зависимость называется к.а.р. и графически представлена на рис.1. Иногда параболическую зависимость между абсолютным размером ВВП и долей государственных расходов также называют к.а.р.

Неотъемлемым элементом к.а.р. является ее точка максимума, которая в литературе получила название точки Скалли по имени Джеральда Скалли (Gerald Scully), много лет изучавшего влияние бюджетной политики на экономический рост и оценившего точку максимума на кривой к.а.р. в 23% для экономики США. Впоследствии данная величина много раз пересматривалась, но за точкой максимума к.а.р. закрепилось название точки Скалли (g*), для которой выполняются условия: ∂λ/∂g=0 и ∂²λ/∂g²<0. В 2011 г. такая точка получила название динамической точки Скалли, подчеркивая тот факт, что данная точка максимизирует темпы роста ВВП, а не саму величину ВВП; превышение данной величины означает падение темпов роста ВВП, но не самого ВВП. Для оценки уровня доли государственных расходов, превышение которой грозит падением абсолютной величины ВВП, служит статическая точки Скалли (g**), которая находится при условии λ=0. При этом имеет место условие: g*<g**. Превышение величины g** вводит национальную экономику в режим рецессии. Тем самым динамическая точка Скалли показывает желательное значение регулятора g, а статическая точка Скалли – тот предел увеличения размера государства, за который заходить категорически не рекомендуется.

Эконометрические расчеты позволили определить значения точек g* и g** для разных стран. При этом оказалось, что величина статических точек Скалли в среднем на 5–6 п.п. больше значений динамических точек Скалли. Данный интервал показывает диапазон государственного регулирования, который отделяет политику достижения максимальных темпов экономического роста от режима рецессии.

В развернувшейся дискуссии относительно оптимальных размеров государства экономист Дэниэл Митчелл (Daniel Mitchell) обратил внимание на интересный факт, показывающий значение кривой Арми–Рана и точек Скалли. В 2003 году в США параметр g составлял 35,7% против 47,6% в ЕС-15. Почти 12-процентный разрыв сопровождался следующей картиной: душевой ВВП США в этом же году был на 40% выше, чем в ЕС-15 (37,6 против 26,6 тыс. долл.), а средний темп роста ВВП за период 1993–2003 гг. был на 50% выше (3,2 против 2,1%). Данный пример дает основания полагать, что избыточные государственные расходы в странах Европы делают их менее динамичными и менее богатыми по сравнению с США. Дискуссии по данному вопросу продолжаются.

В экономической теории к.а.р. тесно связана с законом Вагнера и выступает в качестве его естественного ограничителя. Если закон Вагнера постулирует повышательное влияние ВВП на долю государственных расходов в ВВП и устанавливает тем самым прямую связь в подсистемах «экономика–государство», то к.а.р. фиксирует обратную связь между ними. Причем эта обратная связь оказывается неоднозначной: на определенных этапах развития рост доли госрасходов в ВВП ведет к ускорению роста ВВП, а иногда – к его торможению. Логика взаимодействия двух подсистем может быть схематично представлена в виде кибернетического контура на рис.3. Тем самым наличие к.а.р. превращает подсистемы «экономика» и «государство» в саморегулирующуюся рыночную систему, в которой однонаправленное развитие событий периодически корректируется отрицательной обратной связью в виде нисходящей ветви к.а.р.

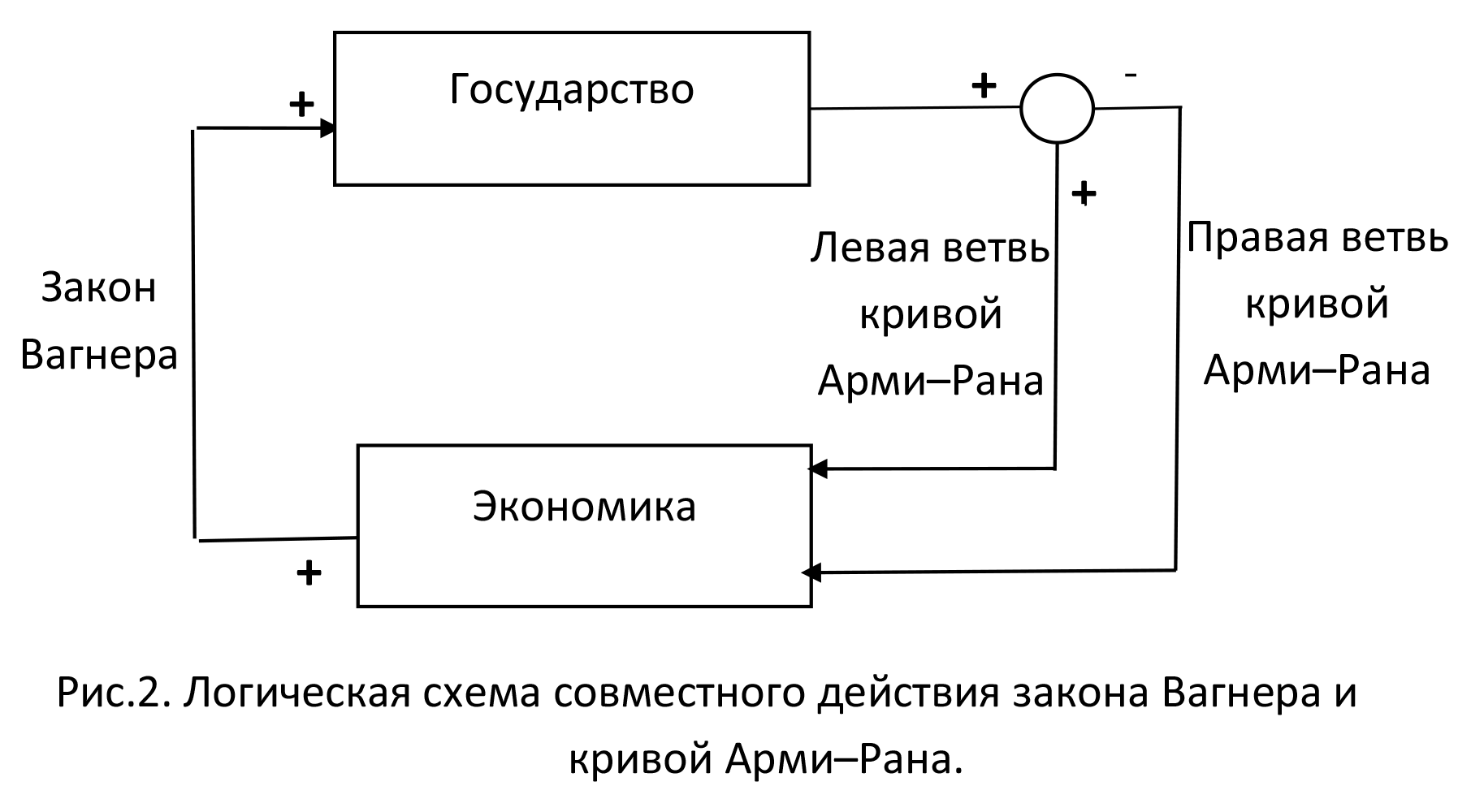
Объединение закона Вагнера и к.а.р. в рамках единой аналитической конструкции дает интересный результат, известный как парадокс богатства, в соответствии с которым рост ВВП ограничивает свой собственный рост. Данный парадокс вытекает из формулы кривой, описывающей закон Вагнера: _, где m и θ – параметры, причем m>0, а θ>1. Тогда доля государственных расходов в ВВП (g=G/X) описывается выражением: _. В силу закона Вагнера данная функция является возрастающей, однако в соответствии с к.а.р. это возрастание будет плодотворным пока доля государственных расходов в ВВП не превысит динамическую точку Скалли (g*); при g>g* темпы роста ВВП уменьшаются. Этой точке соответствует величина ВВП Х*:

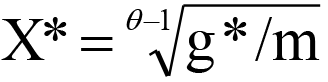                                                                                               ₍₁₎  

Если рост доли государственных расходов в ВВП превысит и статическую точку Скалли (g>g**), то экономический рост сменится рецессией. Этой точке соответствует величина ВВП Х**:

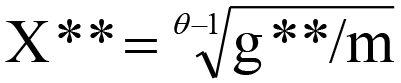                                                                                           ₍₂₎

Парадокс богатства имеет смысл только при выполнении закона Вагнера, т.е. когда θ>1. Таким образом, закон Вагнера выступает ограничителем долгосрочного роста экономики. Преодолевается парадокс богатства путем нарушения или инверсии закона Вагнера и переходом к политике более умеренных государственных расходов. Именно этот эффект фиксируют эконометрические тесты закона Вагнера, показывающие перестройку режима экономического развития в богатых странах, когда эластичность государственных расходов уменьшается с θ>1 на θ<1. Тем самым парадокс богатства объясняет ступенчатый характер вытеснения закона Вагнера из мировой экономики: сначала он нарушается в самых богатых странах с большим ВВП, еще через какое-то время в странах, выходящих на необходимый уровень богатства, и т.д. Иногда в модельных построениях вместо величины ВВП (Х) используется показатель душевого ВВП, что делает все выводы еще более выпуклыми и лучше интерпретируемыми: закон Вагнера нарушается в странах с высоким уровнем благосостояния, т.е. с большим душевым ВВП.

Теоретически к.а.р. имеет свой аналог применительно к государственным доходам – производственную кривую Лаффера. Обе кривые имеют различные модификации, но для всех характерна параболическая форма с точками максимума. Эти две кривые описывают две стороны бюджетной политики: политику доходов (налогов) – кривая Лаффера, политика расходов – к.а.р. При этом можно говорить, что налоговая политика выступает в качестве первичного элемента бюджетной политики, а политика расходов – вторичного. Следовательно, кривая Лаффера выступает в качестве первичного звена макроэкономического анализа по сравнению с к.а.р. Это связано с тем, что процесс изымания доходов предшествует процессу государственных расходов.

Учитывая органическую связь между к.а.р. и кривой Лаффера, легко проследить и аналогию между точкой Скалли и точкой Лаффера, которые фиксируют перегибы на соответствующих нелинейных кривых. Сопряжение двух кривых и характерных для них критических точек позволяет объединить важные нюансы политики налоговой и политики государственных расходов в рамках единой макроэкономической политики.

Концепция к.а.р. до сих пор не получила всеобщего признания. В ее адрес высказывается множество критических аргументов, которые во многом сходны с замечаниями в адрес кривой Лаффера. Наиболее важными среди них являются следующие:

- показатель доли государственных расходов в ВВП не является простым и однозначным; иногда оценивается только масса расходов федерального правительства, иногда – суммарные расходы государства, включая расходы региональных и муниципальных властей. Такие разночтения приводят к смещению всех количественных оценок и содержательных выводов;

- рост государственных расходов часто сопряжен с ростом бюджетного дефицита, который в свою очередь ведет к росту ставки рефинансирования и охлаждению деловой активности; это так называемый контраргумент «ястребов дефицита», требующий строгого ограничения роста государственных расходов;

- показатель доли государственных расходов в ВВП не учитывает структуру производимых бюджетных затрат. Между тем различные статьи бюджетных выплат имеют совершенно разную эффективность как в смысле отдачи государственных вложений, так и в смысле стимулирующего (мультипликативного) эффекта на экономику.

Обозначенные проблемы ведут к тому, что применение на практике концепции к.а.р. довольно ограничено, а все количественные оценки подвергаются очень осторожной экономической интерпретации.

Литература

1. Балацкий Е.В. Закон Вагнера, кривая Арми–Рана и парадокс богатства// «Общество и экономика», №9, 2010. С.80–97.

2. Балацкий Е.В., Екимова Н.А. Налогово-бюджетная политика и экономический рост// «Общество и экономика», №4-5, 2011. С.197–214.

3. Armey D. The Freedom Revolution. Washington: Regnery Publishing Co, 1995. 318 p.

4. Barro R. A Cross-Country Study of Growth, Saving and Government// «NBER Working Paper», 1989. No.2855. 55 p.

5. Mitchell D. The Impact of Government Spending on Economic Growth// «Backgrounder», No.1831, March 31, 2005. Heritage Foundation. 18 p.

6. Rahn R., Fox H. What Is the Optimum Size of Government. Denver: Vernon K. Krieble Foundation. 1996.

7. Scully G. Measuring the Burden of High Taxes// «Policy Report», No.215. Dallas: National Center for Policy Analysis. 1998. 16 p.

Официальная ссылка на статью:

Балацкий Е.В. Кривая Арми–Рана/ Энциклопедия теоретических основ налогообложения/ Под ред. И.А.Майбурова, Ю.Б.Иванова. М.: ЮНИТИ-ДАНА, 2016. С.108–111.