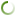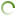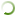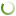Market fluctuations adversely affect any economy which experiences a shrinkage of effective demand. This process leads to the underutilization of national resources, which remain unclaimed. At the macroeconomic level, this manifests itself, as a rule, in the growth of unemployment and a decline in the rate of utilization of production capacities. In an economic crisis, the oversupply of national resources reaches staggering dimensions, and the production system is functioning at almost half its capacity. This state of affairs calls for appropriate managerial action. Which indicates the need to estimate the nation’s macroeconomic potential in order to ascertain economic losses on a nationwide scale. What is called the index of potential gross domestic product (GDP) is commonly used for these purposes. However, the methods of its calculation are ambiguous, if not controversial. Therefore, let us consider the main approaches available in this area and possible alternative algorithms for estimating potential GDP.

Conventional econometric methods of estimating potential GDP

Econometric techniques are applied in most cases to the estimation of potential GDP. Two alternative approaches can be distinguished, which may be regarded as rival in a way. Let us consider them in greater detail.

The "labor” method is based on the formulation of a macroeconomic, as a rule, two–factor production function by drawing on such traditional macroparameters as labor and capital. In this case, the production function takes this form (to make our analysis more illustrative and concrete, we use here the Cobb–Douglas production function as specified by I. Tinbergen):

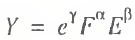                                                                                          (1)

where Y is actual GDP; t is time; F is the volume of fixed capital; E is the number employed in the economy; α, β, and γ are parameters estimated on the basis of retrospective statistical arrays. (The indices Y and F are reckoned in comparable prices.)

Considering that L is the labor force and U is the number of unemployed (L = E+ U), Eq. (1) may be represented in this form:

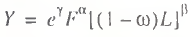                                                                               (2)

where ω = U/L is the actual rate of unemployment.

According to the “labor” method, manpower is an underutilized factor [1]. Therefore, the unemployment rate amounts to a flat deduction from the potential GDP, since its engagement in economic turnover is equivalent to the formation of an extra portion of value added. Recognizing that every economy has a certain ‘natural’ rate of unemployment ω*, the potential GDP Y* is calculated by the following formula:

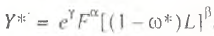                                                                          (3)

From Eqs. (2) and (3), it is easy to derive a formula for a kind of “efficiency coefficient” of the economy, which is the ratio of actual to potential GDP Y/Y* (this index is defined in [2] as the productive potential utilization rate), i.e.,

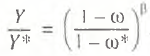                                                                                       (4)

As it can be seen from Eq. (4), the rate of underproduction Y/Y* depends on the rate of labor underutilization and elasticity β, showing labor endowment, as a macrofactor, to production output. Clearly, rate of underproduction cannot be calculated without preliminary econometric estimates of the production function (1).

By using formula (2), it is possible to derive another major characteristic of missed opportunities, namely, the k coefficient showing the percentage ratio in the growth of GDP given 1% decrease in the unemployment rate. It takes this form:

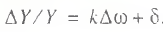                                                                                     (5)

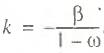                                                                                                (6)

The index δ in formula (5) accumulates the effect produced by all other changes.

For the simplest linearly homogeneous production function, formula (6) is specified as follows:

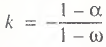                                                                          (7)

From Eqs. (6) and (7), we arrive at a very interesting conclusion: the closer an economy is to full employment, the less the production effect is from a decrease in unemployment rates.

The “capital” method is offered in [2]. It also involves the modeling of a production function. However, the calculation method here is somewhat altered, and the initial functional relation takes the form

                                                                                                      (8)

where К is the volume of operational production capacities.

According to this method, the econometric estimation of output should be preceded by the recalculation of capital stocks, proceeding from the actual utilization rate of production capacities. Considering that 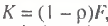, where ρ is the rate of underutilization of capital stocks, formula (8) may be represented as follows:

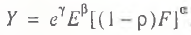                                                                                       (9)

The “capital” approach assumes that economic losses are incurred primarily by the inefficient utilization of production capacities. Therefore, the volume of idle production equipment can be treated as a flat deduction from the nation’s potential GDP, since its withdrawal would increase the output of final products. Assuming that an economy always has a certain amount of reserve capacities characterized by the rate of ‘natural’ underutilization, ρ*, potential GDP can be calculated by this formula:

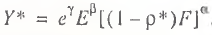                                                                                  (10)

Then, on the basis of Eqs, (9) and (10), the rate of underproduction is computed as

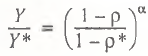                                                                                               (11)

The coefficient m, showing the percentage ratio in the growth of GDP given 1% decrease in the underutilization rate of production capacities, is calculated similarly to (6):

                                                                                                      (12)

The same principle of decreasing efficiency underlies the utilization of resources, namely: the closer an economy is to the full utilization of production capacities, the smaller the production effect is from the increase in their utilization.

Shortcomings of the “labor” and “capital” methods

Both procedures can be classified as one–factor methods for estimating potential GDP, which is evident from their wording. The difference lies only in the choice of macrofactors. The choice of the labor factor has its own logic and historical underpinnings.

For example, the labor method is used in developed countries where labor is, firstly, recognized as a key national resource, secondly, quite costly and burdensome during recession periods, and thirdly, highly responsive to any disturbances in the economy. The above considerations predetermine the fact that the rate of unemployment is treated as a prime indicator of the economic situation, while unemployment statistics reflect quite accurately the real state of affairs.

The capital method was developed to be applied to the Russian economy in transition, when the use of the labor procedure was excluded for several reasons. First, the downswing in production was attended in the Russian economy by a disproportionately slack release of labor. In these conditions, the orientation to the unemployment rate could distort the actual scope of underproduction. On the contrary, the production capacities utilization rate made it possible to assess quite accurately the real depth of economic recession. Second, the unemployment statistics were and still are inadequate. The result in two alternative parameters markedly varying in quantitative terms, each showing a weak correlation with the real state of affairs. Third, unemployment was a new phenomenon for Russia in the 1990s, while the available statistical arrays were too short for a comparative study of potential GDP over long periods.

Each of the two methods has its merits and demerits. For example, the labor approach is essentially macroeconomic and its application at the sectoral level is impossible. The capital method, in contrast, takes into account the level of capital idleness in various segments of the economy, yet the macroeconomic averaging of sectoral data presupposes their weighting. This may lead to serious computation errors. In most cases, the aggregate underutilization of production capacities cannot be accurately estimated, which explains the transference of capital utilization rates in industry onto the entire national economy.

Furthermore, the two methods have common shortcomings.

First, as they rely on two–factor production functions, both methods are essentially one–factor ones. Potential GDP is estimated from the possible lull utilization of only one of the macroresources, although both factors can be used; hence the method used must take it into account. The aforesaid makes it apparent that under the incomplete utilization of two factors, which is the case in reality, both procedures lead inevitably to the underestimation of potential GDP.

Second, one–factor methods imply that one macroresource can be increased while the other remains unchanged. Yet, this is not indubitable. For example, if capital assets are operating at full capacity, additional labor cannot be hired for lack of workplaces. Conversely, under full employment, an increase in the utilization of production capacities will yield nothing, since there is no labor to operate them. In other cases, the situation is similar owing to the fact that the initial balance in production factors has to be maintained. Therefore, methods of calculation of potential GDP should take into account the need for proportional growth of both macrofactors.

In our opinion, the above shortcomings can be easily eliminated by “merging” two traditional one–factor procedures into a single two–factor one.

General algorithm of econometric estimation of potential GDP

Considering the above critical comments on labor and capital estimating procedures, the general algorithm of potential GDP estimation involves two different approaches.

The initial econometric dependence is based on the production function (8), i.e., the calculation base coincides here with the one used in the capital procedure. However, further work with (8) presupposes two alternative procedures.

Thus, the first (asynchronous) method is based on recalculating the actual GDP into the potential one, provided both macrofactors are brought to the level of their ‘natural’ full utilization. In this case, assuming a priori a high elasticity of the macroresources, the sought–for formula takes the form

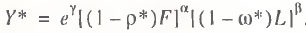                         (13)

Hence, under ω* = ω, the general two–factor method (13) turns into the capital procedure, whereas under ρ* = 0, it turns into the labor procedure. It follows that these two calculation methods are asymmetrical; therefore, a comparison of quantitative estimates obtained on their basis is rather problematic.

The second (synchronous) method involves calculation of potential GDP, based on the balanced full utilization of both macrofactors. In this case, it is assumed that the macroresources lack elasticity and the final formula is of the form:

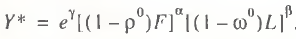                    (14)

where the utilization rates ρ^o and ω^o are calculated by the following rules:

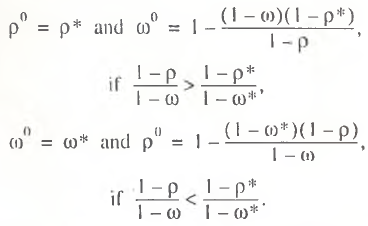
(15)

This approach assumes that GDP cannot be increased by an autonomous increase in one of its resources. It is postulated that both resources should grow simultaneously, keeping unchanged the initial capital–labor ratio KIE, i.e., the correlation between the two macrofactors. Indeed, the balance between labor and capital, which was fixed at one point in time, may be regarded as stationary, and any deviation from it means real readjustment of the national resource potential, entailing certain pressure on the economy. Although this case is not excluded in practice (as specified in formula (13), the synchronous method seems more correct in theory.

It should be pointed out that the synchronous method assumes that the full utilization of one resource is attended, as a rule, by the underutilization of the other resource. In other words, one of the macrofactors proves to be in excess, even under the most favorable market conditions, and this surplus can no longer enlarge the GDP. Therefore, the second method, by its side results, enables us to answer the question as to which macrofactor is potentially more limited. In our view, this aspect of the synchronous method is of particular interest, since it actually provides additional opportunities for the diagnosis of capital overaccumulation and, eventually, for the study of economic cycles themselves.

It follows from (8), (13) and (14) that the production capacity under utilization rate is estimated by the synchronous and asynchronous methods from the following formulas:

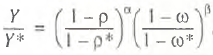                                                                                  (16)

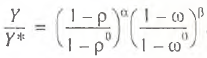                                                                                   (17)

A comparison of (16) and (17) with (4) and (11) reveals the general character of techniques used in the first and second methods. Presently, the proposed general econometric approaches to potential GDP estimation are tenable theoretically and quite reliable in practical use. For example, by applying them to the Russian economy, we have already accumulated a database providing for more or less accurate estimates by formulas (16) and (17).

Alternative methods for estimating potential GDP

Although econometric methods for potential GDP estimation are generally recognized, their wide use in practice is hardly justifiable. In our opinion, it is much more fruitful to use determinist methods based on designing the most primitive and obvious production functions. The choice of such approaches can be as wide as one likes, but here we shall evaluate only two procedures that seem to be the most acceptable for traditional macroeconomic calculations.

The first (linear) method is based on the use of a linear production function.

Considering that actual GDP can be represented by the following equality expressions:

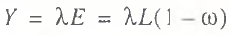                                                                               (18)

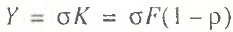                                                                              (19)

where λ is mean labor efficiency and δ is mean capital productivity of operating capacities, the sough–for production function takes the following configuration (formula (20) is obtained by summing (18) and (19) and dividing the total by two):

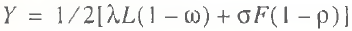          (20)

Dependence (20) is more preferable than the equality expressions (18) and (19), since it accumulates both macrofactors, whose full utilization heightens the production effect. It should be pointed out that a similar production function can be developed by econometric techniques. In this case, however, the function displays constant parameters of labor and capital productivity throughout the entire research interval, whereas dependence (20) involves the variable rates of their efficiency. Potential GDP for production function (20) is estimated by the following formula:

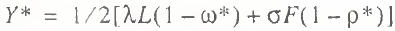                                              (21)

Here, as in the above case, it is possible to use more complicated calculations, where shifts in unemployment and capital underutilization rates are balanced according to the hypothesis that the capital–labor ratio is constant: K/E = const. Nevertheless, as this case does not involve the use of any special techniques, we shall not discuss it any longer here.

Formula (20) provides for the following specification of the k and m coefficients:

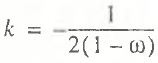                                                                                             (22)

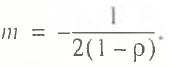                                                                            (23)

A comparison of (22) and (23) with (6) and (12) reveals their similarity, except for the, sole difference that econometric methods assume an unequal redistribution of the effect produced by two macrofactors. This manifests itself most graphically in the structure of linear homogeneous production functions, wherein α + β = 1. In case the statistical estimation of relevant parameters results in α = β, the two–factor econometric and linear determinist methods yield identical values of the coefficients k and m.

As for the utilization rate of productive potential, this is estimated by the formula

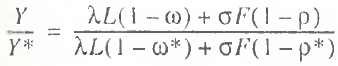                                                         (24)

Of course, the use of (24) presupposes generalization wherever the number of analyzed macroresources exceeds two factors.

The second (quadratic) method is based on the use of a power production function derived by the multiplication of (18) by (19) with the subsequent extraction of the root, i.e.,

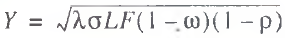                                                                    (25)

Therefore, potential GDP equals

                                                     (26)

In this case, the rate of underproduction is calculated in a trivial way:

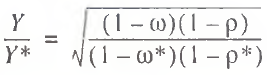                                                                       (27)

The formulas for k and m coefficients estimated by the quadratic method coincide with (22) and (23).

Now let us assess in brief the advantages of determinist methods as compared with econometric techniques.

Determinist methods need no special processing of statistical arrays. Available data for each accounting period are sufficient for estimating potential GDP. Econometric techniques, on the contrary, require the modelling of regression dependences with the statistical estimation of relevant parameters. The latter are averaging values for a long period, and their use may lead to serious errors. Moreover, econometric techniques can only be applied to quite long time series, whereas determinist methods allow estimates to be made of any “single” date (year) irrespective of prior economic dynamics.

Additional technical problems may arise in the econometric estimation of potential GDP, owing to the presence of negative parameters (for example, α and β), which should be positive for general economic reasons. In this case, applied estimates fall within the ambit of pure econometric calculations, allowing the selection of the most suitable method for data smoothing of statistical arrays.

Therefore, determinist procedures are essentially point methods, while econometric techniques can be defined as “interval” methods. The former prove to be, first, much simpler in computational terms and, second, produce more reliable results.

It is notable that the relative ratio of optimal GDP can be estimated by formula (27), by drawing solely on the rates of labor and capital underutilization. This example clearly demonstrates the advantages of determinist methods with regard to ease of calculation. Nonetheless, in our opinion, the linear method is more preferable than the quadratic one, both theoretically and from the practical point of view.

Results of calculations

Considering the above, linear, methods (formulas (21) and (34)) were selected to verify our approaches on actual data by following two scenarios, for elastic and inelastic macrofactors. As applied to the Russian economy, the natural rate of unemployment was estimated at 3% and the normal production capacity underutilization rate, at 10%.

The statistic base necessary and sufficient for relevant calculations is given in Tables 1 and 2; the results of our estimates are shown in Table 3.

Table 1. Production output and macrofactors in the Russian economy

* The number of unemployed is estimated according to the 11.0 methods.

* * These estimates are made by the present author using extrapolation techniques.

Table 2. Underutilization rales of macrofactors in the Russian economy

* Underutilization rates of production capacities were calculated by A. A. Vodyanov, who kindly placed his estimates at the disposal of this author.

Table 3. Estimates of Russia’s potential GDP

A comparison of two scenarios for estimating the potential GDP allows us to classify the first scenario, assuming a high elasticity of two macrofactors, as an optimistic estimation of shifts in the Russian economy. Under this scenario, the potential GDP in 1996 decreased by only 4.8% against the 1989 level. This suggests that, despite a slump in production, Russia still disposes of quite vast standby resources that could be promptly put into operation given improved market conditions. In other words, according to this scenario, the crisis in Russia affected primarily the scope of utilization of its productive potential, the latter itself remaining almost unchanged. If labor promptly adapts to the increasing load on fixed capital, the Russian economy will be able to reach the 1989 level within two to three years under favorable conditions.

An absolutely different picture emerges from the second scenario, based on the rigid adjustment of labor to capital stocks. According to this scenario, labor is a factor limiting the potential growth of GDP, being relatively scarce against the background of obvious overaccumulation of capital. Our estimates show that the growth of employment up to its natural rate increases the utilization rate of production capacities by 1.5% on average, which is of minor significance for domestic production. As a result, potential GDP in 1996 decreased by almost 40% against the 1989 level. If labor fails, at the stage of overcoming the crisis, to provide more intensive “services” in the operation of capital stocks than in 1996, it will take almost a decade to reach the precrisis level in the Russian economy. The situation may still take a turn for the worse, assuming that a major part of currently idle capacities are dead assets, which could hardly be ever used in production.

Regrettably, we have no objective and quite reliable criteria today to be applied to the choice of either scenario for estimating potential GDP. Yet we feel that there are still more arguments in favor of the pessimistic approach. To all appearances, this case is no exception and the truth can be found somewhere in the middle. Therefore, we offer an additional stage in potential GDP estimation, which involves the averaging of results obtained by using both methods. In this case, the sought–for statistical array will look as follows:

These averaged estimates suggest that it will take a long time to overcome the current crisis in Russia, since the breakthrough for the 1989 level will require not only to intensify the commitment of available resources to production operations, but also enlarge the resources themselves and simultaneously raise the efficiency of their utilization.

In this respect, the following additional observation is worthy of note. In the reduced scope of commitment to production, capital proved to be the most flexible, whereas labor poorly adapted to crisis phenomena. At the same time, the actually used capital potential showed, albeit slowly and inexplicitly, a growth of its efficiency, whereas labor productivity was steadily falling (Table 2). So, the market relations have, first and foremost, tightened the demands on capital. Now the time has come for raising the labor efficiency as a basis for surmounting the current crisis. It may be presumed that this will involve the retraining of labor and the placement of more exacting demands on vocational competence.

Methodological conclusions

This analysis makes it possible to formulate several major methodological theses on potential GDP estimation.

First, the current econometric methods of estimating the potential GDP are too rough and biased owing to their failure to take into account two key aspects: the possibility of increasing the utilization of several macrofactors simultaneously and the impossibility of drastically violating the fixed balance between them. Therefore, we have put forward a general econometric approach (formulas (14) and (15), which eliminates these shortcomings.

Second, econometric methods of estimating potential GDP, even if workable, are ineffectual, while their wide use is due primarily to scientific traditions. Their inefficiency arises from, at least, three computational aspects: the inaccuracies and the averaging of all parameters; technical complexities arising in calculations, namely, the need for adequate software and statistical significance tests in all parameters; and high demands placed on databases. Therefore, it is advisable to turn to determinist principles of estimating potential GDP (for example, to the linear method based on formula (21) or the quadratic method based on formula (26). In this case, all the above shortcomings are automatically eliminated.

Third, the estimation of potential GDP can be used to predict national development, primarily, in economic growth forecasts, which becomes particularly topical at the turning points in national development, e.g., when a country, is crawling out of a crisis. Another applied aspect of major practical importance is due to the fact that such estimates help ascertain the relative redundancy or scarcity of the macrofactors for working out a strategy for their importing or exporting. In our opinion, these aspects in applying the results of estimating the potential GDP in macroeconomic forecasting and state regulation are insufficiently appreciated and need further study. This is apparently one of the most promising research lines in current macroeconomic studies.

Fourth, our analysis shows that the use of synchronous and asynchronous methods for estimating the potential GDP produces qualitatively different results. To remove this discrepancy, we can recommend now to resort to the averaging of results obtained from the two procedures. We see our next task in establishing criteria and algorithms for determining the degree of macrofactors' elasticity in a concrete context, which will provide for the more weighted use of both approaches and their workable combination. It is in this research that the most tangible results can be obtained with a view to generalizing and elaborating the method of estimating the potential GDP.

Fifth, applied calculations of Russia’s potential GDP indicate that it will take no less than seven to eight years for our economy to reach the precrisis level in domestic production even under the most favorable conditions. The low level of demand placed on the quality of labor and its efficient management is a factor that aggravates the crisis and prolongs it. The eventual overcoming of this tendency will inevitably intensify the antisocial component in Russia’s economic development.

References

1. MacConnell, K.R. and Brew, S.L.. Economics: Principles, Problems and Politicies (Translated under the title Ekonomika: printsipy, problems i polilika, Moscow: Respublika, 1992, vol. 1.

2. Vodyanov, A.A., Inveslitsionnye protsessy v ekonomike perekhodnogo perioda (melody issledovaniya i prognozimvaniya) (Investment Processes in an Economy in Transition: Methods of Study and Forecasting), Moscow: IMEI, 1995.

Official link to the article:

Balatskii E.V. Estimating Potential GDP// «Studies on Russian Economic Development», Vol.11. No.1. 2000, pp.11–17.